这个问题源于某个微信群的讨论,若干个精益六西格玛业内大咖对此展开了激烈的讨论。其说法来自于一个共识,即当检验的差一定时,随着样本量的增大,这个差异是一定可以检验出来的。但问题就在于这个差是否一定,因为样本均值是一个变量,如果原假设成立,则p值不但不会随着样板量增大而变小,反而会增大。当然如果原假设不成立,则p值应该是会变小的。
实际情况到底如何呢,这引起了我的兴趣。起初我设想运用R或者Python之类的软件做大量的仿真实验,看看p值到底如何变化,但无奈目前编程还是我难以逾越的门槛。经过一段时间摸索,我用大家熟知的软件做了一些摸索,得出了一些结论,用两篇文章分享出来,希望得到大家的批评指正。
实验设计
以单样本单侧检验为例做实验,分别生成样本量为10、15、20、…、100的均值为10,标准差为0.2的正态分布样本各500个。
实验1
实验的假设为:H0:μ=10 ,Ha:μ<10。
以此假设计算t值和p值,用图形来查看p值随样板量增大的变化趋势。
初步猜想,因为生成的样本均值与假设均值相同,即原假设应该是成立的,因此随着样本量的增大,样本的均值应该越接近假设均值10,则p值也应该随之增大,且越来越接近0.5(样本均值与假设均值完全重合时,p值为0.5)。
实验2
实验的假设为:H0:μ=10.1,Ha:μ<10.1。
这是一个比较小的差,为生成样本标准差的0.2一半。初步猜想,在样板量较小时,会有比较多的检验无法拒绝原假设,但随着样板量增大,p值会变小,直至绝大多数样本都能够拒绝原假设。
取功效为0.9,可以算出最小样本量为36,因此实验取10~100的样本量是恰当的。
实验结果
实验1
首先看看箱线图。
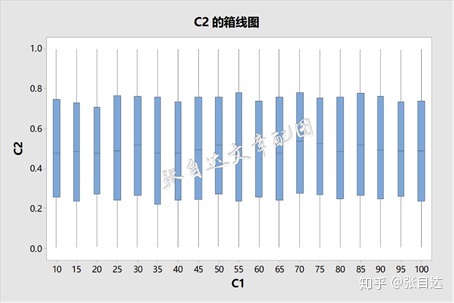
奇怪,看起来不同的样本量p值没有多大差异,而且中位数在0.5附近波动。用区间图可以看得更清楚一些。
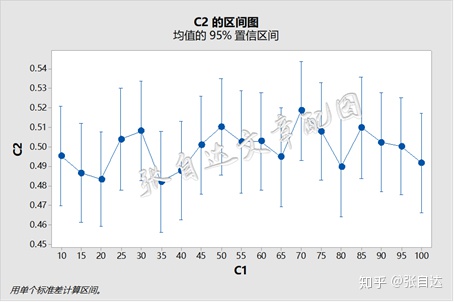
看起来p值的均值在0.5附近波动,置信区间很小且重叠,可以说p值与样本量无关。
看看p值的分布,非常接近均匀分布。

这个结果与实验前预想的不同,也出乎我的意料,但细想起来这个结果反而是必然的。
我们在做比较分析之前,总是要设定误判所要承担的风险,即α风险。也就是说,即使原假设成立,但是我们还是有少量的概率(α)抽到可以拒绝原假设的样本的。在只进行一次抽样时,α风险确实是个小概率,但当抽样次数增多时,这个概率就会变得很大了。熟悉二项分布的同仁很快就可以列出k次抽样至少有一次误判的概率计算公式
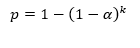
根据这个公式,2次抽样至少有一次误判的概率为0.0975,10次抽样这个概率就变为0.401。因此无论样本量有多大,多次抽样后总会有比较大的概率出现误判的。
取α=0.05,不同样本量下检验的误判率可见下图。

这张图告诉我们,不管样本量有多大,在原假设成立时,大约会有5%(α的取值)次抽样会出现误判。
这又引出另外一个话题,如果一次比较分析得出的p值是0.001,那么我们承担的误判风险到底是多少呢?有很多同仁认为风险就是0.001,但通过上面的实验,我还是认为风险仍为α,这在吕小康老师的论文《Fisher与Neyman-Pearson的分歧与心理统计中的假设检验争议》有专门的论述。
实验2
在均值确实有差异时,实验的结果与预想的差不多,请看下图。
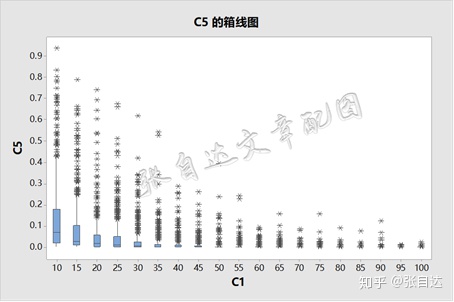

显然,随着样本量的增加,p值逐渐向0靠近。
拒绝的概率也会随着样本量的增加逐渐提高到100%,见下图。
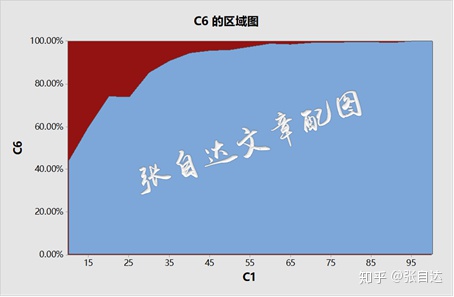
上图红色区域就是漏检率,也就是β风险。可见样本量对检验功效(1-β)的影响,样本量的增大会提高检验的功效。
上面的实验每次增加样本量时都是重新抽样,实操中还大量存在补充抽样的情况,即在现有样本的条件下补充抽一部分样,合在一起成为新的样本进行新的检验。
为此对实验进行重新设计,从样本量10开始,每次补充抽5个样,形成新的样本进行检验。
实验1的结果如下:
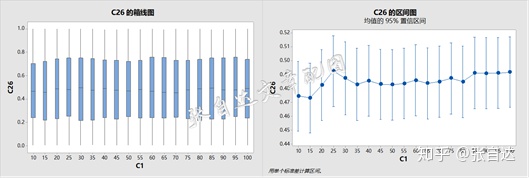
可以看出,p值变化不大,置信区间也都包含0.5,说明在原假设成立的条件下,不同的样本量检验结果没有显著的差异。当然这有一个很重要的前提,就是假设忽略抽样时间的影响,即过程稳定,没有发生特殊原因造成的变异。如果这个假设不成立,那么这个结论就不一定成立了。
补充抽样下检验的结果会发生一些变化,但是这个变化不大,属于正常波动。具体变化情况如下图:

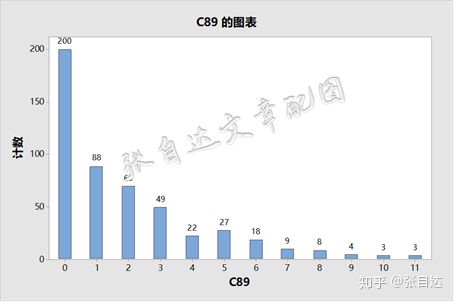
具体到每个样本的变化,可以用下图表示:
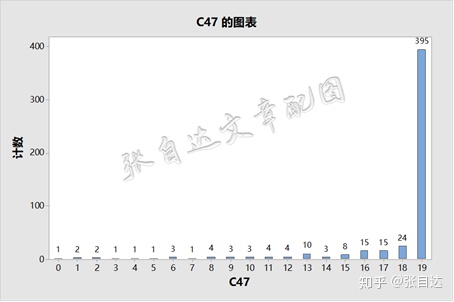
其中0表示19次检验都拒绝,只有1个样本如此。19表示19次检验都不拒绝,这种情况占总样本比例达到79%,在原假设成立的条件下,这是必然的结果。而中间的数字则表明有拒绝也有不拒绝,说明不同的样本量下检验的结果不同。如10次不拒绝、9次拒绝的样本有3个。
实验2的结果也不出乎意料,见下图。
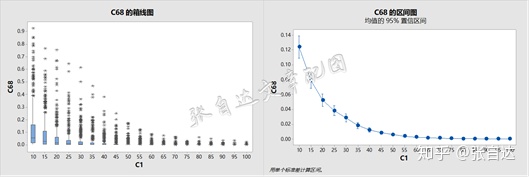
这个结果与前面重新抽样的结果差不多,在原假设不成立时,样本量越大,p值越小。
拒绝率随着样本量的增加不断在增大,直到100%拒绝。

具体到单个样本,从下图可以看出,没有一直不拒绝的样本,而一直都拒绝的样本只占到40%,说明随着样本量的增大,原来不拒绝的样本全部变成了拒绝。
这个仿真实验告诉我们以下几个结论:
1. 原假设为真时,检验的结果与样本量关系不大,当然样本量太少也让人不太放心,所以不能拿几个样检验一下就是无法拒绝原假设。
2. 多次抽样检验会有约α的概率出现误判,因此只有一次抽样时,不管p值是多少,我们承担的误判风险总是α。
3. 如果原假设不成立,那么随着样本量的增加,拒绝原假设的概率也大大增加,直至100%拒绝。
4. 如果原假设不成立,当样本量较小时,会有比较大的漏判概率,样本量增大会减少漏检概率,这也是在检验之前需要估计样本量的原因,这样既可以保证检验功效,又能尽可能控制检验成本。
以上结论的前提是生产过程稳定,没有发生异常波动,否则结论可能不够可靠。
看到这里,可能有人会产生一个疑问:很多时候并不知道实际的差异,应该如何确定检验的差异呢?这个问题我也不是很清楚,下一篇再来谈谈我的粗浅认识。
请关注我的微信公众号:张老师漫谈六西格玛