道格拉斯矢量曲线抽稀算法C#语言非递归实现

1. 道格拉斯-普克算法简介

道格拉斯-普克算法(Douglas–Peucker algorithm，亦称为拉默-道格拉斯-普克算法、迭代适应点算法、分裂与合并算法)是将曲线近似表示为一系列点，并减少点的数量的一种算法。该算法的原始类型分别由乌尔斯·拉默（Urs Ramer）于1972年以及大卫·道格拉斯（David Douglas）和托马斯·普克（Thomas Peucker）于1973年提出，并在之后的数十年中由其他学者予以完善。

经典的Douglas-Peucker算法描述如下：

1. 在曲线首尾两点A，B之间连接一条直线AB，该直线为曲线的弦；
2. 得到曲线上离该直线段距离最大的点C，计算其与AB的距离d；
3. 比较该距离与预先给定的阈值threshold的大小，如果小于threshold，则该直线段作为曲线的近似，该段曲线处理完毕。
4. 如果距离大于阈值，则用C将曲线分为两段AC和BC，并分别对两段取信进行1~3的处理。
5. 当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即可以作为曲线的近似。

由上述可见，道格拉斯-普克算法是一种过程递归的算法。在实际使用道格拉斯抽稀算法时，使用递归会使得在递归过程中存在大量的临时变量。现参考吴铭杰¹论文中的非递归方式实现道格拉斯抽稀算法。该方法简单实用，容易编写代码，具有较高的安全性。

2. C#语言非递归实现

下面给出该算法的C#语言非递归实现，所用到的类方法均使用静态方法以减少开销提高效率：
其中SeriesPoint类型为System.Windows.Point的类化；DataSeries类型为SeriesPoint集合的封装(实现IEnumerable和ICollection<>接口)。

// 道格拉斯抽稀算法
public static DataSeries DouglasThinningMachine(DataSeries seriesPoints)
{
	if (seriesPoints == null)
	{
		throw new ArgumentNullException(nameof(seriesPoints));
	}
	List<SeriesPoint> spList = seriesPoints.series;
	int max = spList.Count;
	if (max < 500)
	{
		return seriesPoints;
	}
	// 此处限定了距离阈值
	double threshold = 10;
	int location = 0;
	// 创建两个栈记录索引值
	Stack<int> A = new Stack<int>();
	Stack<int> B = new Stack<int>();
	A.Push(0);
	B.Push(max - 1);
	do
	{
		var d = FindMostDistance(spList, A.Peek(), B.Peek(), ref location);
		if (d > threshold)
		{
			B.Push(location);
		}
		else
		{
			A.Push(location);
			B.Pop();
		}
	} while (B.Count > 0);
	List<int> listOfIndex = A.ToList();
	listOfIndex.Sort();
	DataSeries result = new DataSeries();
	foreach (int index in listOfIndex)
	{
		result.Add(spList[index].Clone());
	}
	return result;
}
// 计算最大距离
private static double FindMostDistance(List<SeriesPoint> seriesPoints,int start,int end,ref int location)
{
	if (end - start <= 1)
	{
		location = end;
		return 0;
	}
	double result = 0;
	SeriesPoint startPoint = seriesPoints[start];
	SeriesPoint endPoint = seriesPoints[end];
	for (int i = start + 1; i < end; i++)
	{
		// 调用 MathUtil Class 中的静态方法GetDistanceToLine
		var d = MathUtil.GetDistanceToLine(startPoint, endPoint, seriesPoints[i]);
		if (d > result)
		{
			result = d;
			location = i;
		}
	}
	return result;
}

// 在 MathUtil Class 中

public static double GetDistanceToLine(double p1x, double p1y, double p2x, double p2y, double refpx, double refpy) 
	=> Math.Abs(((p2y - p1y) * (refpx - p1x)) - ((refpy - p1y) * (p2x - p1x))) / Math.Pow(((p2y - p1y) * (p2y - p1y)) + ((p2x - p1x) * (p2x - p1x)), 0.5);

public static double GetDistanceToLine(Point point1, Point point2, Point refPoint) 
	=> MathUtil.GetDistanceToLine(point1.X, point1.Y, point2.X, point2.Y, refPoint.X, refPoint.Y);

public static double GetDistanceToLine(SeriesPoint point1, SeriesPoint point2, SeriesPoint refPoint)
	=> MathUtil.GetDistanceToLine(point1.X, point1.Y, point2.X, point2.Y, refPoint.X, refPoint.Y);

3. 抽稀算法测试与结果对比

通过Random类构造一些带有一定规律的数据点共1000个，使用抽稀算法(阈值为10)后保留点数430个，算法用时约4毫秒。现取前100个样本值作为对比观察：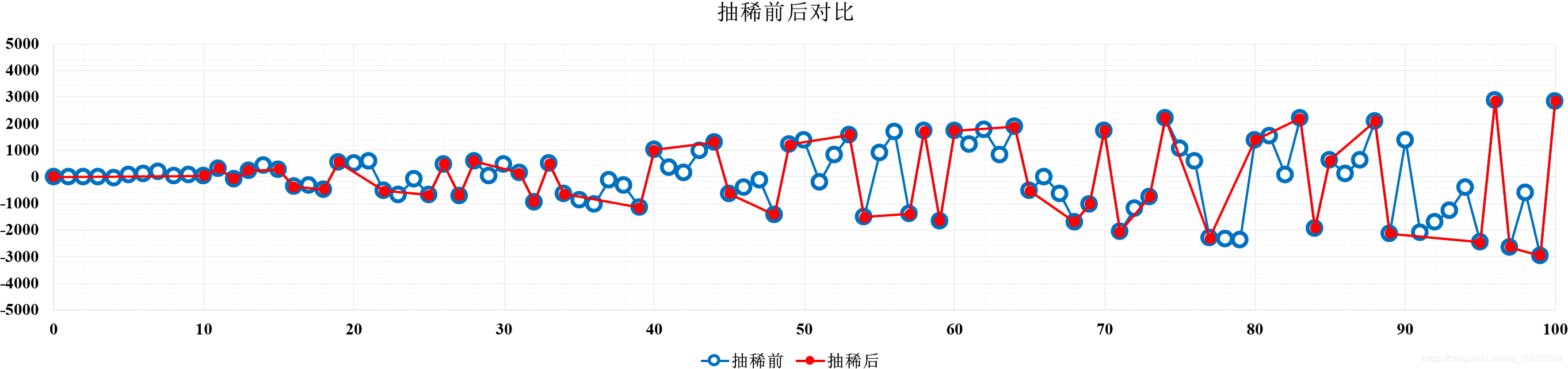

由图可见，该算法具有较好的抽稀效果。

参考文献