搜索

BFS

常用于求最小值
基于迭代，相较于 $D FS$ 不容易爆栈。

Flood Fill 模型

顾名思义洪水覆盖问题。

可以在线性时间复杂度内找到矩阵内某个点所在的连通块。

可以维护所有矩阵内连通块的个数

typedef pair<int, int> pii;
int n, m;            //矩阵的长和宽
int vis[MAXN][MAXN]; //标记每个点属于哪一个连通块，0表示还问访问过
int mp[MAXN][MAXN];  //每个点的权值
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
int cnt = 0;    //连通块个数
int size[MAXN]; //连通块内部元素个数
void bfs(int x, int y) {
    queue<pii> q;
    vis[x][y] = cnt;
    q.push({x, y});
    while (q.size()) {
        int x = q.front().first, y = q.front().second;
        q.pop();
        num++; //连通块内部个数加一
        for (int i = 0; i < 4; i++) {
            int xx = x + dx[i], yy = y + dy[i];
            if (vis[xx][yy] != 0)
                continue; //之前已访问过
            if (xx > n || xx < 1 || yy > m || yy < 1)
                continue; //越界
            if (mp[x][y] != mp[xx][yy])
                continue; //权值不同
            vis[xx][yy] = cnt;
            q.push({xx, yy});
        }
    }
    size[cnt] = num;
}

void solve() {
    cin >> n >> m;
    //输入点权
    for (int i = 1; i <= n; i++)
        for (int i = 1; i <= m; i++)
            if (!vis[i][j]) //发现了一个未搜索过的连通块
                cnt++, bfs(x, j);
}

求连通块个数

最基本的模板题，注意输入字符串的处理。

int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
char s[MAXN][MAXN];
int vis[MAXN][MAXN];
ll n, m;
int cnt = 0;
typedef pair<int, int> pii;
void bfs(int x, int y) {
    queue<pii> q;
    vis[x][y] = 1;
    q.push({x, y});
    while (q.size()) {
        int x = q.front().first, y = q.front().second;
        q.pop();
        for (int i = 0; i < 8; i++) {
            int xx, yy;
            xx = x + dx[i];
            yy = y + dy[i];
            if (vis[xx][yy])
                continue;
            if (s[xx][yy] == '.')
                continue;
            if (xx > n || xx < 1 || yy > m || yy < 1)
                continue;
            vis[xx][yy] = 1;
            q.push({xx, yy});
        }
    }
}
void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> s[i] + 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (!vis[i][j] && s[i][j] == 'W') {
                cnt++;
                bfs(i, j);
            }
        }
    }
    cout << cnt << endl;
}

状态压缩+统计最大连通块个数

其他与模板内容基本一致，区别就在于判断连通性这一块。题目将原本上下左右的四种状态通过二进制压缩成了一维。那么在判断连通性的时候还得判断这一维上是否有障碍物阻挡了连通性。

左边连通，二进制第 $1$ 位为 $0$
上边连通，二进制第 $2$ 位为 $0$
右边连通，二进制第 $3$ 位为 $0$
下边连通，二进制第 $4$ 位为 $0$

为了满足状态压缩的条件， $d x$ 和 $d y$ 数组的顺序必须一一对应其状态。

这题还有比较恶心的是选取的坐标系不同。以往都是以坐标原点为中心，但这次得以某个点为中心，所以上下左右和以往的表示不太一样，得完全反过来看。

int n, m, cnt, ans;
int dx[4] = {0, -1, 0, 1};
int dy[4] = {-1, 0, 1, 0};
int vis[MAXN][MAXN];
int mp[MAXN][MAXN]; //放大小

void bfs(int x, int y) {
    int num = 0;
    vis[x][y] = cnt;
    queue<pii> q;
    q.push({x, y});
    while (q.size()) {
        num++;
        int x = q.front().first, y = q.front().second;
        q.pop();
        int val = mp[x][y];
        for (int i = 0; i < 4; i++) {
            int xx = x + dx[i], yy = y + dy[i];
            if (vis[xx][yy] != 0)
                continue;
            if (((val >> i) & 1))
                continue;
            if (xx > n || xx < 1 || yy > m || yy < 1)
                continue;
            vis[xx][yy] = cnt;
            q.push({xx, yy});
        }
    }
    ans = max(ans, num);
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> mp[i][j];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (!vis[i][j]) {
                cnt++;
                bfs(i, j);
            }
        }
    }
    cout << cnt << endl;
    cout << ans << endl;
}

整体法判断连通块状态

我们考虑把连通块看做一个点。那么如果这个连通块是山谷，那么他的权值小于其他所有邻点的权值；如果这个连通块是山峰，那么他的权值大于其他所有邻点的权值。

考虑在连通块内部定义两种状态，是否可能成为山峰和是否可能成为山谷，一开始都默认为是。当遍历到一个邻点大于连通块的权值，山峰置为不可能；当遍历到一个邻点小于连通块的权值，山谷置为不可能。

遍历完整个连通块后再对这两个状态进行判断即可。

int mp[MAXN][MAXN], vis[MAXN][MAXN];
int n;
int dx[8] = {-1, -1, -1, 0, 0, 1, 1, 1};
int dy[8] = {-1, 0, 1, -1, 1, -1, 0, 1};
int sum1, sum2; //山峰和山谷个数

void bfs(int x, int y) {
    vis[x][y] = 1;
    int f1 = 1; //是否有可能成为山峰
    int f2 = 1; //是否有可能成为山谷
    queue<pii> q;
    q.push({x, y});
    while (q.size()) {
        int x = q.front().first, y = q.front().second;
        q.pop();
        for (int i = 0; i < 8; i++) {
            int xx = x + dx[i], yy = y + dy[i];

            if (xx > n || xx < 1 || yy > n || yy < 1)
                continue;
            if (mp[xx][yy] > mp[x][y]) {
                //不可能成为山峰了 
                f1 = 0;
                continue;
            }
            if (mp[xx][yy] < mp[x][y]) {
                //不可能成为山谷了
                f2 = 0;
                continue;
            }
            if (vis[xx][yy])
                continue;
            if (mp[xx][yy] == mp[x][y]) {
                vis[xx][yy] = 1;
                q.push({xx, yy});
            }
        }
    }
    if (f1) {
        sum1++;
        // cout<<"top: "<<x<<" "<<y<<endl;
    }
    if (f2) {
        sum2++;
        // cout<<"bottom: "<<x<<" "<<y<<endl;
    }
}

void solve() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> mp[i][j];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (!vis[i][j])
                bfs(i, j);
    cout << sum1 << " " << sum2 << endl;
}

最短路模型

$BFS$ 相当于层次遍历，从当前点出发，遍历到的点都是下一个层次的点。

最短路问题下，如果边权相同，答案就相当于求的是层次最少的方案。可以通过 $BFS$ 解决。

int n, m; //矩阵长宽
typedef pair<int, int> pii;
int sx, sy, ex, ey;  //起点和终点的坐标
int dis[MAXN][MAXN]; //起点到 (i,j) 的最短距离
int mp[MAXN][MAXN];  // 1表示有障碍物无法通过
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
#define INF 0x3f3f3f3f

int bfs(int sx, int sy) {
    queue<pii> q;
    q.push({sx, sy});
    while (q.size()) {
        int x = q.front().first, y = q.front().second;
        q.pop();
        if (x == sx && y == sy)
            return dis[x][y]; //遍历到了终点
        for (int i = 0; i < 4; i++) {
            int xx = x + dx[i], yy = y + dy[i];
            if (xx > n || xx < 1 || yy > m || yy < 1)
                continue; //越界
            if (dis[xx][yy] <= dis[x][y] + 1)
                continue; //其实没必要这么写，dis当vis用
            if (mp[xx][yy])
                continue; //有障碍物
            dis[xx][yy] = dis[x][y] + 1;
            q.push({xx, yy});
        }
    }
}

void init() {
    memset(dis, 0x3f, sizeof dis);
    dis[sx][sy] = 0;
}

模板题

int n, m;
int dx[8] = {-2, -2, -1, -1, 1, 1, 2, 2};
int dy[8] = {-1, 1, -2, 2, -2, 2, -1, 1};
char s[MAXN][MAXN];
int dis[MAXN][MAXN];
bool ok(int x, int y) {
    if (x > n || x < 1 || y > m || y < 1)
        return false;
    return true;
}

int bfs(pii se) {
    queue<pii> q;
    q.push(se);
    while (q.size()) {
        int x = q.front().first, y = q.front().second;
        q.pop();
        for (int i = 0; i < 8; i++) {
            int xx = x + dx[i], yy = y + dy[i];
            if (!ok(xx, yy))
                continue;
            if (dis[xx][yy] <= dis[x][y] + 1)
                continue;
            if (s[xx][yy] == '*')
                continue;
            dis[xx][yy] = dis[x][y] + 1;
            q.push({xx, yy});
            if (s[xx][yy] == 'H')
                return dis[xx][yy];
        }
    }
}

void solve() {
    cin >> m >> n;
    for (int i = 1; i <= n; i++) {
        cin >> s[i] + 1;
    }
    pii se;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (s[i][j] == 'K')
                se = {i, j}, dis[i][j] = 0;
            else
                dis[i][j] = INF;
        }
    }
    cout << bfs(se);
}

多源BFS

可以理解为有 多个起始状态 的其他最短路基本模型，这些起始状态全部等价。

在这种具有多个等价的起始状态问题中，我们只需要在 $BFS$ 开始前 把这些起始状态全部插入队列 ，根据 $BFS$ 逐层搜索的性质， $BFS$ 的过程就相当于每个起点先扩展 $1$ 层，再扩展 $2$ 层， $3$ 层，以此类推。

其实可以理解成超级源点的题目

模板

求出每个点距离权值为 $1$ 的点的最小曼哈顿距离。

将所有权值为 $1$ 的点推入队列再求层数即可，在这里曼哈顿距离等价于层数。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define MAXN 1005
typedef pair<int, int> pii;
#define INF 0x3f3f3f3f
int n, m;
char s[MAXN][MAXN];
int dis[MAXN][MAXN];
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};
bool ok(int x, int y) {
    if (x > n || x < 1 || y > m || y < 1)
        return false;
    return true;
}

void bfs() {
    queue<pii> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (s[i][j] == '1')
                q.push({i, j}), dis[i][j] = 0;
    while (q.size()) {
        int x = q.front().first, y = q.front().second;
        q.pop();
        for (int i = 0; i < 4; i++) {
            int xx = x + dx[i], yy = y + dy[i];
            if (!ok(xx, yy))
                continue;
            if (dis[x][y] + 1 >= dis[xx][yy])
                continue;
            dis[xx][yy] = dis[x][y] + 1;
            q.push({xx, yy});
        }
    }
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> s[i] + 1;
    memset(dis, 0x3f, sizeof dis);
    bfs();
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cout << dis[i][j] << " ";
        }
        cout << endl;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}

题意：

给出一棵树，你要从根节点移动到叶子节点，每次只能移动一下。在树中的其他节点会有敌人，他们会来拦截你，每次他们也只能移动一下。问到最后能否逃到任意一个叶子节点。

把所有敌人敌人推入队列，求一遍 $BFS$ ；把根节点推入队列，求一遍 $BFS$ 。如果在某个节点第一遍的结果小于等于第二遍的结果，说明敌人可以在这里逮住你，必须避开这条路。如果能找到一个叶子节点，使得第一遍的最短路大于第二遍的最短路，说明可以到达这个叶子节点。

画蛇添足用了优先队列，第二问的时候才想清楚这个道理

int n, k, a[MAXN];
int head[MAXN];
int tot;
int isleaf[MAXN];
int d[MAXN], vis[MAXN]; // 0表示未访问，2表示自己可以走，1表示不能走
struct EDGE {
    int to, next;
} edge[MAXM];
void add_edge(int from, int to) {
    edge[++tot].to = to;
    edge[tot].next = head[from];
    head[from] = tot;
}

void init() {
    tot = 0;
    memset(head, 0, sizeof(head));
    memset(d, 0, sizeof(d));
    memset(vis, 0, sizeof(vis));
}

void solve() {
    init();
    cin >> n >> k;
    for (int i = 1; i <= k; i++) {
        cin >> a[i];
        vis[a[i]] = 1;
    }
    vis[1] = 2;
    for (int i = 1; i < n; i++) {
        int u, v;
        cin >> u >> v;
        add_edge(u, v), add_edge(v, u);
        d[u]++, d[v]++;
    }
    for (int i = 1; i <= n; i++) {
        if (d[i] == 1 && i != 1)
            isleaf[i] = 1;
        else
            isleaf[i] = 0;
    }
    priority_queue<pii, vector<pii>, greater<pii>> q;
    //时间，类型（敌人为1自己为2），位置
    q.push({{0, 2}, 1});
    for (int i = 1; i <= k; i++)
        q.push({{0, 1}, a[i]});
    while (!q.empty()) {
        int tim = q.top().first.first;
        int type = q.top().first.second;
        int now = q.top().second;
        q.pop();
        for (int i = head[now]; i; i = edge[i].next) {
            int to = edge[i].to;
            if (!vis[to]) {
                vis[to] = type;
                q.push({{tim + 1, type}, to});
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        if (isleaf[i] && vis[i] == 2) {
            cout << "YES" << endl;
            return;
        }
    }
    cout << "NO" << endl;
}

最小步数（状态转移）模型

不同于之前的局部求解。状态转移模型（如八数码）一般将给出一个集合，给出一些可行的操作，问将这个集合转化为另一个集合所需的最小操作数量。

在具体操作时将开始的结果用哈希表示，也就是把整个集合看做一个整体。状态的扩展也用哈希值之间的转化来完成。当哈希值与终点的哈希值相匹配时就终止程序。

利用 $u n or d ere d ma p$ 可以代替手写哈希的步骤。

题意

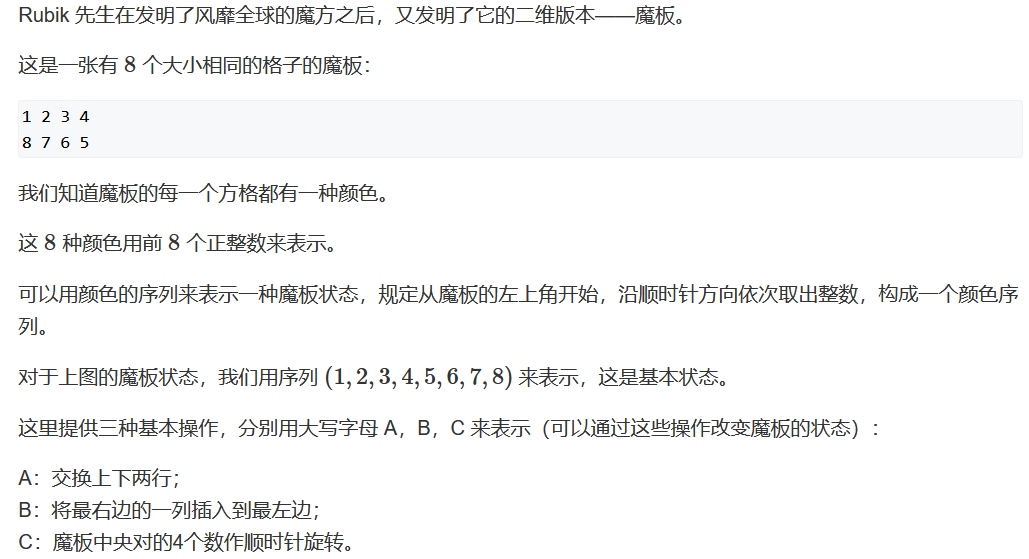
首先明确将所有状态用哈希值表示。

声明一个哈希表，用于存放从起点状态到当前状态的最小步数

声明一个哈希表，用于存放当前状态的前驱，包含前驱串和操作步骤。

输出结束状态的最小步数，再根据前驱倒着遍历回起点记录操作步骤，倒转后输出。

unordered_map<string, int> dis;
unordered_map<string, pair<char, string>> pre; //前驱节点
string s, e;

string get1(string s) {
    reverse(s.begin(), s.end());
    return s;
}

string get2(string s) {
    string ans = "";
    ans += s[3], ans += s[0], ans += s[1], ans += s[2], ans += s[5], ans += s[6], ans += s[7], ans += s[4];
    return ans;
}

string get3(string s) {
    string ans = "";
    ans += s[0], ans += s[6], ans += s[1], ans += s[3], ans += s[4], ans += s[2], ans += s[5], ans += s[7];
    return ans;
}

void bfs(string s) {
    dis[s] = 0;
    if (s == e)
        return;
    queue<string> q;
    q.push(s);
    while (q.size()) {
        string now = q.front();
        q.pop();
        if (now == e)
            return;
        string s1 = get1(now);
        string s2 = get2(now);
        string s3 = get3(now);
        if (dis.count(s1) == 0) {
            pre[s1] = {'A', now};
            dis[s1] = dis[now] + 1;
            q.push(s1);
        }
        if (dis.count(s2) == 0) {
            pre[s2] = {'B', now};
            dis[s2] = dis[now] + 1;
            q.push(s2);
        }
        if (dis.count(s3) == 0) {
            pre[s3] = {'C', now};
            dis[s3] = dis[now] + 1;
            q.push(s3);
        }
    }
}

void solve() {
    s = "12345678";
    for (int i = 1; i <= 8; i++) {
        int tmp;
        cin >> tmp;
        e += '0' + tmp;
    }
    bfs(s);
    cout << dis[e] << endl;
    string ans = "";
    while (e != s) {
        // cout<<pre[e].first<<endl;
        ans += pre[e].first;
        e = pre[e].second;
    }
    // cout<<ans<<endl;
    reverse(ans.begin(), ans.end());
    cout << ans;
}

双端队列BFS

其实是和优先队列一个道理，不同的点 优先级 不同。只不过双端队列只能解决两种状态，也就是两种优先级；而优先队列重载完运算符就可以随便操作了，例如堆优化最短路。

例题：

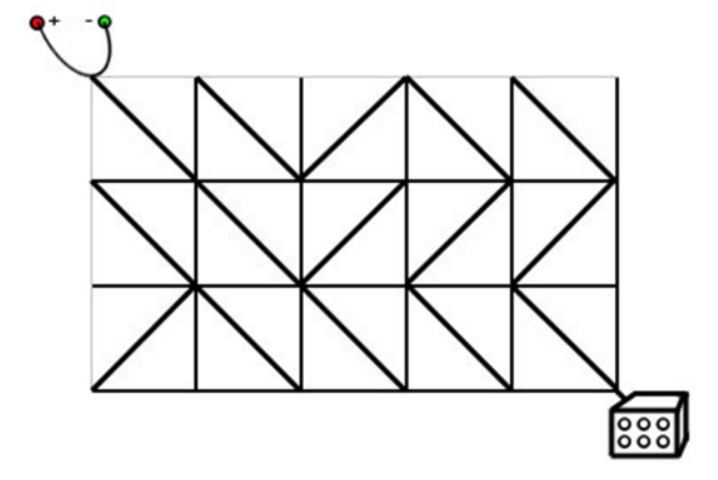
所有电线都是斜着摆放的。可以转动任意电线。问最少需要转动几根电线才能从 $(0, 0)$ 走到 $(n, m)$ 。

首先可以证明坐标和为奇数的点永远无法到达。因为电线只能斜着摆放，最初状态又是从 $(0, 0)$ 这个偶点传递过来的。

所以电线摆好后只有一种状态，即不会要求某根电线在某条回路上摆的是 $1$ 方向，而在另一条回路上摆的是 $2$ 方向，证明了题目的合法性。

如果两点之间本来就有边相连，相当于边权为 $0$ ，否则边权为 $1$ 。题目就转化成了 $BFS$ 求最短路问题。

边权为 $0$ 的优先级比边权为 $1$ 的优先级高，所以边权为 $0$ 推入队首，边权为 $1$ 推入队尾。

输入过于阴间，直接开抄别人的处理方法。

char mp[MAXN][MAXN];
int dis[MAXN][MAXN];
int vis[MAXN][MAXN];
int n, m;
char cs[] = "\\/\\/";
int dx[4] = {-1, -1, 1, 1}, dy[4] = {-1, 1, 1, -1};
int ix[4] = {-1, -1, 0, 0}, iy[4] = {-1, 0, 0, -1};
int bfs() {
    deque<pii> q;
    memset(dis, 0x3f, sizeof dis);
    memset(vis, 0, sizeof vis);
    dis[0][0] = 0;
    q.push_front({0, 0});
    while (q.size()) {
        int x = q.front().first, y = q.front().second;
        q.pop_front();
        if (vis[x][y])
            continue;
        vis[x][y] = 1;
        for (int i = 0; i < 4; i++) {

            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a > n || b < 0 || b > m)
                continue;

            int xx = x + ix[i], yy = y + iy[i];
            int d = dis[x][y] + (mp[xx][yy] != cs[i]);

            if (d < dis[a][b]) {
                dis[a][b] = d;

                if (mp[xx][yy] != cs[i])
                    q.push_back({a, b});
                else
                    q.push_front({a, b});
            }
        }
    }
    return dis[n][m];
}

void solve() {
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        cin >> mp[i];
    int ans = INF;
    ans = bfs();
    if (ans == INF)
        cout << "NO SOLUTION" << endl;
    else
        cout << ans << endl;
}

双向广搜

当状态非常庞大时，单向搜索要么爆空间要么会超时。这时可以考虑同时从起点和终点往中间搜。

假设之前的时间复杂度为 $10^6$ ，双向广搜优化后时间复杂度就能降为 $\times 10^3$ ，可以看出来优化非常明显。

这么好用的东西之前没听说过肯定是因为适用性非常窄。最短路模型和连通块都用不了，基本上只能用于优化最小步数模型。

给出具体题目来方便理解。

定义两个队列，分别表示从起点开始扩展的状态和从终点开始扩展的状态。

定义两个哈希表，分别表示起点到某个状态所需的最小步数和终点到某个状态所需的最小步数。

每次选取起点一方和终点一方状态较少的一方并且只扩展一层，如果扩展的过程中发现某个状态在两个地方都出现过，那么就返回这个点到两端端点的距离之和，这就是以这个点为桥梁，从起点到终点变换所需的步数。否则返回一个非法的值表示没找到，继续扩展状态搜索。

这样第一个找到的桥梁一定能满足这是最少的变换步数，因为两边的层数都是从小到大来扩展状态的。第一个两边共有的状态肯定满足此时两边的层数最小。

题意：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
string A, B;
int n;
string a[10], b[10];             //子串变换规则
unordered_map<string, int> disa; //起点到某个状态的距离
unordered_map<string, int> disb; //终点到某个状态的距离

int extend(queue<string> &q, unordered_map<string, int> &disa, unordered_map<string, int> &disb, string a[], string b[]) {
    //从当前队列仅扩展一层状态
    int len = q.size();
    for (int k = 0; k < len; k++) {
        //保证只扩展一层
        string now = q.front();
        q.pop();
        if (disb.count(now)) //在对面找到了相同状态的点
            return disa[now] + disb[now];
        
        for (int i = 0; i < now.size(); i++) {
            //枚举替换开始位置
            for (int j = 0; j < n; j++) {
                //枚举规则
                if (now.substr(i, a[j].size()) == a[j]) {
                    //能替换
                    string to = now.substr(0, i) + b[j] + now.substr(i + a[j].size()); //扩展状态
                    if (disa.count(to))
                        continue; //之前这个状态已经出现过了
                    disa[to] = disa[now] + 1;
                    q.push(to);
                }
            }
        }
    }
    return 11; //返回一个非法的数，表示没找到
}

int bfs() {
    disa[A] = 0;
    disb[B] = 0;
    queue<string> qa, qb; // qa表示从起点开始搜，qb表示从终点开始搜
    qa.push(A), qb.push(B);
    while (qa.size() && qb.size()) {
        //只有当qa和qb两个队列里都有东西时才能继续搜索
        int t; //从小的队列开始扩展，能否出现另一个队列的元素，如果可以返回合法步数
        if (qa.size() <= qb.size())
            t = extend(qa, disa, disb, a, b);
        else
            t = extend(qb, disb, disa, b, a); //扩展的队列不同，参数位置也不同
        if (t <= 10)
            return t;
    }
    return 100;
}

void solve() {
    cin >> A >> B;
    while (cin >> a[n] >> b[n])
        n++;
    int ans = bfs(); //开始双端搜索
    if (ans > 10)
        cout << "NO ANSWER!" << endl;
    else
        cout << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    solve();
    return 0;
}

A-STAR

做法：

引入一个估值函数，用来估计某个点到达终点的距离。

记 $f$ 是估值函数， $g$ 是真实值，那么 $\leq g(state)$ ，越接近越好（估值为 $0$ 时，类似于迪杰斯特拉算法）

记 $d i s$ 为起点到 $s t a t e$ 状态的步数

利用的是优先队列，排序依据是 $d i s [s t a t e] + f [s t a t e]$

使用前提，保证有解（无解时，仍然会把所有空间搜索，会比一般的bfs慢，因为优先队列的操作时log级别的）

只能保证终点最优解

除了终点，每个状态都有可能被扩展多次（因为无法保证当前是错误的还是正确的）（不用判重，除了终点以外，所有点出来一次再push进去更新一次）

A* 不用判重
以边权都为1为例
A o→o→o
↑ ↓
S o→o→o→o→o→o→o T
B
$ dis[A] = dis[S]+1 + f[A] = 7 $
$ dis[B] = dis[S]+1 + f[B] = 5$
则会优先从 $B$ 这条路走到 $T$
B走到 $T$ 后再从 $A$ 这条路走到 $T$

伪代码

while(q.size()) q为优先队列
{
    now=优先队列队头（小根堆）
    q.pop();
    当终点第一次出队时，break;
    枚举now的所有邻边
    将邻边入队
        权值为起点到当前点的真实距离+当前点到终点的估计距离（启发函数）
        ***估计值小于等于当前点到终点的真实距离
        （核心条件，这样才能保证绝对正确，越接近越好。如果取0就相当于没优化）
}

举个例子，蓝色圈内部表示所有的状态，绿色圈内部表示优化后实际搜索的所有状态

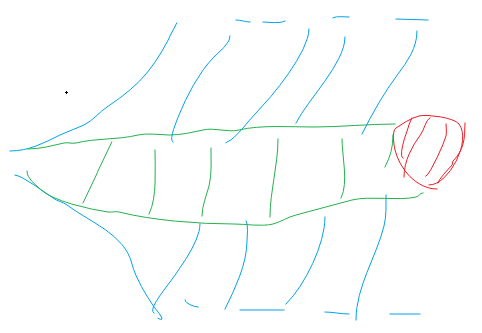
一般来说， A-STAR 适用的题目估计函数都比较成熟，拿来直接套用即可，能用的题目也不多。如果需要自己构造猜测，只要满足核心条件即可。

也就是说，在满足绿色空间小于等于蓝色空间的前提下，绿色空间越小说明启发函数写的越好。（剔除掉尽可能多的无用状态）

八数码问题

有一个奇奇怪怪的结论。

将矩阵转化为正常遍历得到的一个线性序列。如果该序列逆序对个数为偶数，则有解；如果逆序对个数为奇数，则无解。根据这个就能特判剔除无解的情况，满足 A-STAR 算法的前提条件。

估价函数：当前状态中每个数与他目标位置的曼哈顿距离之和

因为每一步只会动一个，如果动的是正确方向，那么估值函数得到的值和实际距离相等；如果动的是错误方向，那么估值函数得到的值小于实际距离，满足估值函数的合法条件。

一个有趣的小应用：如果某个值在序列的位置是 $p os$ （从0开始算起），那么他的坐标为 $(pos/3,pos $ $m o d$ $3)$ 。根据这个找到 $x$ 在序列中的位置就可以上下左右交换字符来扩展状态了。

声明一个哈希表，存储的是某个状态到起始状态的步数。

因为要输出操作序列，所以还要声明一个哈希表用于记录前驱状态和操作符。

需要特别注意push进队列的 $f i rs t$ 是 $d i s [n o w] + g e t (n o w)$ ，不要习惯性写成最短路的写法。

遍历时碰到终点出队时就break掉输出答案。

其他细节以及具体实现看代码

unordered_map<string, int> dis;                //当前状态与起点的步数
unordered_map<string, pair<string, char>> pre; //前驱，用于输出答案用
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};
char op[4] = {'r', 'l', 'u', 'd'};
typedef pair<int, string> pis;

int get(string s) {
    //估值函数，当前状态中每个数与他目标位置的曼哈顿距离之和
    int ans = 0;
    for (int i = 0; i < 9; i++) {
        if (s[i] == 'x')
            continue;
        int x = s[i] - '1';
        ans += abs(x / 3 - i / 3) + abs(x % 3 - i % 3);
    }
    return ans;
}

string bfs(string start) {
    priority_queue<pis, vector<pis>, greater<pis>> q;
    dis[start] = 0;
    q.push({get(start), start});
    while (q.size()) {
        string now = q.top().second; //当前的状态
        int step = dis[now];         //当前状态距离起点的步数
        q.pop();
        if (now == "12345678x")
            break;
        int pos = now.find('x');
        int x = pos / 3, y = pos % 3; //记录'x'的坐标位置
        string data = now;            //保存原始数据，等会会变，并且记录答案时要用到前驱
        for (int i = 0; i < 4; i++) {
            int xx = x + dx[i], yy = y + dy[i];
            if (xx >= 3 || xx < 0 || yy >= 3 || yy < 0)
                continue;
            swap(now[x * 3 + y], now[xx * 3 + yy]);     //枚举并交换'x'的位置，尝试扩展状态
            if (!dis.count(now) || dis[now] > step + 1) {
                //如果还未更新过或者可以继续更新
                dis[now] = step + 1;
                pre[now] = {data, op[i]};
                q.push({dis[now] + get(now), now});
            }
            now = data; //恢复现场
        }
    }
    string end = "12345678x";
    string ans = "";
    while (start != end) {
        ans += pre[end].second;
        end = pre[end].first;
    }
    reverse(ans.begin(), ans.end());
    return ans;
}

void solve() {
    string start, tmp;
    for (int i = 0; i < 9; i++) {
        char c;
        cin >> c;
        start += c;
        if (c != 'x')
            tmp += c;
    }
    int cnt = 0; //逆序对数量
    for (int i = 0; i < 8; i++)
        for (int j = i + 1; j < 8; j++)
            if (tmp[i] > tmp[j])
                cnt++;
    if (cnt & 1)
        cout << "unsolvable" << endl;
    else
        cout << bfs(start) << endl;
}

K短路问题

这题的估值函数就比较好想，为当前点到终点的最短距离。

结论：优先队列弹出 $k$ 次后，此时的 $d i s$ 为 $k$ 小值

所以只需反着跑一遍最短路，求出每个点到终点的最小值。再正着跑一遍 A-STAR ，记录弹出顶点为 end 的次数。当次数等于 $k$ 时，就把现在的 $d i s t an ce$ 输出。遍历时不用考虑是否已经更新过(A-STAR 算法不用判重)，是否满足松弛条件（除了终点，A-STAR 算法无法保证最优解），一股脑往优先队列里塞扩展状态。

int n, m;
int s, e, k;
int vis[MAXN], dis[MAXN];
int cnt[MAXN]; //剪枝玄学优化，能加速
int head[MAXN];
int rhead[MAXN];
int tot;
struct EDGE {
    int to, next, val;
} edge[MAXM];
void add_edge(int h[], int from, int to, int val) {
    edge[++tot].to = to;
    edge[tot].val = val;
    edge[tot].next = h[from];
    h[from] = tot;
}

void dij(int s) {
    memset(dis, 0x3f, sizeof dis);
    dis[s] = 0;
    priority_queue<pii, vector<pii>, greater<pii>> q;
    q.push({0, s});
    while (q.size()) {
        int now = q.top().second;
        int distance = q.top().first;
        q.pop();
        if (vis[now])
            continue;
        vis[now] = 1;
        for (int i = rhead[now]; i; i = edge[i].next) {
            //有向边，反着遍历求最短路
            int to = edge[i].to;
            int val = edge[i].val;
            if (dis[to] > distance + val) {
                dis[to] = distance + val;
                q.push({dis[to], to});
            }
        }
    }
}

int astar(int s, int e, int k) {
    priority_queue<piii, vector<piii>, greater<piii>> q;
    q.push({dis[s], {0, s}});
    while (q.size()) {
        int distance = q.top().second.first;
        int now = q.top().second.second;
        q.pop();
        cnt[now]++;
        if (cnt[e] == k)
            return distance; //此时的值为k短路
        for (int i = head[now]; i; i = edge[i].next) {
            int to = edge[i].to;
            int val = edge[i].val;
            if (cnt[to] < k) //剪枝玄学优化
                q.push({dis[to] + distance + val, {distance + val, to}});
        }
    }
    return -1; //没有k短路
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        add_edge(head, u, v, w), add_edge(rhead, v, u, w);
    }
    cin >> s >> e >> k;
    if (s == e)
        k++;

    dij(e);
    cout << astar(s, e, k) << endl;
}

DFS

连通性问题

不同于 $BFS$ ，基于 $D FS$ 的问题只能判断连通性，不能求最小距离。

唯一好处，代码少写点。

题目： 给出一个只包含两种颜色瓷砖的房间，每次只能在同种颜色的瓷砖上移动。给出起始位置，问可移动的范围。

int n, m;
int vis[MAXN][MAXN];
char mp[MAXN][MAXN];
int cnt = 0;
int sx, sy;
int dx[4] = {0, 0, -1, 1};
int dy[4] = {1, -1, 0, 0};

void dfs(int x, int y) {
    vis[x][y] = 1;
    for (int i = 0; i < 4; i++) {
        int xx = x + dx[i], yy = y + dy[i];
        if (xx < 1 || x > n || yy < 1 || yy > m)
            continue;
        if (vis[xx][yy])
            continue;
        if (mp[xx][yy] == '#')
            continue;
        dfs(xx, yy);
    }
}

void init() {
    cnt = 0;
    memset(vis, 0, sizeof(vis));
}

void solve() {
    init();
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            cin >> mp[i][j];
            if (mp[i][j] == '@')
                sx = i, sy = j;
        }
    dfs(sx, sy);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cnt += vis[i][j];
    cout << cnt << endl;
}

int main() {
    while (cin >> m >> n) {
        if (!n && !m)
            break;
        solve();
    }
    return 0;
}

回溯问题和搜索顺序

之前一直搞不懂这个东西。现在感觉是这样的：

如果是在图的内部搜索，例如判断连通性问题就不用回溯。

如果是将整张图看成一个状态（外部搜索），根据这个状态来进行更深一层的搜索，因为是深度优先，当前状态不会影响下一个同一层的状态，每次搜索完之后就要恢复现场。

先递归再改变不用恢复现场，先改变再递归要恢复现场。

如何做到不重不漏的搜索出所有状态？

深度优先搜索根据搜索状态出来的是一个树形结构。

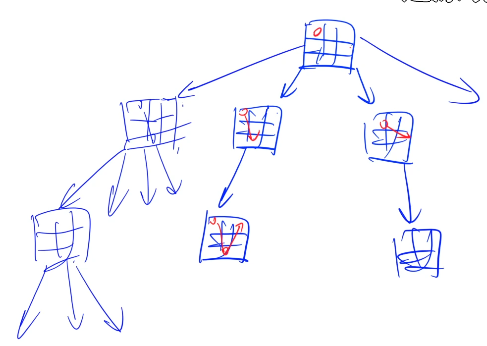
如果在某个节点找到了答案那么直接返回结果。

如果某个节点的子状态还没遍历完就继续搜索他的子状态。

如果所有子状态都搜索完成后就需要保存当前的状态（恢复现场），然后回溯到父亲节点的状态继续搜索父亲节点的子状态

题目： 给出象棋马的初始位置和棋盘的大小 $\times m$ ，问马有多少种途径遍历棋盘上的所有点

int n, m, a, b, ans;
int vis[20][20];
int dx[8] = {2, 1, -1, -2, -2, -1, 1, 2}; 
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1}; 
void dfs(int x, int y, int step) {
    if (step == n * m) {          
        ans++; 
        return;
    }
    for (int i = 0; i < 8; i++) {
        int xx = x + dx[i];
        int yy = y + dy[i];
        if (xx >= 0 && xx < n && yy >= 0 && yy < m && vis[xx][yy] == 0) {                    
            vis[xx][yy] = 1; //标记
            dfs(xx, yy, step + 1);
            vis[xx][yy] = 0; //回溯
        }
    }
}

void solve() {
    ans = 0;
    memset(vis, 0, sizeof vis);
    cin >> n >> m >> a >> b;
    vis[a][b] = 1; //标记起点
    dfs(a, b, 1);
    cout << ans << endl;
}

题目： 已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”，每个单词最多被使用两次。在两个单词相连时，其重合部分合为一部分，例如 beast 和 astonish ，如果接成一条龙则变为 beastonish。输出这条龙的最大长度

我们可以任意选择重合部分的长度，但其长度必须大于等于1，且严格小于两个串的长度，例如 at 和 atide 间不能相连。

string dic[MAXN];
int mp[MAXN][MAXN]; //i单词的结尾和j单词的开头重合部分的长度
int vis[MAXN]; //计数
int n;
int ans;
char start;

void dfs(int dragon, int last) {
    ans = max(ans, dragon);
    for (int i = 1; i <= n; i++) {
        if (mp[last][i] && vis[i] < 2) {
            vis[i]++;
            dfs(dragon + dic[i].size() - mp[last][i], i);
            vis[i]--;
        }
    }
}

void solve() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> dic[i];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            for (int k = 1; k <= min(dic[i].size(), dic[j].size()); k++) {
                string a = dic[i], b = dic[j];
                if (a.substr(a.size() - k, k) == b.substr(0, k)) {
                    mp[i][j] = k; //类似于图论中的连边
                    break;
                }
            }
        }
    }
    cin >> start;
    for (int i = 1; i <= n; i++) {
        if (dic[i][0] == start) {
            vis[i]++;
            dfs(dic[i].size(), i);
        }
        memset(vis, 0, sizeof vis);
    }
    cout << ans << endl;
}

题目： 给定 $n$ 个整数，将它们分组，使得每组中任意两个数互质。至少要分成多少个组。

int n;
int a[MAXN];
int mp[MAXN][MAXN]; //存放每个组内存放的数的序号
int ans = MAXN;
int vis[MAXN]; //看看某个数有没有被放进组内
ll gcd(ll a, ll b) {
    if (a < b)
        swap(a, b);
    ll tmp;
    while (b) {
        tmp = b;
        b = a % b;
        a = tmp;
    }
    return a;
}

bool check(int mp[], int s, int start) {
    for (int j = 0; j < start; j++) {
        if (gcd(a[mp[j]], s) > 1)
            return false;
    }
    return true;
}

void dfs(int now, int g_cur, int t_cur, int start) {
    //now为组数
    //g_cur为当前组内搜索到的数的序号
    //t_cur为搜索过的数字
    //start为当前组开始搜索的数的序号
    if (now >= ans) //最优性剪枝
        return;     
    if (t_cur == n) {
        ans = min(ans, now);
    }
    bool flag = true;
    for (int i = start; i < n; i++) {
        if (!vis[i] && check(mp[now], a[i], g_cur)) {
            //如果与组内元素都互质
            vis[i] = 1;
            mp[now][g_cur] = i;
            dfs(now, g_cur + 1, t_cur + 1, i + 1);
            vis[i] = 0;
            flag = false;
        }
    }
    if (flag) //当前组内找不到，找下一个组
        dfs(now + 1, 0, t_cur, 0);
}

void solve() {
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> a[i];
    dfs(1, 0, 0, 0);
    cout << ans << endl;
}

剪枝

常用策略

优化搜索顺序，一般情况下，优先搜索分支较少的节点
排除等效冗余，不搜索重复状态
可行性剪枝，遇到非法情况提前退出
最优性剪枝，计算最值时大于等于当前的最优解提前退出
记忆化搜索（ $D P$ ）

题目： 索道上的缆车最大承重量为 $W$ ，而 $N$ 只小猫的重量已给出，每辆缆车上的小猫重量之和不超过 $W$ 。问最少要租多少缆车。

优化搜索顺序，先搜索重量大的猫。

int n, mx;
int a[MAXN];
int rem[MAXN]; //某辆车剩余的空间
int ans = MAXN;

void dfs(int now, int k) {
    //当前的猫，当前拥有的车的数量
    if (k >= ans) //最优性剪枝
        return;
    if (now == n + 1) {
        ans = k;
        return;
    }
    //两种状态，塞进一辆缆车或者新租一辆缆车
    for (int i = 1; i <= k; i++) {
        if (a[now] <= rem[i]) {
            rem[i] -= a[now];
            dfs(now + 1, k);
            rem[i] += a[now];
        }
    }
    rem[k + 1] -= a[now];
    dfs(now + 1, k + 1);
    rem[k + 1] += a[now];
}

void solve() {
    cin >> n >> mx;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    sort(a + 1, a + 1 + n, greater<>());
    for (int i = 1; i <= n; i++)
        rem[i] = mx;
    dfs(1, 1);
    cout << ans << endl;
}

题目： 乔治拿来一组等长的木棒，将它们随机地斩断，使得每一节木棍的长度都不超过 $50$ 个长度单位。然后他又想把这些木棍恢复到为之前的状态，但忘记了初始时有多少木棒以及木棒的初始长度。帮助乔治计算木棒的可能最小长度。

四个优化：

枚举的长度必须为总长度的约数
如果第 $i$ 根大棍失败了，那么长度与 $i$ 相同的大棍也会失败
小棍从大到小枚举，优化搜索顺序
如果第一次尝试拼入木棍就失败的话，那么这个策略必然是失败的。

int n;
int sum;
int a[MAXN]; //小棍长度
int vis[MAXN];
int length;

bool dfs(int now, int len, int start) {
    //正在枚举第now根大棍，长度为len，从第start根小棍开始找
    if ((now - 1) * length == sum)
        return true;
    if (len == length)
        return dfs(now + 1, 0, 0);
    for (int i = start + 1; i <= n; i++) {
        if (vis[i])
            continue;
        if (len + a[i] > length)
            continue; //可行性剪枝
        vis[i] = 1;
        if (len + a[i] <= length)
            if (dfs(now, len + a[i], i))
                return true;
        vis[i] = 0; //恢复现场
        //走到这说明第i根木棍失败了
        if (!len)
            return false;
        if (len + a[i] == length)
            return false;
        int j = i;
        while (j <= n && a[j] == a[i])
            j++;
        i = j - 1;
    }
    //所有木棒试了遍依然不行
    return false;
}

void solve() {
    memset(vis, 0, sizeof vis);
    sum = 0;
    int mx = 0;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        sum += a[i];
        mx = max(mx, a[i]);
    }
    sort(a + 1, a + 1 + n, greater<>());
    for (int i = mx; i <= sum; i++) {
        //大棍长度一定要大于等于所有小棍的最大值
        if (sum % i)
            continue;
        length = i;
        if (dfs(1, 0, 0)) {
            cout << i << endl;
            return;
        }
    }
}

迭代加深

当搜索树深度比较深的情况下，一层一层搜索（限定深度）防止如下的情况发生。思想类似于BFS

题目： 使用上取整，下取整，阶乘，算术平方根四种运算，完成对一个数字的变换。每次阶乘记为一步，每次开根号并向上/向下取整记为一步。找到从 $x$ 到 $y$ 变换的最小步数。

ll a, b;
bool flag;
int path[MAXN];
ll get(ll x) {
    ll ans = 1;
    for (ll i = 2; i <= x; i++)
        ans *= i;
    return ans;
}
bool dfs(ll num, int now, int depth) {
    if (num == b) {
        printf("%lld\n", now);
        flag = true;
        return true;
    }
    if (now == depth)
        return false; //迭代加深
    if (dfs(get(num), now + 1, depth))
        return true;
    ll tmp = sqrt(num);
    if (dfs(tmp, now + 1, depth))
        return true;
    if (tmp * tmp != num) {
        if (dfs(tmp + 1, now + 1, depth))
            return true;
    }
    return false;
}

void solve() {
    a = read(), b = read();
    int depth = 1;
    if (a == b) {
        puts("0");
        return;
    }
    flag = false;
    while (depth <= 7 && !dfs(a, 0, depth)) {
        depth++;
    }
    if (!flag)
        puts("-1");
}

题目： 满足如下条件的长度为 $m$ 的序列 $X$ 被称为加成序列：

$X [1] = 1$
$X [m] = n$
严格递增
对于每个 $\leq k \leq m)$ ，都存在两个整数 $i$ 和 $\leq i, j \leq k - 1)$ ， $i$ 和 $j$ 可相等，使得 $X [k] = X [i] + X [j]$ 。

找出符合上述条件的长度 $m$ 最小的加成序列。

int n;
int vis[MAXN], path[MAXN];
bool dfs(int now, int mx) {
    //当前深度与最大深度
    if (now > mx)
        return false; //可行性剪枝
    if (path[now - 1] == n && now == mx)
        return true;
    memset(vis, 0, sizeof vis);
    vis[1] = 1;
    for (int i = now - 1; i; i--) {
        for (int j = i; j; j--) {
            int sum = path[i] + path[j];
            if (vis[sum])
                continue; //可行性剪枝
            if (sum <= path[now - 1])
                continue; //可行性剪枝，严格递增序列
            if (sum > n)
                continue; //可行性剪枝，严格递增序列
            vis[sum] = 1;
            path[now] = sum;
            if (dfs(now + 1, mx))
                return true;
            path[now] = 0;
        }
    }
    return false;
}

void solve() {
    int depth = 2;
    path[1] = 1; //哨兵
    while (!dfs(2, depth))
        depth++; //迭代加深
    for (int i = 1; i < depth; i++)
        cout << path[i] << " ";
    cout << endl;
}

int main() {
    while (cin >> n && n)
        solve();
    return 0;
}

原文链接：https://blog.csdn.net/m0_51145827/article/details/126161555