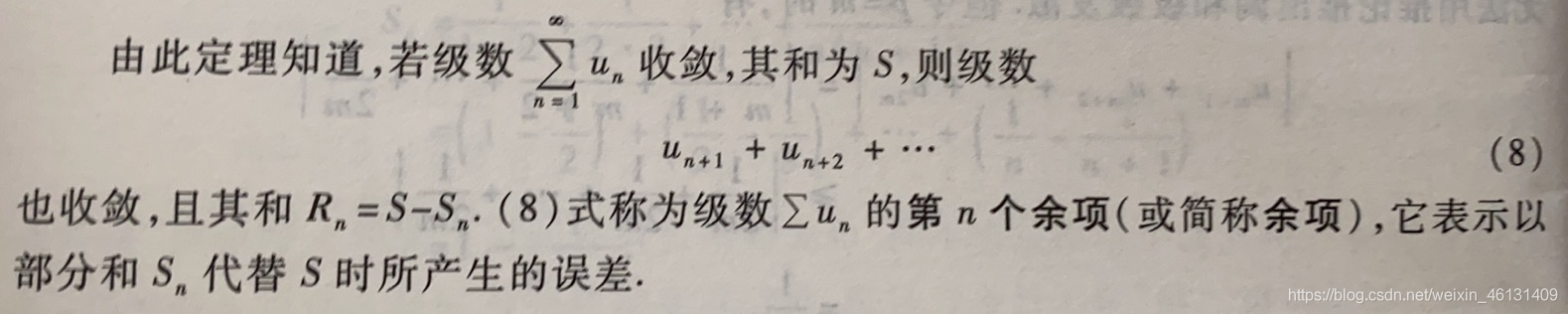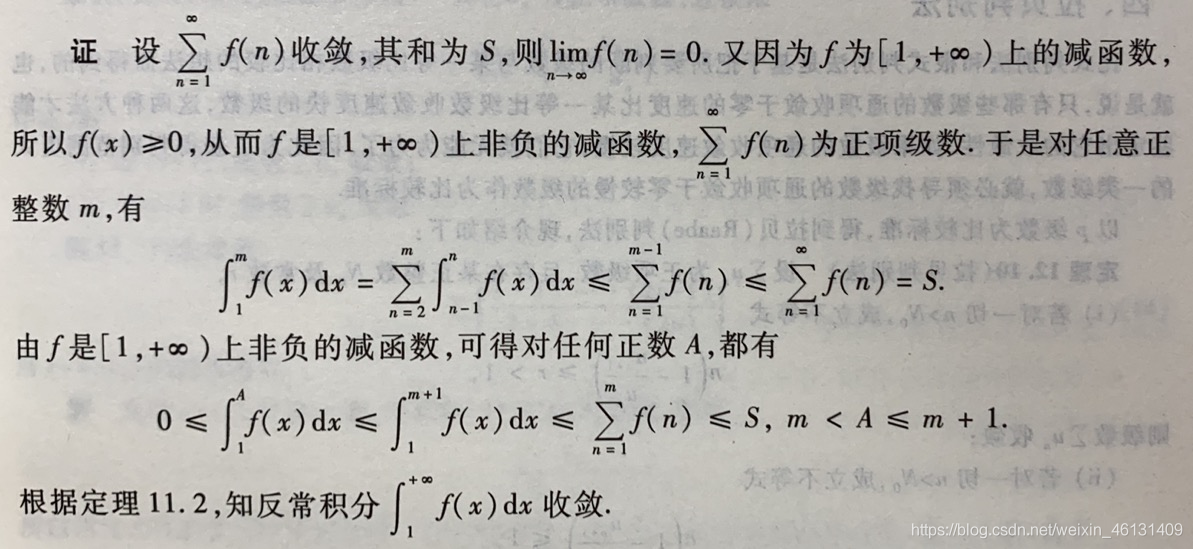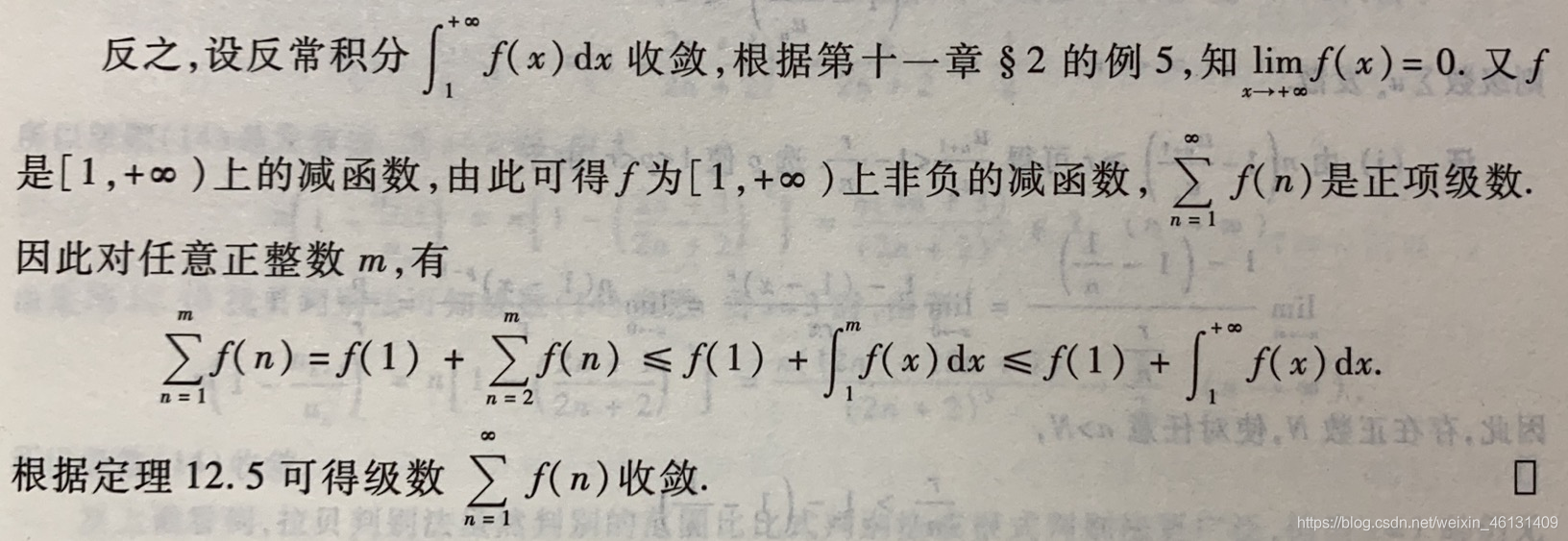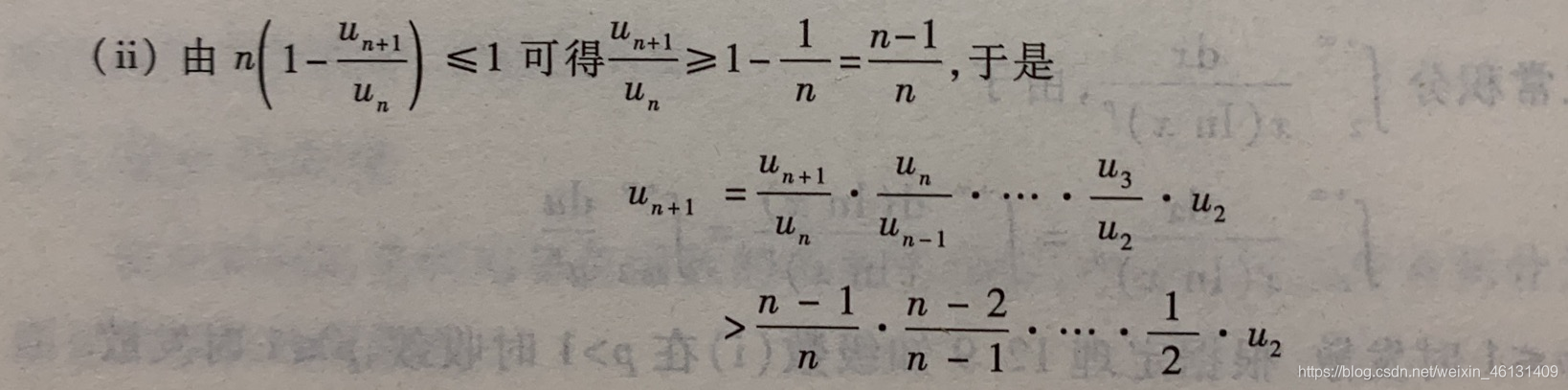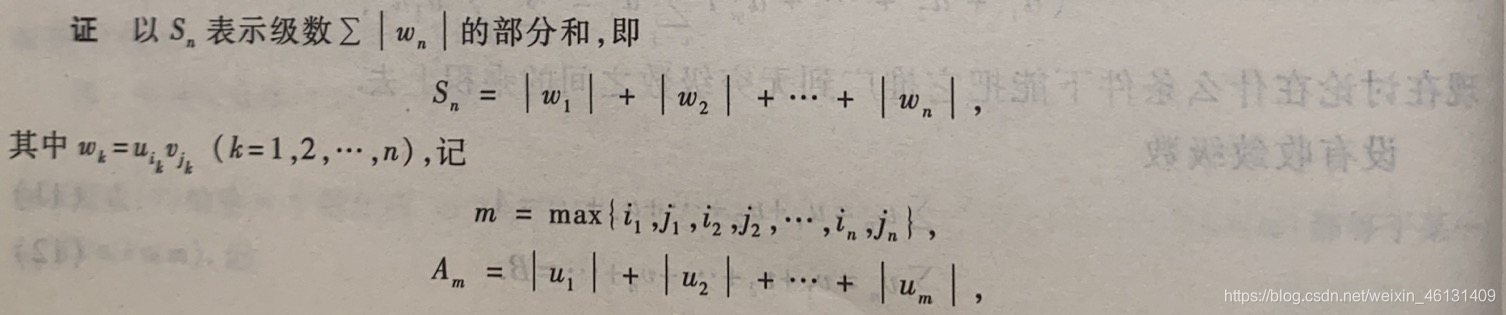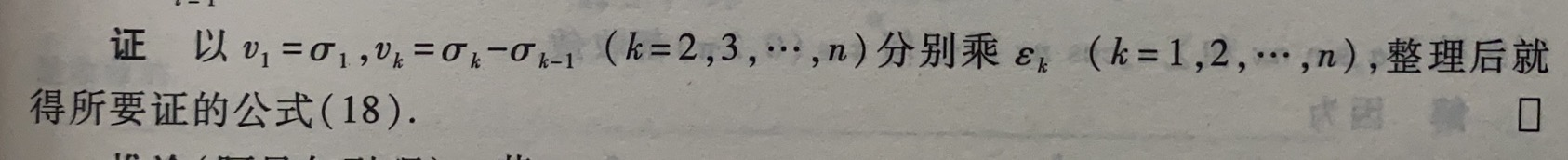一.级数的敛散性
1.相关概念
(1)数项级数与部分和数列:
(2)收敛与发散:

(3)原级数与部分和数列的关系:
2.级数收敛的柯西准则:
定理12.1:级数(1)收敛的充要条件是:对∀ ε > 0 , ∃ N ∈ N + ∀ε>0,∃N∈N_+∀ε>0,∃N∈N+,使得当m > N m>Nm>N时,对∀ p ∈ N + ∀p∈N_+∀p∈N+都有∣ u m + 1 + . . . + u m + p ∣ < ε ( 6 ) |u_{m+1}+...+u_{m+p}|<ε\qquad(6)∣um+1+...+um+p∣<ε(6)
相应地,级数(1)发散的充要条件是:∃ ε 0 > 0 ∃ε_0>0∃ε0>0,对∀ N ∈ N + ∀N∈N_+∀N∈N+,总∃ N < m 0 ∈ N + ∃N<m_0∈N_+∃N<m0∈N+和p 0 ∈ N + p_0∈N_+p0∈N+,有∣ u m 0 + 1 + . . . + u m 0 + p 0 ∣ ≥ ε 0 ( 7 ) |u_{m_0+1}+...+u_{m_0+p_0}|≥ε_0\qquad(7)∣um0+1+...+um0+p0∣≥ε0(7)
推论:若级数(1)收敛,则lim n → ∞ u n = 0 \displaystyle\lim_{n \to \infty}u_n=0n→∞limun=0
3.级数的性质:
定理12.2:若级数∑ u n , ∑ v n \sum u_n,\sum v_n∑un,∑vn均收敛,则对∀常数c , d c,dc,d,级数∑ ( c u n + d v n ) \sum(cu_n+dv_n)∑(cun+dvn)也收敛,且∑ ( c u n + d v n ) = c ∑ u n + d ∑ v n \sum(cu_n+dv_n)=c\sum u_n+d\sum v_n∑(cun+dvn)=c∑un+d∑vn
定理12.3:去除/增加/改变级数的有限个项不改变级数的敛散性
定理12.4:在收敛级数的项中任意加括号,既不改变级数的收敛性,也不改变级数的和
注意:该性质仅适用于收敛级数,对发散级数不适用;因此,从级数加括号后的收敛,不能推断其在加括号前也收敛,如( 1 − 1 ) + ( 1 − 1 ) + . . . + ( 1 − 1 ) + . . . = 0 + 0 + . . . + 0 + . . . = 0 (1-1)+(1-1)+...+(1-1)+...=0+0+...+0+...=0(1−1)+(1−1)+...+(1−1)+...=0+0+...+0+...=0收敛,但1 − 1 + 1 − 1 + . . . + 1 − 1 + . . . 1-1+1-1+...+1-1+...1−1+1−1+...+1−1+...却是发散的
二.正项级数
1.一般判别原则
(1)正项级数收敛的充要条件:
定理12.5:正项级数∑ u n \sum u_n∑un收敛的充要条件是:部分和数列{ S n } \{S_n\}{Sn}有界,即∃ M > 0 ∃M>0∃M>0,对∀ n ∈ N + ∀n∈N_+∀n∈N+有S n < M S_n<MSn<M
(2)正项级数收敛的比较判别法:
定理12.6:设∑ u n , ∑ v n \sum u_n,\sum v_n∑un,∑vn是2个正项级数,如果∃ N > 0 ∃N>0∃N>0,对∀ n > N ∀n>N∀n>N都有u n ≤ v n ( 1 ) u_n≤v_n\qquad(1)un≤vn(1)则:①若∑ v n \sum v_n∑vn收敛,则∑ u n \sum u_n∑un也收敛
\:\:\:\:\:②若∑ u n \sum u_n∑un发散,则∑ v n \sum v_n∑vn也发散
2.比值判别法与根值判别法
(1)达朗贝尔判别法(D’Alembert Discriminance;比值判别法):
定理12.7:设∑ u n \sum u_n∑un为正项级数,且∃ N 0 ∈ N + ∃N_0∈N_+∃N0∈N+及常数0 < q < 1 0<q<10<q<1,则
①若对∀ n > N 0 ∀n>N_0∀n>N0,有不等式u n + 1 u n ≤ q ( 7 ) \frac{u_{n+1}}{u_n}≤q\qquad(7)unun+1≤q(7)成立,则∑ u n \sum u_n∑un收敛
②若对∀ n > N 0 ∀n>N_0∀n>N0,有不等式u n + 1 u n ≥ 1 ( 8 ) \frac{u_{n+1}}{u_n}≥1\qquad(8)unun+1≥1(8)成立,则∑ u n \sum u_n∑un发散
推论1(比值判别法的极限形式):设∑ u n \sum u_n∑un为正项级数,且lim n → ∞ u n + 1 u n = q ( 9 ) \displaystyle\lim_{n \to \infty}\frac{u_{n+1}}{u_n}=q\qquad(9)n→∞limunun+1=q(9)则①当q < 1 q<1q<1,∑ u n \sum u_n∑un收敛
\:\:\:\:②当q > 1 q>1q>1或q = + ∞ q=+\inftyq=+∞,∑ u n \sum u_n∑un收敛
如果某级数的(9)式的极限不存在,则可使用上/下极限来判别
推论2:设∑ u n \sum u_n∑un为正项级数,则
①若lim n → ∞ ‾ u n + 1 u n = q < 1 \overline{\displaystyle\lim_{n \to \infty}}\frac{u_{n+1}}{u_n}=q<1n→∞limunun+1=q<1,则∑ u n \sum u_n∑un收敛
②若lim n → ∞ ‾ u n + 1 u n = q > 1 \underline{\displaystyle\lim_{n \to \infty}}\frac{u_{n+1}}{u_n}=q>1n→∞limunun+1=q>1,则∑ u n \sum u_n∑un发散
(2)柯西判别法(Cauchy Discriminance;根值判别法):
定理12.8:设∑ u n \sum u_n∑un为正项级数,且∃ N 0 > 0 ∃N_0>0∃N0>0及常数l > 0 l>0l>0,则
①若对∀ n > N 0 ∀n>N_0∀n>N0,有不等式u n n ≤ l < 1 ( 11 ) \sqrt[n]{u_n}≤l<1\qquad(11)nun≤l<1(11)成立,则∑ u n \sum u_n∑un收敛
②若对∀ n > N 0 ∀n>N_0∀n>N0,有不等式u n n ≥ 1 ( 12 ) \sqrt[n]{u_n}≥1\qquad(12)nun≥1(12)成立,则∑ u n \sum u_n∑un发散
推论1(根值判别法的极限形式):设∑ u n \sum u_n∑un为正项级数,且lim n → ∞ u n n = l ( 13 ) \displaystyle\lim_{n \to \infty}\sqrt[n]{u_n}=l\qquad(13)n→∞limnun=l(13)则①当l < 1 l<1l<1,∑ u n \sum u_n∑un收敛
\:\:\:\:②当l > 1 l>1l>1,∑ u n \sum u_n∑un收敛
如果某级数的(13)式的极限不存在,则可使用上极限来判别
推论2:设∑ u n \sum u_n∑un为正项级数,且lim n → ∞ ‾ u n n = l \overline{\displaystyle\lim_{n \to \infty}}\sqrt[n]{u_n}=ln→∞limnun=l则当①l < 1 l<1l<1,∑ u n \sum u_n∑un收敛
\quad\:\:\:②l > 1 l>1l>1,∑ u n \sum u_n∑un发散
3.积分判别法
定理12.9:设f ff为[ 1 , + ∞ ) [1,+\infty)[1,+∞)上的减函数,则级数∑ n = 1 ∞ f ( n ) \displaystyle\sum_{n=1}^\infty{f(n)}n=1∑∞f(n)收敛的充要条件是:无穷积分∫ 1 + ∞ f ( x ) d x \int_1^{+\infty}f(x)dx∫1+∞f(x)dx收敛
4.拉贝判别法(Raabe Discriminance):
以p级数为比较标准,就得到拉贝判别法
定理12.10:设∑ u n \sum u_n∑un为正项级数,且∃ N 0 ∈ N + ∃N_0∈N_+∃N0∈N+及常数r > 1 r>1r>1,则
①若对∀ n > N 0 ∀n>N_0∀n>N0,有不等式n ( 1 − u n + 1 u n ) ≥ r n(1-\frac{u_{n+1}}{u_n})≥rn(1−unun+1)≥r成立,则∑ u n \sum u_n∑un收敛
②若对∀ n > N 0 ∀n>N_0∀n>N0,有不等式n ( 1 − u n + 1 u n ) ≤ 1 n(1-\frac{u_{n+1}}{u_n})≤1n(1−unun+1)≤1成立,则∑ u n \sum u_n∑un发散
推论(拉贝判别法的极限形式):设∑ u n \sum u_n∑un为正项级数,且极限lim n → ∞ n ( 1 − u n + 1 u n ) \displaystyle\lim_{n \to \infty}n(1-\frac{u_{n+1}}{u_n})n→∞limn(1−unun+1)存在,则
①当r > 1 r>1r>1时,∑ u n \sum u_n∑un收敛
②当r < 1 r<1r<1时,∑ u n \sum u_n∑un发散
虽然拉贝判别法判别的范围比比值判别法或根值判别法更广泛,但当r = 1 r=1r=1时仍无法判别;由于没有收敛得最慢的收敛数.因此任何判别法都只能解决某类级数的收敛问题,而不能解决所有级数的收敛问题;当然,还可以建立比拉贝判别法更精细有效的判别法,但这个过程是无限的
三.一般项级数
1.交错级数
(1)概念: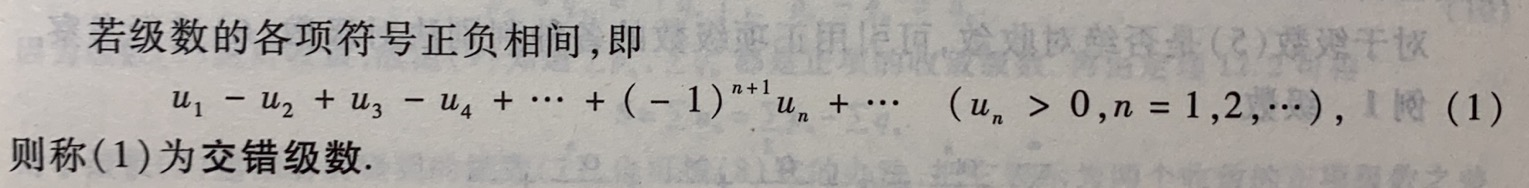
(2)莱布尼兹判别法(Leibnitz Discriminance):
定理12.11:若交错级数(1)满足:
①数列{ u n } \{u_n\}{un}单调递减
②lim n → ∞ u n = 0 \displaystyle\lim_{n \to \infty}u_n=0n→∞limun=0
则交错级数(1)收敛
推论:若交错级数(1)满足莱布尼兹判别法的条件,则其余项估计式为:∣ R n ∣ ≤ u n + 1 |R_n|≤u_{n+1}∣Rn∣≤un+1
2.绝对收敛级数
(1)概念:

关于级数(5)是否绝对收敛,可使用正项级数的判别法考察级数(6)
若级数(5)收敛,但级数(6)不收敛,则称级数(5)为条件收敛级数
(2)绝对收敛级数的敛散性:
定理12.12:绝对收敛级数一定收敛
(3)绝对收敛级数的性质:
级数的重排:
定理12.13:设级数(5)绝对收敛,且其和等于S SS,则任意重排后得到的级数(7)也绝对收敛,且有相同的和数
注意:由条件收敛级数重排后得到的新级数,即使收敛,也不一定收敛于原来的和数
实际上,条件收敛级数适当重排后,可得到发散级数或收敛于任何指定数的级数
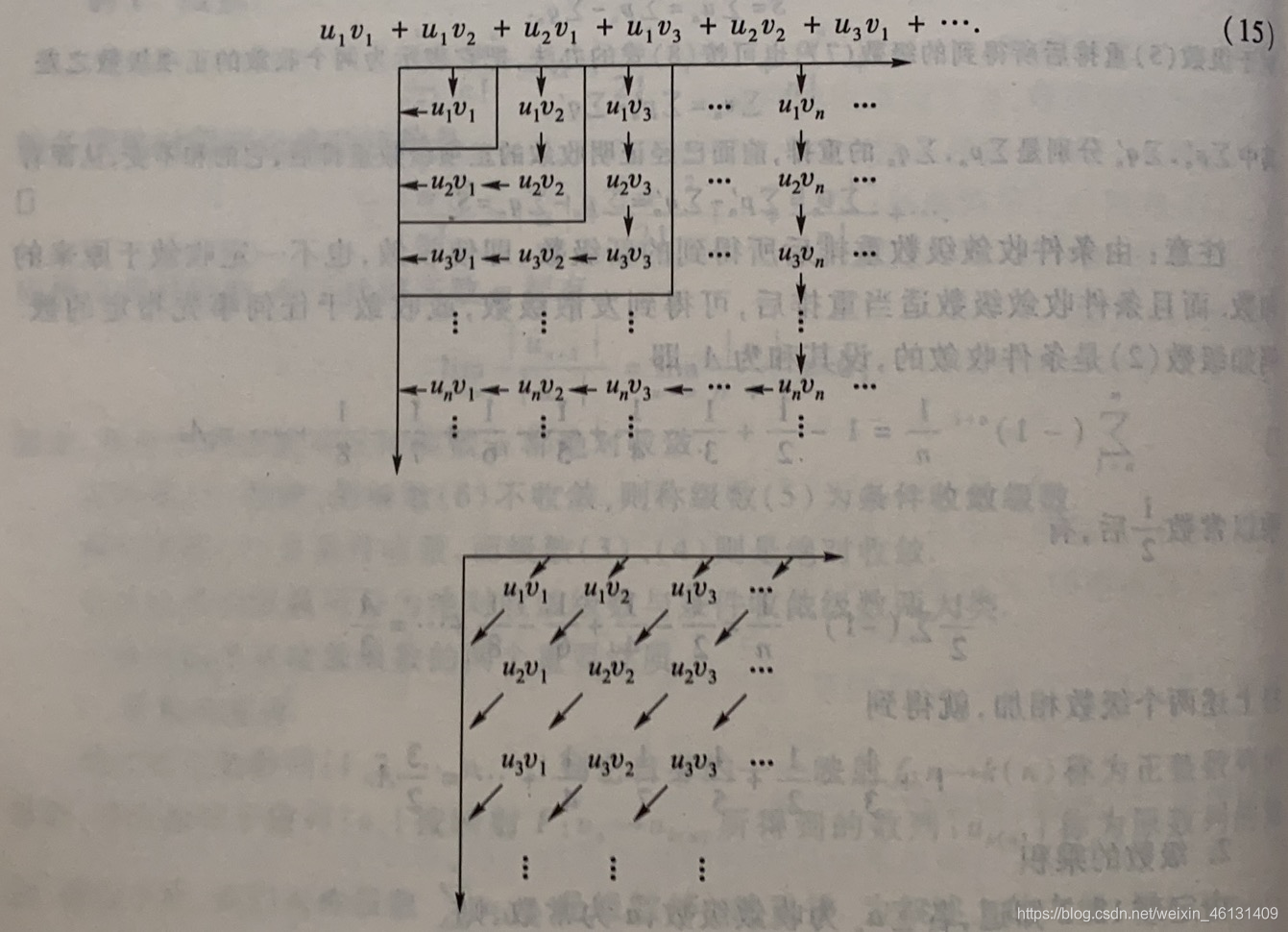
级数的乘积:
定理12.14(柯西定理):若级数(11),(12)都绝对收敛,则对(13)中所有乘积按任意顺序排列所得到的级数∑ i , j u i v j = ∑ w n \displaystyle\sum_{i,j}u_iv_j=\sum w_ni,j∑uivj=∑wn也绝对收敛,且其和等于A B ABAB
3.阿贝尔判别法与狄利克雷判别法
(1)分部求和公式(阿贝尔变换):
引理:设ε i , v i ( i = 1 , 2... n ) ε_i,v_i\,(i=1,2...n)εi,vi(i=1,2...n)为2组实数,若令σ k = v 1 + v 2 + . . . + v k ( k = 1 , 2... n ) σ_k=v_1+v_2+...+v_k\,(k=1,2...n)σk=v1+v2+...+vk(k=1,2...n)则有如下分布求和公式成立:∑ i = 1 n ε i v i = ( ε 1 − ε 2 ) σ 1 + ( ε 2 − ε 3 ) σ 2 + . . . + ( ε n − 1 − ε n ) σ n − 1 + ε n σ n ( 18 ) \displaystyle\sum_{i=1}^nε_iv_i=(ε_1-ε_2)σ_1+(ε_2-ε_3)σ_2+...+(ε_{n-1}-ε_n)σ_{n-1}+ε_nσ_n\qquad(18)i=1∑nεivi=(ε1−ε2)σ1+(ε2−ε3)σ2+...+(εn−1−εn)σn−1+εnσn(18)
(2)阿贝尔引理:
推论:若
( i ) ε 1 , ε 2 . . . ε n (i)\:ε_1,ε_2...ε_n(i)ε1,ε2...εn是单调数组
( i i ) (ii)\:(ii)对∀ k ∈ N + ( 1 ≤ k ≤ n ) ∀k∈N_+\,(1≤k≤n)∀k∈N+(1≤k≤n)有∣ σ k ∣ ≤ A ( σ k = v 1 + . . . + v k ) |σ_k|≤A\,(σ_k=v_1+...+v_k)∣σk∣≤A(σk=v1+...+vk)
则记ε = m a x { ∣ ε k ∣ } ε=max\{|ε_k|\}ε=max{∣εk∣},有∣ ∑ k = 1 n ε k v k ∣ ≤ 3 ε A |\displaystyle\sum_{k=1}^nε_kv_k|≤3εA∣k=1∑nεkvk∣≤3εA
下面寻找用于判断级数∑ a n b n = a 1 b 1 + a 2 b 2 + . . . + a n b n + . . . ( 20 ) \sum a_nb_n=a_1b_1+a_2b_2+...+a_nb_n+...\qquad(20)∑anbn=a1b1+a2b2+...+anbn+...(20)敛散性的判别法
(3)阿贝尔判别法(Abel Discriminance):
定理12.15:若{ a n } \{a_n\}{an}为单调有界数列,且级数∑ b n \sum b_n∑bn收敛,则级数(20)收敛
由阿贝尔判别法可知:若∑ u n \sum u_n∑un收敛,则∑ u n n p ( p > 0 ) , ∑ u n n + 1 \sum\frac{u_n}{n^p}\,(p>0),\sum\frac{u_n}{\sqrt{n+1}}∑npun(p>0),∑n+1un也收敛
(4)狄利克雷判别法(Dirichlet Discriminance):
定理12.16:若数列{ a n } \{a_n\}{an}单调递减,且lim n → ∞ a n = 0 \displaystyle\lim_{n \to \infty}a_n=0n→∞liman=0,右级数∑ b n \sum b_n∑bn的部分和数列有界,则级数(20)收敛
四.一些重要级数的敛散性
1.等比级数(也称几何级数)的敛散性:
2.调和级数的敛散性:
3.p级数的敛散性: