typedef struct node{
    int data;
    node *left;
    node *right;
}Node,*Tree;

一、二叉树的层次构造

Node *generateTree(int a[],int i,int len){
    Node *node = (Node *)malloc(sizeof(Node));
    node->data = a[i];
    node->left = nullptr;
    node->right = nullptr;
    if(2*i+1<len) {
        node->left = generateTree(a, 2 * i+1, len);
    }
    if(2*i+2<len) {
        node->right = generateTree(a, 2 * i + 2, len);
    }
    return node;
}

二、二叉树的层次遍历

（1）借助队列实现层次遍历

队列的基本操作

typedef struct{
    Node data[100];
    int head,rear;
    int len;
}Queue;

bool isEmpty(Queue q){
    if(q.len == 0 ){
        return true;
    }
    else{return false;};
}

void enQueue(Queue &q,Node node){
    q.data[q.rear++] = node;
    q.len++;
}
Node outQueue(Queue &q){

    if(!isEmpty(q)) {
        printf("%d",q.data[q.head]);
        q.len--;
        return q.data[q.head++];
    }
    else{
        Node n;
        n.data=0;
        return  n;
    }
}

层次遍历

思想：将根节点入队，此后每出队一个元素，将该结点的左右孩子依次入队。直到队空。

void storeyOrder(Node *node,Queue q){
    if(node != NULL) {
        enQueue(q,*node);
    }
    while(q.len != 0) {
        Node p = outQueue(q);
        if(p.left != nullptr){
            enQueue(q,*p.left);
        }
        if(p.right != nullptr){
            enQueue(q,*p.right);
        }
    }
}

void Order_1(Queue &q,int a[],int i){
    Node* node = generateTree(a,0,i);   //根据数组a进行层次构造
    storeyOrder(node,q);                //层次遍历，正确结果的打印结果与a相同
}

（2）借助辅助数组的递归实现遍历

思想：每遍历一个结点，若父父节点下标为i,则左右结点存入2i+1,2i+2的原则，将结点存入对应的数组下标。

//计算二叉树的深度，规定最顶层深度为0
int countStorey(Tree tree,int count){     //count记录层数
    int i=count,j=count;     //i,j左右子树深度与当前结点深度相同
    if(tree->left != nullptr){
        i = countStorey(tree->left,count+1);   //i左子树深度
    }
    if(tree->right != nullptr){
        j = countStorey(tree->right,count+1);  //i左子树深度
    }
    if(i>count || j>count){          //返回三者值最大的作为已遍历子树的深度
        if(i>j){
            return i;
        }
        else{return j;};
    }
    else{
        return count;
    }
}
//完成2的n次方运算
int pow(int n){
    int i = 1;
    int x = 1;
    while(i <= n ){
        x*=2;
        i++;
    }
    return x;
}
//后续遍历，从下到上把结点数值取出，修改数组的内容。
int * storeyOrder_2(int m[],Tree tree,int i){      //i表示结点在数组m对应位置
    if(tree->left!= nullptr){
        m =storeyOrder_2(m,tree->left,2*i+1);
    }
    if(tree->right!= nullptr){
        m = storeyOrder_2(m,tree->right,2*i+2);
    }
    m[i] = tree->data;
    return m;
}

int* Order_2(Tree tree){
    int storey = countStorey(tree,0);      //计算深度
    int len = pow(storey+1)-1;        //深度为n的满二叉树的节点数2^n-1
   int m[len];                             //创建对应长度的数组
    for(int i = 0;i<len;i++){            //大小初始化为-1
        m[i]= -1;
    }
    return  storeyOrder_2(m,tree,0);      //后序遍历，从下往上，每个结点修改数组对应下标的值。返回数组头指针
}

int main() {
    Node * node1 = (Node *) malloc(sizeof(Node));
    Node * node2 = (Node *) malloc(sizeof(Node));
    Node * node3 = (Node *) malloc(sizeof(Node));
    Node * node4 = (Node *) malloc(sizeof(Node));
    node1->data=1;
    node2->data=2;
    node3->data=3;
    node4->data=4;
    node1->left=node2;
    node2->right = node3;
    node2->left =node4;
    node1->right = nullptr;
    node3->left= nullptr;
    node3->right= nullptr;
    node4->left= nullptr;
    node4->right= nullptr;

    int *x = Order_2(node1);
   
    printf("%d",*(x));
    printf("%d",*(x+1));
    printf("%d",*(x+2));
    printf("%d",*(x+3));
    printf("%d",*(x+4));
}

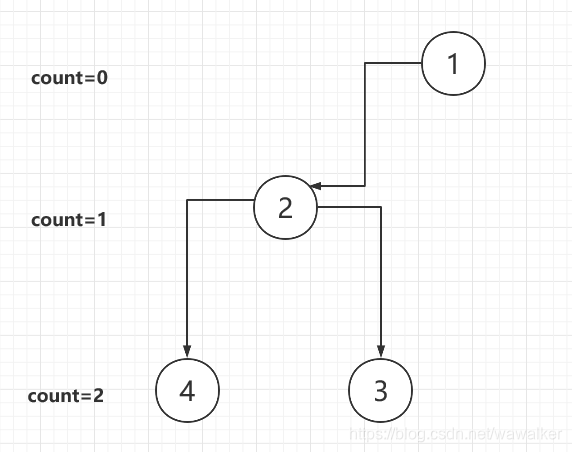
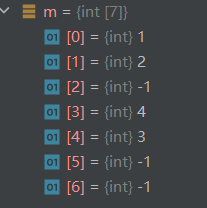
遍历数组将不等于-1的数值输出，就是层次遍历序列：1，2，4，3

奇怪的地方：输出m[0]时，会篡改a[1]的值。结果是1，6422180，-1，4，3

 数组m成功返回的是 1，2，-1，4，3，-1，-1

 但输出*m头元素时，不仅m[0]变化了，甚至还改变了m[1]。

 这就是导致m[1[错误输出的原因。在此小白我也不知道为什么产生这种情况。