1. 逻辑回归

逻辑回归是一种预测分析，解释因变量与一个或者多个自变量之间的关系，与线性回归不同之处在于它的目标变量有几种类别，所以逻辑回归主要用于解决回归问题。逻辑回归实际上是一个概率分类模型，产生0和1之间的p值。

2.实验数据

使用iris内置的数据集，不需要做预处理。

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
%matplotlib inline

#加载数据
iris = load_iris()
iris_x = iris.data
iris_y = iris.target
#stratify=iris_y是保持测试集与整个数据集里iris_y的数据分类比例一致
train_x, test_x, train_y, test_y = train_test_split(iris_x, iris_y, test_size=0.25, random_state=0, stratify=iris_y)

3.拟合预测

属性：

• coef_：权重向量
• intercept：b值
• n_iter：实际迭代次数

方法：

• fit(X, y[,sample_weight])训练模型
• predict(X)：用模型进行预测，返回预测值
• predict_proba(X)：返回一个数组，数组元素依次是X预测为各个类别的概率
• score(X, y[,sample_weight])：返回预测性能得分。score越大，预测性能越好。

• regr = LogisticRegression(max_iter = 200)
  #利用regr训练
  regr.fit(train_x, train_y)
  #回归评价
  print('Coefficients:%s, intercept %s' % (regr.coef_, regr.intercept_))
  print(''Residual sum of squares: %.2f''% np.mean((regr.predict(test_x) - test_y) ** 2))
  print('Score: %.2f' % regr.score(test_x, test_y))

  4.调参

  首先我们考察multi_class参数对分类结果的影响。默认采用的是one-ve-test策略，但是逻辑回归模型原生就支持多分类，即multi_class='multinomial'。

  注意：只有solver参数为'newton-cg'或者'lbfgs'才能配合multi_class='multinomial'，否则报错。

• regr1 = LogisticRegression(multi_class='multinomial', solver='lbfgs', max_iter = 2000)
  regr1.fit(train_x, train_y)
  print('Coefficients:%s, intercept %s' % (regr1.coef_, regr1.intercept_))
  print(''Residual sum of squares: %.2f''% np.mean((regr1.predict(test_x) - test_y) ** 2))
  print('Score: %.2f' % regr1.score(test_x, test_y))
  #在本案例中，多分类策略进一步提升了预测准确率

  接下来，我们考察参数C对分类模型预测性能的影响。C是正则化项系数的倒数，它越小，正则化项的权重越大。

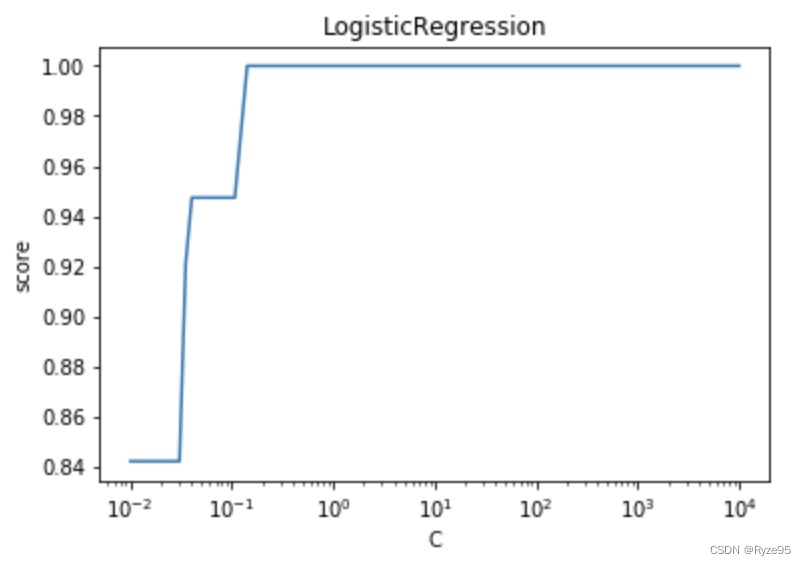
• #不显示warnings
  import warnings
  warnings.filterwarning("ignore")
  
  Cs = np.logspace(-2,4,num=100)
  score = []
  for C in Cs:
      regr2 = LogisticRegression(C=)
      regr2.fit(train_x, train_y)
      scores.append(regr2.score(test_x, test_y)
  print(scores)
  
  #scores数据太多，不利于分析，所以借助绘图分析
  fig = plt.figure()
  ax = fig.add_subplot(111)
  ax.plot(Cs, scores)
  ax.set_xlabel(r'C')
  ax.set_ylabel(r'score')
  ax.set_xscale('log')
  ax.set_title('LogisticRegression')
  plt.show()

  从图中可以看到，随着C的增大，模型的预测准确率不断上升；当C增大到一定程度，模型的预测准确率 维持在较高的水平不变。

•