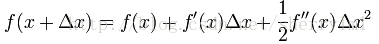概述

最优化问题的一般数学模型：
$min\ f(\mathbf x)$
$s.t. \ h_i(\mathbf x) = 0,\quad i=1,...,m;$
$\qquad g_j(\mathbf x)\ge0, \quad j=1,...,p.$

其中$\mathbf x$是n维向量，在实际问题中也被叫做决策变量，s.t.为subject to的缩写，用来表示约束条件，因此， $h_i(\mathbf x)$和$g_j(\mathbf x)$称为约束函数，其中$h_i(\mathbf x) = 0$为等式约束，$g_j(\mathbf x)\ge0$为不等式约束。求极小值的函数f称为目标函数，求极大值的问题可以通过取负数转换为极小值问题，因此这里都以极小值问题来讨论。

因此，根据有无约束函数，可以将最优化问题分为有约束最优化和无约束最优化问题;根据目标函数和约束函数的类型，可分为线性规划（目标函数和约束函数均为线性函数）和非线性规划; 另外，如目标函数为二次函数，而约束函数全部是线性函数的最优化问题称为二次规划问题，当目标函数不是数量函数而是向量函数时，就是多目标规划，还有用于姐姐多阶段决策问题的动态规划等

最优化方法的一般迭代算法，以下降算法为例：
给定初始点$\mathbf x_0, k = 0$
(1) 确定点$x_k$处的可行下降方向$\mathbf p_k$;
(2)确定步长$\alpha_k\gt 0$，使得$f(\mathbf x_k+\alpha_kp_k)\lt f(\mathbf x_k)$;
(3)令$\mathbf x_{k+1}=\mathbf x_k+\alpha_k\mathbf p_k$;
(4)若$\mathbf x_{k+1}$满足某种终止条件，则停止迭代，以$\mathbf x_{k+1}$为最优近似解，否则k=k+1，转（1）

无约束最优化问题

根据选取搜索方向时是否使用目标函数的导数，将无约束最优化问题分为两类：
1 解析法：最速下降法，Newton法，共轭梯度法，拟Newton法
2 直接法：Powell的方向加速法

梯度下降（Gradient Descent)

梯度下降法通常也称为最速下降法。最速下降法是用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢。
这里有一篇觉得写的很好：再谈 最速下降法
补充一点小结：
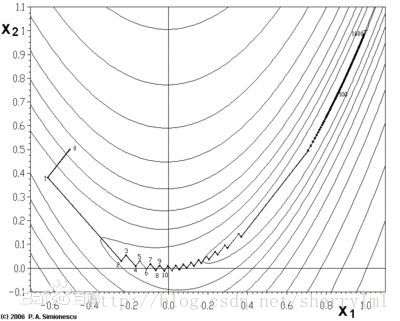
最速下降法虽然名字里有最速两个字，但其实指的是选取的下降方向针对当前局部来说是最快的下降方向，即负梯度方向，对整体来说不一定是最速下降方向。最速下降法逼近极小点的路线是锯齿形的，并且越靠近极小点步长越小，即越走越慢。

最速下降法对一般函数而言都有很好的整体收敛性，即对初始点的要求不高

收敛速度：线性收敛

因此，虽然最速下降法具有很好的整体收敛性，但由于其收敛速度太慢并不是很好的实用算法，但是有一些有效算法是基于它改进的，如批量梯度下降，随机梯度下降等，以后整理。

Newton法

最速下降法的本质是用线性函数去近似目标函数，因此要想快速得到，需要考虑对目标函数的高阶逼近。牛顿法就是通过二次模型近似目标函数得到的，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。先建立一个这样的宏观认识，下面详细说。

Newton法解方程

牛顿法是一种利用迭代思想近似求解方程的方法，使用函数 f ( x ) 的泰勒级数的前面几项来寻找方程 f ( x ) = 0 的根。取百度百科的原理部分如下：

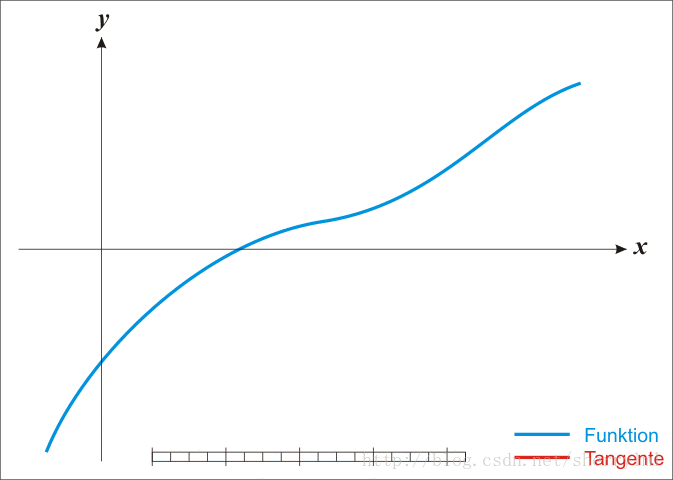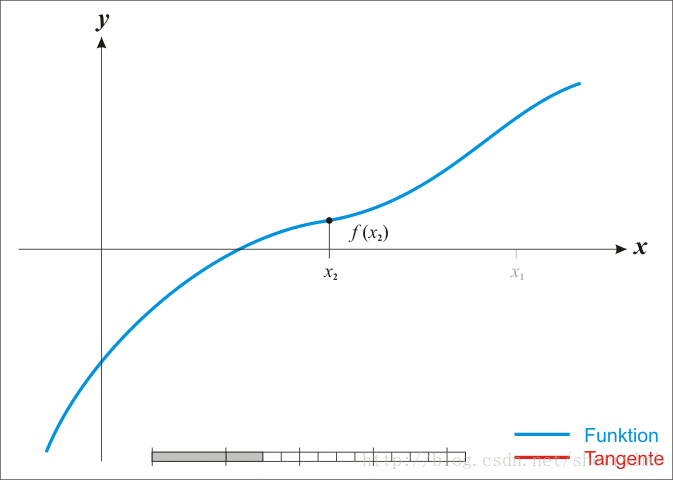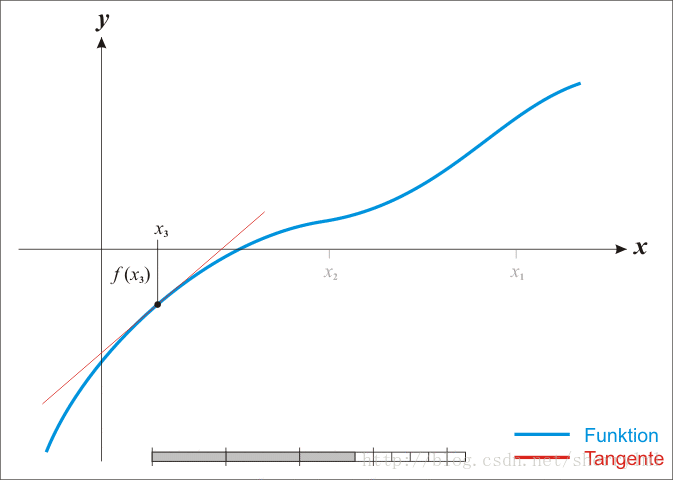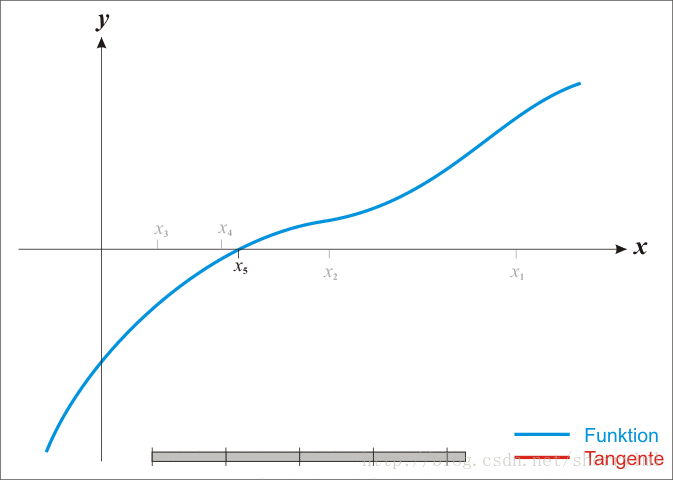
由于牛顿法是基于当前位置的切线来确定下一次的位置，所以牛顿法又被很形象地称为是”切线法”。牛顿法的搜索路径（二维情况）如下图所示：
牛顿法搜索动态示例图： [reference: http://www.cnblogs.com/maybe2030/p/4751804.html ]

Newton法最优化

由前面我们知道我们的任务是最小化目标函数$f$，因此可以转化为求解函数f的导数$f^{'}=0$的问题，这样就可以把优化问题看成方程（$f^{'}=0$）的求解问题。

推导：
对目标函数$f(\mathbf x)$在$\mathbf x_k$进行泰勒级数展开,忽略二阶导之后的高阶项
$f(\mathbf x) \approx q_k(\mathbf x)=f_k+\mathbf g_k^T(\mathbf x-\mathbf x_k)+\frac12(\mathbf x-\mathbf x_k)^T\mathbf G_k(\mathbf x-\mathbf x_k)$
矩阵的形式你可能看起来有点懵，其实对应我们常见的形式就是

根据上一节解方程的过程我们知道下一次近似的$\mathbf x_{k+1}$应满足$\nabla q_k(\mathbf x_{k+1})=0=\mathbf g_k + \mathbf G_k(\mathbf x_{k+1}-\mathbf x_k)$
$\mathbf x_{k+1}=\mathbf x_k-\mathbf G_k^{-1}\mathbf g_k$
在实际应用中，求逆运算太复杂，我们一般通过解方程$G_kp=-g_k$来确定.

基本步骤：
每一步迭代过程中，通过解线性方程组得到搜索方向，然后将自变量移动到下一个点，然后再计算是否符合收敛条件，不符合的话就一直按这个策略（解方程组→得到搜索方向→移动点→检验收敛条件）继续下去。

优缺点：
收敛速度快：二阶收敛速度（收敛速度明显快过梯度下降）

1. 局部收敛，只有当初始点充分接近极小点时才能保证收敛，即使Newton法收敛也不一定收敛到极小点，还可能是鞍点或极大点。
2. 牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂，且G还可能是奇异矩阵。
3. 虽然我们提到可以使用解方程$G_kp=-g_k$来确定下一个移动点，但是这个方程有可能是病态的
   ref: http://www.codelast.com/%e5%8e%9f%e5%88%9b-%e5%86%8d%e8%b0%88-%e7%89%9b%e9%a1%bf%e6%b3%95newtons-method-in-optimization/

因为牛顿法的收敛速度确实很快，因此人们针对牛顿法的缺点做出了各种改进版本，如阻尼牛顿法，Goldstein-price修正等，上面这个参考连接中有提到。

共轭方向法

共轭方向法是介于梯度下降法和Newton法之间的方法，为什么这么说呢？我们根据Newton法的介绍可以知道对于二次函数，Newton法只需要迭代一次就可以得到极小值（当然假设是存在的），而最速下降法需要迭代无穷多次，但是Newton法的计算代价太大，因此我们放松要求，只要找到在有限次迭代后可得到二次函数极小点的算法就是有效的算法，这种算法称为具有二次终止性。

理论基础：共轭方向及其性质

设$\mathbf G$为n阶正定矩阵，$\mathbf p_1,\mathbf p_2,...,\mathbf p_k$为n维向量组，如果$\mathbf p_i^T\mathbf G\mathbf p_j = 0,\qquad i,j=1,2,...,k, i\neq j$
则称向量组$\mathbf p_1,\mathbf p_2,...,\mathbf p_k$关于$\mathbf G$共轭。如果$\mathbf G$为单位矩阵I ，则$\mathbf p_1,\mathbf p_2,...,\mathbf p_k$是正交的。

重要定理：
对正定二次函数$f(\mathbf x)=\frac12 \mathbf x_T\mathbf Gx+\mathbf b^T\mathbf x+\mathbf c$，由任意初始点开始，依次进行k次精确一维搜索，$\mathbf x_{i+1}=\mathbf x_i+\alpha_i\mathbf p_i,\quad i=1,2,...,k$，则$\mathbf g_{k+1}^T\mathbf p_i=0,\quad i=1,2,...,k，\quad \mathbf x_{k+1}$是二次函数在k维超平面上的极小点，当k=n时,为$R^n$上的极小点
通俗来说，$\color {red} {就是当前迭代点的梯度g与前面所有的搜索方向p都正交}$

这里的证明需要知道很多性质和定理，就不一一说明了，找一本最优化的书看可能比较好，或者参考连接2中的博客有写的比较好懂。

基本思想

如果第k次迭代所取的方向与前面各次迭代所取的方向关于G共轭，则从任意初始点出发，对二次函数进行精确的一维搜索，至多经过n次迭代就可以得到极小点
公式打起来一下午就没有了。。。偷个懒，这里借用下codelast（参考连接2）的：

关键：如何选取共轭方向$p_k$(对应上面这个截图的$d_k$)，不同的选法会产生不同的共轭方向法，下面介绍共轭梯度法，因为它用到了目标函数的梯度

共轭梯度法

共轭梯度法是一种特殊的共轭方向法。由于其存储量小，可以用来求解大规模无约束优化问题。
。。。

拟Newton法

参考

1. 《最优化方法》解可新，韩健，林书联 编
2. http://www.codelast.com/ （感谢博主的文章）