镇文图
☆说在前面☆
本章内容应该紧跟着第三章的知识整理发布的，但是中间出了点问题，所以鸽了。不定积分的公式你要说有多少，那是真的多。我在一本教材的附录上找到了不定积分表，里面有140多个公式。最初我是打算把这些公式从头到尾都推导一遍，发现工作量大得不可思议，而且有些我根本就推导不出来！其实，不定积分的核心知识点并不多，那些拓展性的结论其实没必要记忆(反正也记不住，考试的时候还是得重新推导)。本次知识整理我将对不定积分这一章节的知识点进行整理，力争保留最精华的部分。
一、核心知识点
1.不定积分的概念
如果一个函数F(x)的导数是f(x)，那么就称F(x)是f(x)的【一个】原函数。f(x)所有原函数的集合称为f(x)的不定积分，记作∫f(x)dx=F(x)+C。
2.基本积分公式
基本积分公式
其中基本积分公式(一)是由基本求导公式直接得到的，基本积分公式(二)是由第一类换元法推导出来的。
3.不定积分的性质
加可拆，系数可提。∫[kf(x)+g(x)]dx=k∫f(x)dx+∫g(x)dx。
4.求不定积分之第一类换元法(凑微分法)
∫f[g(x)]·g'(x)dx=∫f[g(x)]d[g(x)]dx=F[g(x)]+C
注意到不定积分的表示式“∫f(x)dx”中有一个微分符号d，那么也就是说它符合微分的运算法则【d[f(x)]=f'(x)dx】。如果f(x)中的一个部分很好积分，那么就可以把这个部分移到微分符号的右边去。比如∫(sin x·cos x)dx，容易知道cos x的一个原函数是sin x，于是原式子化为∫(sin x)d(sin x)，令u=sin x，得原式=∫udu，很容易就知道原式等于(1/2)u²，再还原即得∫(sin x·cos x)dx=(1/2)sin²x。
第一类换元法是求不定积分的核心方法，即使用到后面的第二类换元法和分部积分法，也离不开第一类换元法。其中，基本微分性质必须熟悉：dφ(x)=(1/a)d[aφ(x)+b]。
5.求不定积分之第二类换元法
第一类换元法的核心是令u=g(x)，与之相反，第二类换元法的核心是令x=g(u)。
∫f(x)dx=∫f[g(u)]d[g(u)]=∫f[g(u)]g'(u)du
化成这样的形式之后，就好用第一类换元法求不定积分了，最后代入u=g^(-1)(x)(g^(-1)(x)是g(x)的反函数)即可得到结果。根据g(x)的形式，第二类换元法又分为了三种类型：三角代换、根式代换和倒代换。
①三角代换。我这里用一道例题来说明。
例如：∫sqrt(1-x²)dx。
看到这个平方相减我们联想到三角恒等式sin²x+cos²x=1，所以我们令x=sin t(注意t的定义域！因为x∈[-1,1]，所以t∈[-π/2,π/2])。
原式=∫sqrt(cos²t)d(sin t)=∫cos²tdt=(1/2)∫(1+cos 2t)dt。
【利用二倍角公式cos 2θ=2cos²θ-1得到】
利用不定积分的加可拆性质，得到原式=(1/2)t+(1/4)sin 2t。(积分常数最后再加)
这时候我们已经求出了代换后的不定积分的结果。最后一步就是回代。由x=sin t我们可以得到t=arcsin x。直接将t代入，有原式=(1/2)arcsin x+(1/4)sin(2arcsin x)。
而sin(2arcsin x)=2sin(arcsin x)cos(arcsin x)=2x·sqrt(1-x²)。
所以∫sqrt(1-x²)dx=(1/2)arcsin x+(x/2)sqrt(1-x²)+C。
以下是常用的三角代换技巧：
①看到sqrt(a²-x²)时，可作代换x=a·sin t(|t|≤π/2)；
因为我们有三角恒等式1-sin²x=cos²x。
②看到sqrt(a²+x²)时，可作代换x=a·tan t(|t|
因为我们有三角恒等式1+tan²x=sec²x。
③看到sqrt(x²-a²)时，可作代换x=a·sec t(0
因为我们有三角恒等式sec²x-1=tan²x。
需要注意的是，我们老师特别强调了一点，使用三角代换要画三角形。这是因为当代换较为复杂时，我们最好用辅助三角形法进行变量还原，否则极易出错。仍然以上一道题为例，画出如下图的辅助三角形，代换变量之间的关系会非常清楚：
三角代换要画辅助三角形
如果说x=sin t，那么根据三角函数的定义，有sin t=x/1(对边比斜边)，反过来我们就会知道x/1对应的是t的正弦值(所以才根据这个得到t=arcsin x)。别看这个简单，但有时候正弦余弦正切以及它们的反函数真的是理不清楚，所以有必要画辅助直角三角形。
②倒代换。这种代换的形式一般为x=1/u，通常用在求分母次数比分子次数要高的不定积分中。例如∫1/[x(6+x^8)]dx，分母中有x的8次方这根本没法直接求。我们通过倒代换，弄出可以凑微分的因子就好办了。解题过程：(图中t=1/x与x=1/t是一样的，但我想表达的其实是后者，写错了[笑哭])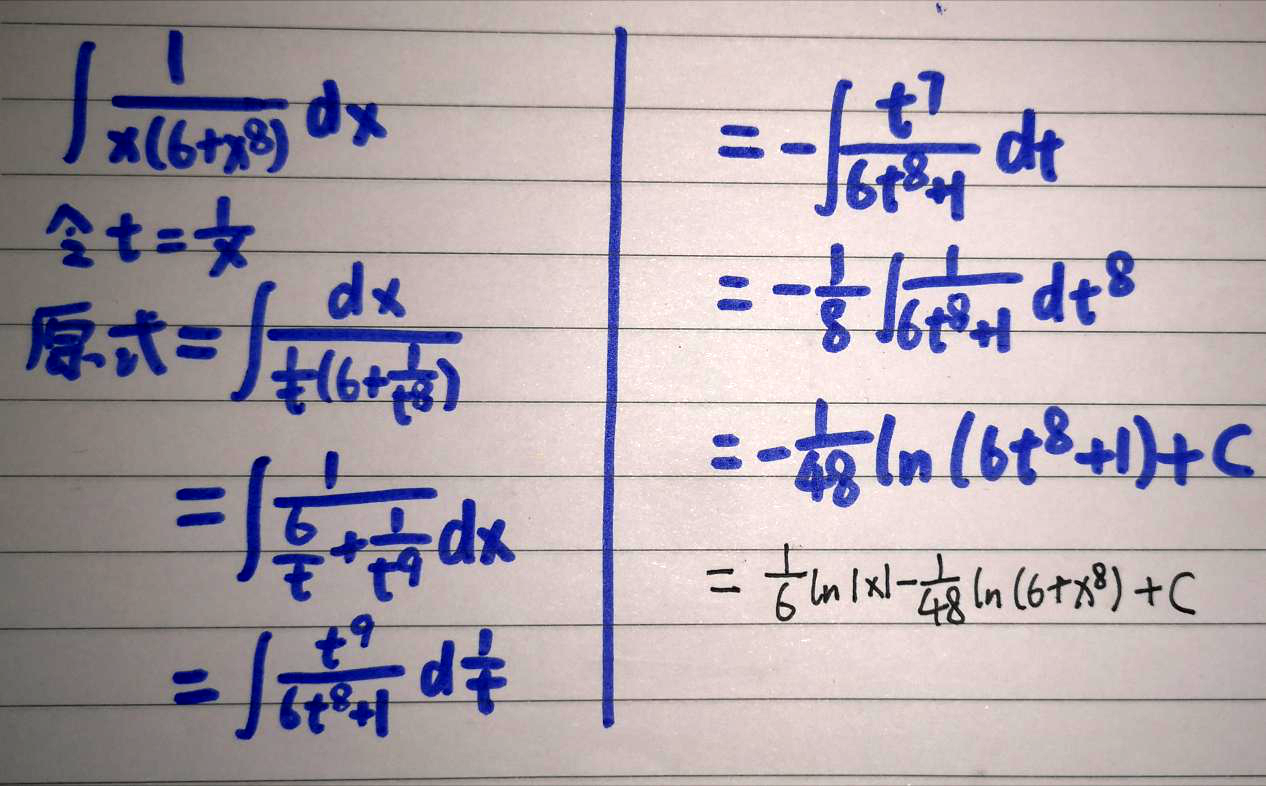
倒代换
③根式代换。这种代换一般直接将整个根式替换为中间变量u(不是x=g(u)的形式，但仍然属于第二类换元法)。例如计算∫1/[sqrt(1+e^x)]dx，直接令u=sqrt(1+e^x)，接下来的就好办了。(过程略)
6.求不定积分之分部积分法
由两个函数乘积的求导法则很容易推导出分部积分法公式：
设u=u(x)，v=v(x)，则有∫uv'dx=uv-∫u'vdx。
分部积分法可以说是最有意思的一种积分方法了。比如求∫ln xdx，原式=xln x-∫xd(ln x)=xln x-∫1dx=x·ln x-x。
注意分部积分法有两类特殊的用法。一是有一类含三角函数的不定积分在若干次使用分部积分法求不定积分之后会回到原来的形态，这时候就像解方程一样把它解出来就好；二是对与某些形如∫([f(x)]^n)dx的积分可以用它导出其递推公式(关于这个，下文有一个关于n次方三角函数的不定积分的推导，可以参考)。
二、技巧与运用
1.有理函数和可化为有理函数的积分
这部分是最难的，我至今也没有完全弄清楚。虽然专栏没啥人看，但还是有人看，本着对自己对读者负责任的态度，我！必！须！讲！清！楚！
对于有理函数(就是那种特别复杂的分式)，可以通过部分分式分解将其化为最简分式和，然后利用积分的加可拆性质求出其积分；对于三角函数和简单无理函数的积分，通过变量代换将其化为有理函数的积分即可。
①部分分式分解。部分分式分解又分两种情况，一是分母因式分解后每项都不一样(即每个因子的次数都是1)，二是分母因式分解后出现因子次数大于1的项(即有因子重复)。下面我会各举一个例子来说明两种情况怎么做(由于直接打出来排版复杂且不直观，故拍草稿照片)。
情况一：
部分分式分解
情况二：
部分分式分解
过程解释在草稿中已写出，但如果还有不懂的地方，欢迎评论留言。
②三角函数有理式的积分。所有三角函数都可以用sin x和cos x表示，所以含三角函数的有理式总可以记为只含sin x和cos x的式子。利用万能代换公式u=tan(x/2)便能将其化为有理函数的积分。
sin x=2sin(x/2)cos(x/2)/[cos²(x/2)+sin²(x/2)]=2u/(1+u²)
cos x=(1-u²)/(1+u²),tan x=2u/(1-u²),dx=[2/(1+u²)]du
其中sin x的推导过程如下。tan x由二倍角公式tan 2θ=2tanθ/(1-tan²θ)推导出，cos x可由三角公式tan x=sin x/cos x推出。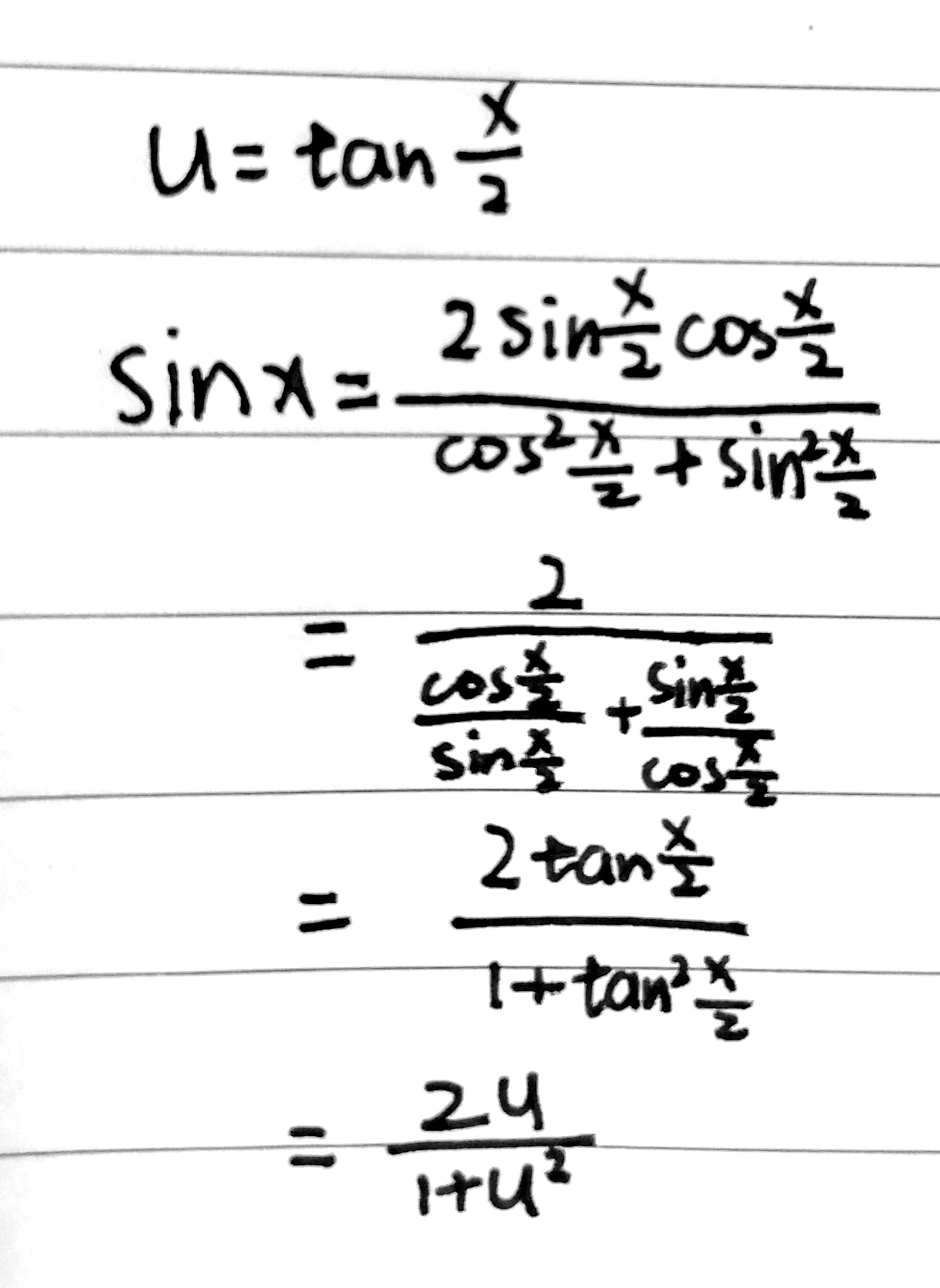
万能代换推导
下面我以一道题为例来演示万能代换怎么用：
万能代换的应用
需要注意的是，万能公式虽然万能，但计算量比较大。如果能通过观察发现待积分函数中可化简的地方，可以更简便地计算出不定积分。
③简单无理函数的积分。一般都是令整个根式等于中间变量来简化积分。若f(x)中含有根式函数g(x)，那么直接令u=g(x)计算积分,最后根据反函数求出x=g^(-1)(u)，再代入求解。
2.正弦/余弦函数的n次方的积分及其推导
对于sin x、cos x的n次方的积分系列，有如下公式(递推公式)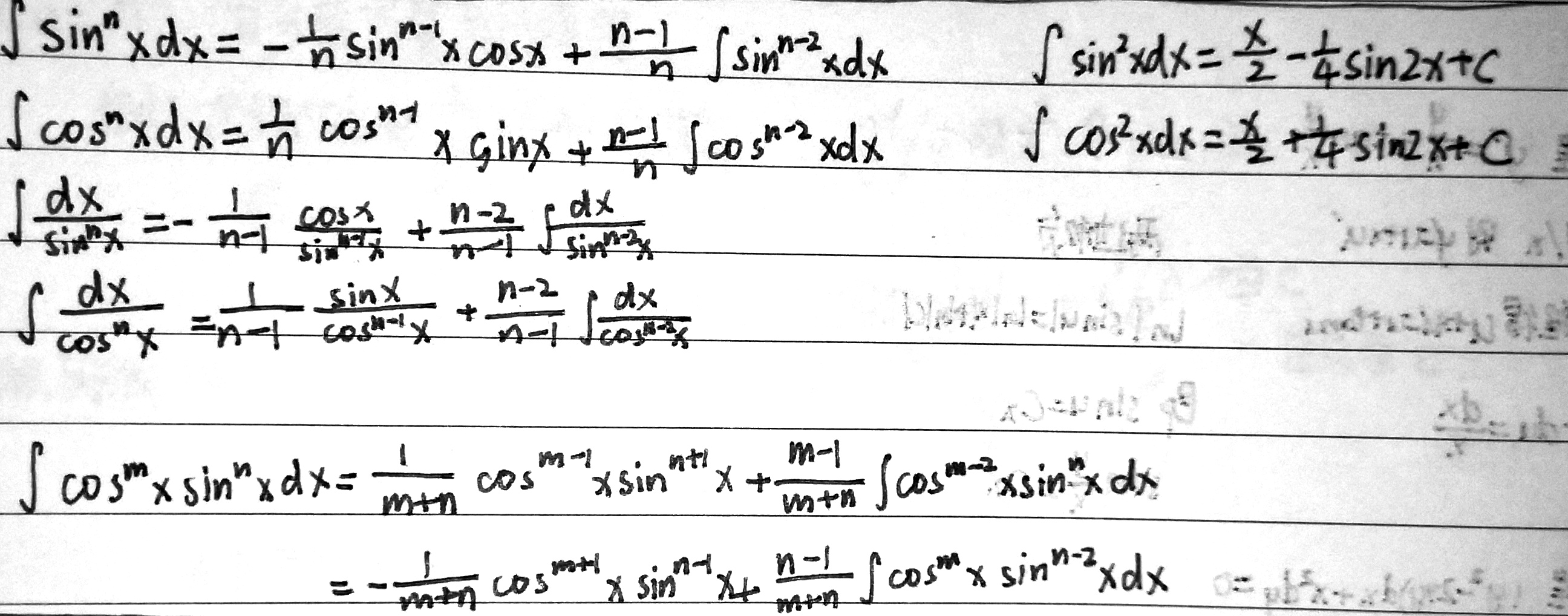
sin x、cos x的n次方的积分系列公式
其中第一个公式的推导过程如下：
第一个公式的推导过程
第三个公式的推导过程如下：
第三个公式的推导过程
其他公式可以用类似的方法得到。
3.三角函数系列求导/积分公式
三角函数系列求导/积分公式
4.三角函数n次方系列积分公式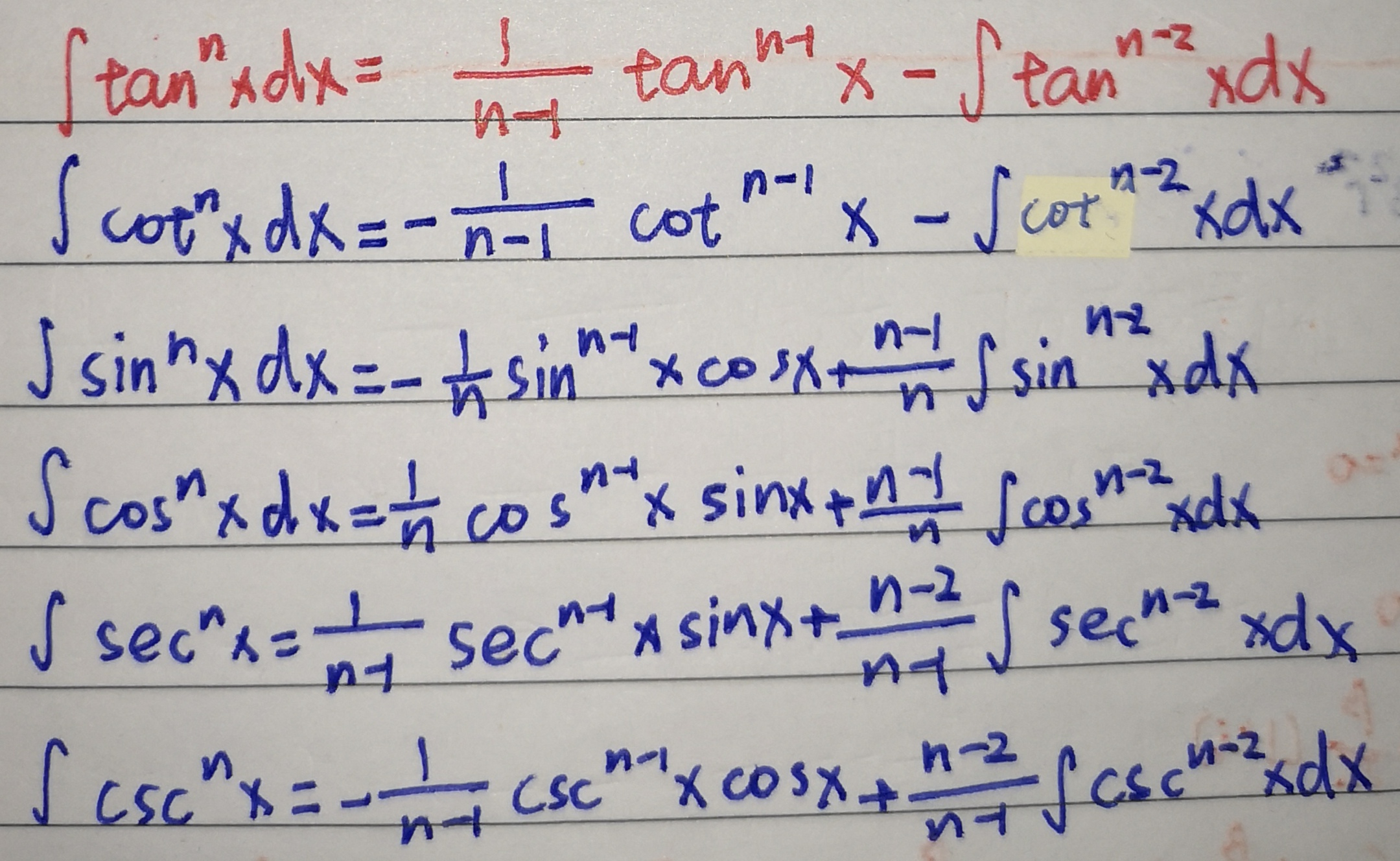
三角函数n次方系列积分公式
三、归纳与总结
1.来自课本的本章小结：
第四章归纳总结-1
第四章归纳总结-2
2.官方劝退？不定积分的特点决定了它的运算远比导数/微分运算要困难得多，而且方法技巧众多(本专栏只整理了核心方法)。不过不要怕，只要不断练习，就能熟悉这些技巧，做到得心应手。
“官方劝退”
3.特别注意：对初等函数来说，在其定义区间上，它的原函数一定存在，但原函数不一定是初等函数，如∫e^(-x^2)dx，∫[(sin x)/x]dx等，都不是初等函数，这种情况俗称“积不出来”。
4.求不定积分一定不要忘记加上积分常数！
否则会扣分，不值得！重要的事情说三遍：
求不定积分不要忘记+C！
求不定积分不要忘记+C！
求不定积分不要忘记+C！
当然关于这个有一个段子。有一种饮料就叫做+C，于是有人说，考高数的时候放一瓶+C，时时刻刻提醒自己不要忘记+C[笑哭]……
求不定积分不要忘记+C！
(本章完~)