【C语言】案例四十三 幻方（魔方阵）

案例分析
将从1到n方的的自然数，排列成纵横各有n个数的矩阵，使每行，每列，每条主对角线上的n个自然数之和都相等，这样的矩阵就是魔方阵，也称作幻方，本案例要求编写程序，实现奇数的幻方。

案例设计

1. 矩阵的行数，列数，矩阵中的元素的数量都由n决定，在程序中设置scanf()函数，由用户手动控制幻方的规模。因为本案例为奇数幻方，如果输入的数不是奇数，则使用goto语句回到输出函数之前；
2. 因为本案例中元素数量不稳定，则使用malloc函数动态申请存储空间
3. 幻方中的数据按行序优先存储在malloc函数开辟的空间中，在输出时，每输出n个数据，进行一次换行。
4. 将所有的操作封装在一个函数中，在主函数中调用该函数，幻方输出后，使用free函数释放函数中申请的堆空间。

完整代码

#include <stdlib.h>
#include <stdio.h>
#include <time.h>

//函数声明
void array();

int main()
{
	
	array();  //调用函数
	system ("pause");
	return 0;

}
	
//函数定义
void array()
	{
		int n;
		int	i,j,idx,num,MAX;
		int* M;    //定义一个一维数组指针，按行优先存储矩阵中的元素
		printf("请输入n:");
        input:
		scanf("%d",&n);
		if (n % 2 == 0)  // n是偶数，则重新输入
		{
			printf("n不为奇数，请重新输入：");
			goto input;
		}
		MAX = n*n;      //幻方中的最大值，也是元素个数
		M = (int*)malloc(sizeof(int)*MAX);  //分配存储空间
		M[n / 2] = 1;   //获取数值为1的列表
		i = 0;
		j = n / 2;
		//从2开始确定每个数的存放位置
		for(num = 2;num <= MAX; num++)
		{
			i = i - 1;
			j = j + 1;
			if((num - 1) % n == 0)  //当前数是n 的倍数
			{
				i = i + 2;
				j = j - 1;
			}
			if(i < 0)       // 当前数在第零行
			{
				i = n - 1;
			}
			if(j > n - 1)   //当前数在最后一列，即n - 1列
			{
				j = 0;
			}
			idx = i*n + j;  //根据二维数组下标与元素的对应关系
			                //找到当前在数组中的存放位置

			M[idx] = num;
		}
		//打印生成幻方
		printf("生成的%d阶幻方：",n);
		idx = 0;
		for(i = 0;i < n;i++)
		{
			printf("\n");    //每n个数据为一行
			for(j = 0;j <n;j++)
			{
				printf("%3d",M[idx]);
				idx++;
			}
		}
		printf("\n");   
		free(M);
	}

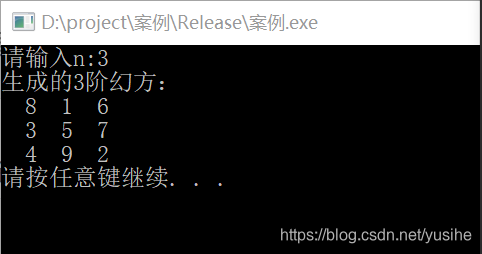
代码运行如下：