一种积分变换,它来源于函数的傅里叶积分表示。积分 (1) 称为ƒ 的傅里叶积分。周期函数在一定条件下可以展成傅里叶级数,而在(-∞,∞)上定义的非周期函数ƒ,显然不能用三角级数来表示。但是J.-B.-J.傅里叶建议把ƒ表示成所谓傅里叶积分的方法。
傅里叶变换在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中,傅里叶变换的典型用途是将信号分解成幅值谱——显示与频率对应的幅值大小)。
傅里叶变换(fft)matlab程序一
Fs = 128; % 采样频率
T = 1/Fs; % 采样时间
L = 256; % 信号长度
t = (0:L-1)*T; % 时间
x = 5 + 7*cos(2*pi*15*t - 30*pi/180) + 3*cos(2*pi*40*t - 90*pi/180); %cos为底原始信号
y = x + randn(size(t)); %添加噪声 figure; plot(t,y)
title(‘加噪声的信号’)
xlabel(‘时间(s)’)
N = 2^nextpow2(L); %采样点数,采样点数越大,分辨的频率越精确,N》=L,超出的部分信号补为0
Y = fft(y,N)/N*2; %除以N乘以2才是真实幅值,N越大,幅值精度越高
f = Fs/N*(0:1:N-1); %频率
A = abs(Y); %幅值
P = angle(Y); %相值
figure;
subplot(211);plot(f(1:N/2),A(1:N/2)); %函数fft返回值的数据结构具有对称性,因此我们只取前一半
title(‘幅值频谱’);
xlabel(‘频率(Hz)’);
ylabel(‘幅值’);
subplot(212);
plot(f(1:N/2),P(1:N/2));
title(‘相位谱频’);
xlabel(‘频率(Hz)’);
ylabel(‘相位’);
傅里叶变换(fft)matlab程序二
tp=0:2048; % 时域数据点数
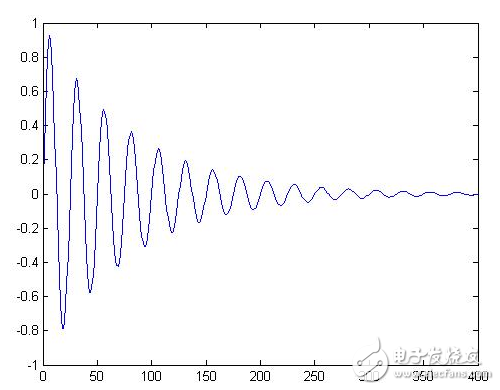
N yt=sin(0.08*pi*tp).*exp(-tp/80); % 生成正弦衰减函数
plot(tp,yt), axis([0,400,-1,1]), % 绘正弦衰减曲线
t=0:800/2048:800; % 频域点数Nf
f=0:1.25:1000;
yf=fft(yt); % 快速傅立叶变换
ya=abs(yf(1:801)); % 幅值
yp=angle(yf(1:801))*180/pi; % 相位 y
r=real(yf(1:801)); % 实部
yi=imag(yf(1:801)); % 虚部
figure subplot(2,2,1)
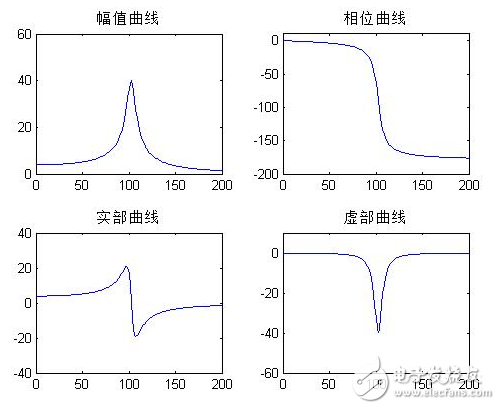
plot(f,ya),axis([0,200,0,60]) % 绘制幅值曲线
title(‘幅值曲线’)
subplot(2,2,2)
plot(f,yp),axis([0,200,-200,10]) % 绘制相位曲线
title(‘相位曲线’)
subplot(2,2,3)
plot(f,yr),axis([0,200,-40,40]) % 绘制实部曲线
title(‘实部曲线’)
subplot(2,2,4)
plot(f,yi),axis([0,200,-60,10]) % 绘制虚部曲线
title(‘虚部曲线’)
结果