刚接触李超线段树不久,感觉还是很容易掌握的,写一篇简单的博客记录一下
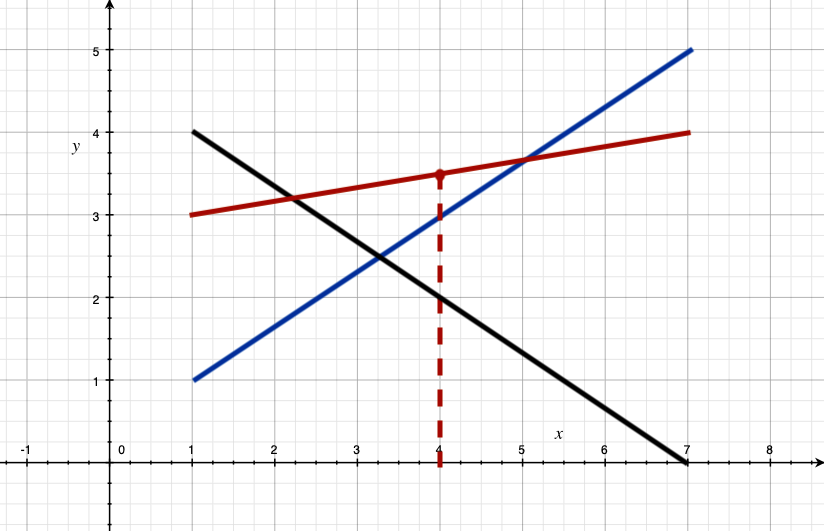
李超线段树解决的是这样一类问题:给定二维平面上的一些线段,求x = p o s x=posx=pos与这些线段的交点最高的那个点,例如下面这个图,给定p o s = 4 pos=4pos=4,则答案就是那个虚线与红线的交点
顾名思义,李超线段树首先是棵线段树,其核心是维护每个区间的“最优势线段”,即在每个区间的中点处最高的线段。
为了更好理解李超线段树,先介绍查询步骤更好一点
查询步骤
设查询的位置为p o s pospos,对于线段树上的每一个包含p o s pospos的区间,取所有这些区间记录的最优势线段的对应x = p o s x=posx=pos下的最高点插入线段步骤
设待插入的线段左端点L LL,右端点R RR,其函数表达式为f ( x ) f(x)f(x),对于线段树上的每一个完全被包含在区间[ L , R ] [L,R][L,R]内的区间,更新该区间的“最优势线段”,分类讨论如下
若该区间还没有记录最优势线段,则记录最优势线段并返回
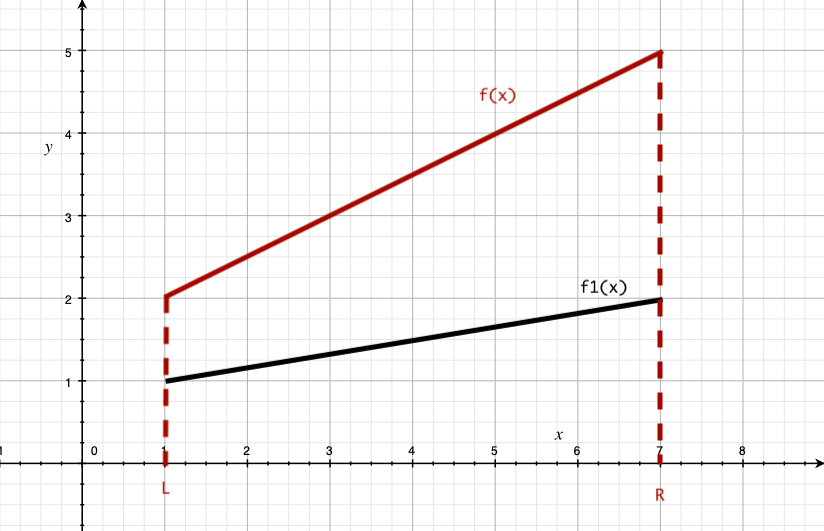
设该区间记录的最优势线段函数表达式为f 1 ( x ) f_1(x)f1(x),若f ( L ) > f 1 ( L ) f(L)>f_1(L)f(L)>f1(L)且f ( R ) > f 1 ( R ) f(R)>f_1(R)f(R)>f1(R),则更换最优势线段为f 1 ( x ) f_1(x)f1(x),并返回
若是两线段交叉的情况,另m i d = ( L + R ) 2 mid=\frac{(L+R)}{2}mid=2(L+R),若f ( m i d ) > f 1 ( m i d ) f(mid)>f_1(mid)f(mid)>f1(mid),则交换f ( x ) f(x)f(x)与f 1 ( x ) f_1(x)f1(x),由于交换后必有f 1 ( m i d ) ≥ f ( m i d ) f_1(mid)\geq f(mid)f1(mid)≥f(mid),继续讨论f ( x ) f(x)f(x)与f 1 ( x ) f_1(x)f1(x)的交点横坐标x xx情况
- x > m i d x>midx>mid
这时用劣势线段( ((也就是线段f ( x ) ) f(x))f(x)) 去继续更新右区间,注意此时的f ( x ) f(x)f(x)可能是交换后的【如果不是交换后的那么显然要去更新右区间】,其实这并不影响,因为如果是交换后的,那么上一次插入交换前的那个线段的时候,更新完当前区间就返回了,并没有更新右区间,而当交换后,如果不用劣势线段去跟新右区间,将丢失劣势线段的信息,而对于区间[ x , R ] [x,R][x,R]内的点来说,这条劣势线段才是取的最高的那条,所以必须用劣势线段去更新右区间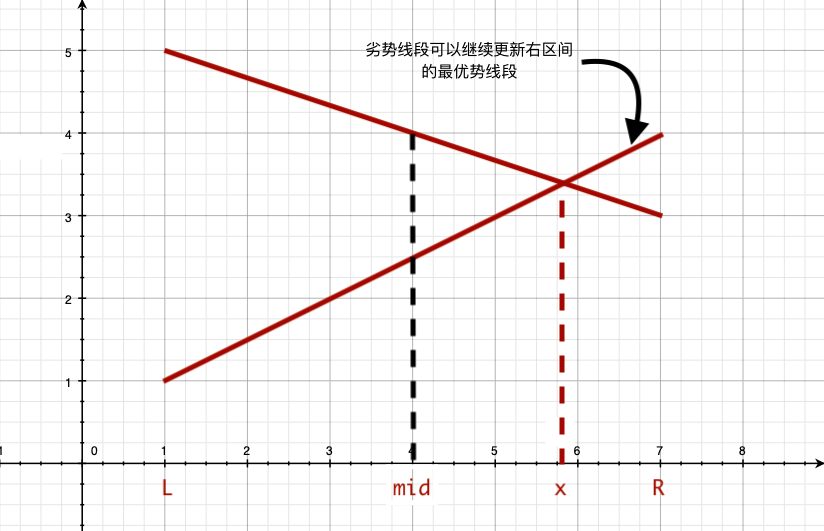
- x < m i d x<midx<mid
同上分析可知需要用劣势线段去更新左区间 - x = m i d x=midx=mid
当前区间最优势线段可以不更新【因为中点函数值都一样】,但是得更新左区间或者右区间,具体更新哪一个区间根据插入的线段在哪边更高就更新哪边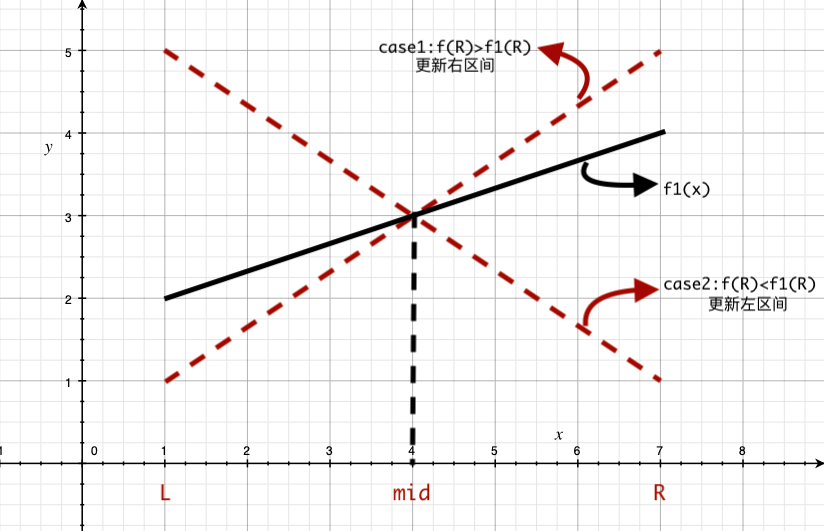
- x > m i d x>midx>mid
struct line{
double k,b;
int l,r,flag; //l,r表示线段的左端点和右端点,而线段树的左端点和右端点是不显示存储的
line(double a=0,double c=0,int d=0,int e=0,int f=0){
k=a;b=c;l=d;r=e;flag=f;
}
}seg[maxn<<2];
struct segment_tree{
inline double calc(line l1,int pos) {return l1.k*pos+l1.b;} //kx+b
inline int cross(line l1,line l2) {return floor((l1.b-l2.b)/(l2.k-l1.k));} //l1 l2交点
void build(int le,int ri,int id){
seg[id].l=1;seg[id].r=50000;seg[id].flag=0;
if(le==ri) return;
int mid=(le+ri)>>1;
build(le,mid,id<<1);build(mid+1,ri,id<<1|1);
}
void insert(int le,int ri,int id,line ins){ //le,ri为需要维护的区间,id为线段树区间编号,ins为需要插入的线段
if(ins.l<=le&&ins.r>=ri){
if(!seg[id].flag) {seg[id]=ins;seg[id].flag=1;}
else if((calc(ins,le)-calc(seg[id],le))>eps&&(calc(ins,ri)-calc(seg[id],ri))>eps) {seg[id]=ins;}
else if((calc(ins,le)-calc(seg[id],le))>eps||(calc(ins,ri)-calc(seg[id],ri))>eps){
int mid=(le+ri)>>1;
if(calc(ins,mid)-calc(seg[id],mid)>eps) swap(seg[id],ins);
if(cross(seg[id],ins)-mid<-eps) insert(le,mid,id<<1,ins);
else if(cross(seg[id],ins)-mid>eps) insert(mid+1,ri,id<<1|1,ins);
else{
if(calc(seg[id],le)<calc(ins,le)) insert(le,mid,id<<1,ins);
else insert(mid+1,ri,id<<1|1,ins);
}
}
}else{
int mid=(le+ri)>>1;
if(ins.l<=mid) insert(le,mid,id<<1,ins);
if(ins.r>mid) insert(mid+1,ri,id<<1|1,ins);
}
}
double query(int le,int ri,int id,int pos){ //le,ri表示当前询问的区间,如果x=pos处没有对应的线段,会返回-inf
if(le==ri) return seg[id].flag?calc(seg[id],pos):-inf;
int mid=(le+ri)>>1;double res=seg[id].flag?calc(seg[id],pos):-inf;
if(pos<=mid) res=max(res,query(le,mid,id<<1,pos));
else res=max(res,query(mid+1,ri,id<<1|1,pos));
return res;
}
}tree;
Description

Input
第一行 :一个整数N NN ,表示方案和询问的总数。
接下来N NN行,每行开头一个单词“Q u e r y QueryQuery”或“P r o j e c t ProjectProject”。
若单词为Q u e r y QueryQuery,则后接一个整数T,表示B l u e M a r y Blue MaryBlueMary询问第T TT天的最大收益。
若单词为P r o j e c t ProjectProject,则后接两个实数S , P S,PS,P,表示该种设计方案第一天的收益S SS,以及以后每天比上一天多出的收益P PP。
1 < = N < = 1000001 < = T < = 500000 < P < 100 , ∣ S ∣ < = 1 0 6 1 <= N <= 100000 1 <= T <=50000 0 < P < 100,| S | <= 10^61<=N<=1000001<=T<=500000<P<100,∣S∣<=106
提示:本题读写数据量可能相当巨大,请选手注意选择高效的文件读写方式。
Output
对于每一个Q u e r y QueryQuery,输出一个整数,表示询问的答案,并精确到整百元(以百元为单位,
例如:该天最大收益为210 210210或290 290290时,均应该输出2 22)。没有方案时回答询问要输出0 00
Sample Input
10
Project 5.10200 0.65000
Project 2.76200 1.43000
Query 4
Query 2
Project 3.80200 1.17000
Query 2
Query 3
Query 1
Project 4.58200 0.91000
Project 5.36200 0.39000
Sample Output
0
0
0
0
0
题解
- 每一个方案随时间的变化规律都可以表示成一个直线方程,然后就是模版题了
- 注意描述中“一开始没有收到任何方案时,你可以认为每天的最大收益值是0 00”这句话还是有点歧义的,并不是说没有插入任何线段之前查询的话输出0 00,插入之后在所有方案中查询一个最高点。而是任何时间查询都可以是0 00,也就是可以不选择任何方案,所以就直接插入一个k = 0 , b = 0 k=0,b=0k=0,b=0的线段就行了
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
#define eps 1e-9
#define inf 0x3f3f3f3f
struct line{
double k,b;
int l,r,flag; //l,r表示线段的左端点和右端点,而线段树的左端点和右端点是不显示存储的
line(double a=0,double c=0,int d=0,int e=0,int f=0){
k=a;b=c;l=d;r=e;flag=f;
}
}seg[maxn<<2];
struct segment_tree{
inline double calc(line l1,int pos) {return l1.k*pos+l1.b;} //kx+b
inline int cross(line l1,line l2) {return floor((l1.b-l2.b)/(l2.k-l1.k));} //l1 l2交点
void build(int le,int ri,int id){ //这个操作好像没啥用233
seg[id].l=1;seg[id].r=50000;seg[id].flag=0;
if(le==ri) return;
int mid=(le+ri)>>1;
build(le,mid,id<<1);build(mid+1,ri,id<<1|1);
}
void insert(int le,int ri,int id,line ins){ //le,ri为需要维护的区间,id为线段树区间编号,ins为需要插入的线段
if(ins.l<=le&&ins.r>=ri){
if(!seg[id].flag) {seg[id]=ins;seg[id].flag=1;}
else if((calc(ins,le)-calc(seg[id],le))>eps&&(calc(ins,ri)-calc(seg[id],ri))>eps) {seg[id]=ins;}
else if((calc(ins,le)-calc(seg[id],le))>eps||(calc(ins,ri)-calc(seg[id],ri))>eps){
int mid=(le+ri)>>1;
if(calc(ins,mid)-calc(seg[id],mid)>eps) swap(seg[id],ins);
if(cross(seg[id],ins)-mid<-eps) insert(le,mid,id<<1,ins);
else if(cross(seg[id],ins)-mid>eps) insert(mid+1,ri,id<<1|1,ins);
else{
if(calc(seg[id],le)<calc(ins,le)) insert(le,mid,id<<1,ins);
else insert(mid+1,ri,id<<1|1,ins);
}
}
}else{
int mid=(le+ri)>>1;
if(ins.l<=mid) insert(le,mid,id<<1,ins);
if(ins.r>mid) insert(mid+1,ri,id<<1|1,ins);
}
}
double query(int le,int ri,int id,int pos){ //le,ri表示当前询问的区间
if(le==ri) return seg[id].flag?calc(seg[id],pos):-inf;
int mid=(le+ri)>>1;double res=seg[id].flag?calc(seg[id],pos):-inf;
if(pos<=mid) res=max(res,query(le,mid,id<<1,pos));
else res=max(res,query(mid+1,ri,id<<1|1,pos));
return res;
}
}tree;
int n,pos,l,r;
char opt[100];
double k,b;
int main()
{
scanf("%d",&n);tree.insert(1,50000,1,line(0,0,1,50000,1));
while(n--){
scanf("%s",opt+1);
if(opt[1]=='P'){
scanf("%lf %lf",&b,&k);
tree.insert(1,50000,1,line(k,b-k,1,50000,1));
}else{
scanf("%d",&pos);double res=tree.query(1,50000,1,pos);
printf("%d\n",(int)floor(res/100));
}
}
}
Description
小q qq有n nn只机器人,一开始他把机器人放在了一条数轴上,第i ii只机器人在ai的位置上静止,而自己站在原点。在这
之后小q qq会执行一些操作,他想要命令一个机器人向左或者向右移动x xx格。但是机器人似乎听不清小q qq的命令,事实
上它们会以每秒x xx格的速度匀速移动。看着自己的机器人越走越远,小q qq很着急,他想知道当前离他(原点)最远的
机器人有多远。具体的操作以及询问见输入格式。注意,不同的机器人之间互不影响,即不用考虑两个机器人撞在
了一起的情况。
Input
共有m mm个事件,输入将会按事件的时间顺序给出。第一行两个正整数n , m n,mn,m。接下来一行n nn个整数,第i ii个数是a i a_iai,表示
第i ii个机器人初始的位置(初始移动速度为0 00)。接下来m mm行,每行行首是一个非负整数t i t_iti,表示该事件点发生的时
刻(以秒为单位)。第二个是一个字符串S SS,代表操作的种类。数字与字符串之间用一个空格隔开。接下来的输入
按S SS的种类分类。若S SS是“c o m m a n d commandcommand”(不带引号),则接下来两个整数k i , x i k_i,x_iki,xi,表示小q qq对第k i k_iki个机器人执行了操作
,该机器人的速度将会被重置,变为向数轴正方向每秒移动x i x_ixi格(若x i x_ixi为负数就相当于向数轴负方向每秒移动∣ x i ∣ ∣x_i ∣∣xi∣格)。保证1 ≤ k i ≤ n 1\leq k_i\leq n1≤ki≤n。若S SS是“q u e r y queryquery”(不带引号),则你需要输出当前离原点最远的机器人有多远。保证t 1 ≤ t 2 ≤ t 2 ≤ . . . ≤ t m t_1 \leq t_2 \leq t_2 \leq...\leq tmt1≤t2≤t2≤...≤tm。(注:若同一时间发生多次操作,则按读入顺序依次执行)
Output
对于每个q u e r y queryquery询问,输出一行,包含一个整数表示正确的答案。C / C + + C/C++C/C++输入输出l o n g l o n g long\ longlong long时请用% l l d \%lld%lld。由于本题数
据量较大,建议不要使用c i n / c o u t cin/coutcin/cout进行输入输出。
Sample Input
4 5
-20 0 20 100
10 command 1 10
20 command 3 -10
30 query
40 command 1 -30
50 query
Sample Output
180
280
HINT
第一个命令执行时,各个机器人的位置为:− 20 , 0 , 20 , 100 −20,0,20,100−20,0,20,100。
第二个命令执行时,各个机器人的位置为:80 , 0 , 20 , 100 80,0,20,10080,0,20,100。
第一个询问时,各个机器人的位置为:180 , 0 , − 80 , 100 180,0,−80,100180,0,−80,100。
第三个命令执行时,各个机器人的位置为:280 , 0 , − 180 , 100 280,0,−180,100280,0,−180,100。
第二个询问时,各个机器人的位置为:− 20 , 0 , − 280 , 100 −20,0,−280,100−20,0,−280,100。
限制与约定
设 c o m m a n d commandcommand 的个数为 C CC,q u e r y queryquery 的个数为 Q QQ。(所以 C + Q = m C+Q=mC+Q=m)
对于所有的事件满足 0 ≤ t i ≤ 1 0 9 0 \leq ti \leq 10^90≤ti≤109,对于所有的 c o m m a n d commandcommand 满足 ∣ x i ∣ ≤ 1 0 4 ∣x_i∣\leq 10^4∣xi∣≤104。
对于所有的机器人满足 ∣ a i ∣ ≤ 1 0 9 ∣ai∣\leq 10^9∣ai∣≤109。
N , C ≤ 1 0 5 N,C \leq 10^5N,C≤105
Q ≤ 5 ∗ 1 0 5 Q \leq 5*10^5Q≤5∗105
Source
2015年集训队互测 By zhj
题意:
- 就是n个机器人在x轴上,给你所有机器人初始(0时刻)位置静止,然后给定两种操作,一个是让某个机器人以一定的速度开始运动,另一个操作是查询某个时刻距离原点最远的机器人的距离
题解
- 网上很多大神都是写的李超线段树+离散化,个人更喜欢动态开点
- 很容易看出来位置-时间是一个一次函数,所以就转化为李超线段树解决,首先需要明确的是后面的修改不会对前面的查询造成影响,因为t 1 ≤ t 2 ≤ . . . ≤ t m t_1\leq t_2\leq... \leq t_mt1≤t2≤...≤tm。所以考虑离线处理,即将所有线段插入到线段树中,然后再一起查询所有答案,注意有一个小的t r i k triktrik就是同一个时间对同一个点可能修改很多次,这时要注意保留最后一次修改的那个,这个d e b u g debugdebug数据我放在了代码后面,然后还有一个小技巧就是不用去维护最低的点,每次插入的时候同时插入一条关于x xx轴对称的线段就行了,这样就只用维护最大值了,分析一下时间复杂度,首先查询是O ( l o g 1 0 9 ) O(log 10^9)O(log109),修改过程也是O ( l o g 1 0 9 ) O(log 10^9)O(log109),总时间复杂度O ( m l o g 1 0 9 ) O(m log 10^9)O(mlog109),空间复杂度O ( m l o g 1 0 9 ) O(mlog 10^9)O(mlog109)
- 同时g e t getget到一个新操作
vector::insert() iterator insert ( iterator position, const T& x ); void insert ( iterator position, size_type n, const T& x ); template <class InputIterator> void insert ( iterator position, InputIterator first, InputIterator last ); 插入新的元素, 第一个函数,在迭代器指定的位置前插入值为x的元素 第二个函数,在迭代器指定的位置前插入n个值为x的元素 第三个函数,在迭代器指定的位置前插入另外一个容器的一段序列迭代器first到last 若插入新的元素后总得元素个数大于capacity,则又一次分配空间
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
#define eps 1e-9
#define inf 2e18
#define L 0
#define R 1e9
struct line{
long long k,b;
int l,r,flag,ls,rs; //l,r表示线段的左端点和右端点,而线段树的左端点和右端点是不显示存储的,ls左儿子,rs右儿子
line(long long a=0,long long c=0,int d=0,int e=0,int f=0,int g=0,int h=0){
k=a;b=c;l=d;r=e;flag=f;ls=g;rs=h;
}
}seg[maxn*30];
struct segment_tree{
int tot;
segment_tree() {tot=1;}
inline long long calc(line l1,int pos) {return l1.k*pos+l1.b;} //kx+b
inline long long cross(line l1,line l2) {return (long long)((l1.b-l2.b)/(l2.k-l1.k));} //l1 l2交点
void insert(int le,int ri,int id,line ins){ //le,ri为需要维护的区间,id为线段树区间编号,ins为需要插入的线段
if(ins.l>ins.r) return;
if(ins.l<=le&&ins.r>=ri){
if(!seg[id].flag) {
swap(seg[id],ins);seg[id].ls=ins.ls;seg[id].rs=ins.rs;
}
else if((calc(ins,le)-calc(seg[id],le))>eps&&(calc(ins,ri)-calc(seg[id],ri))>eps) {
swap(seg[id],ins);seg[id].ls=ins.ls;seg[id].rs=ins.rs;
}
else if((calc(ins,le)-calc(seg[id],le))>eps||(calc(ins,ri)-calc(seg[id],ri))>eps){
int mid=(le+ri)>>1;
if(calc(ins,mid)-calc(seg[id],mid)>eps) {
swap(seg[id],ins);seg[id].ls=ins.ls;seg[id].rs=ins.rs;
}
if(cross(seg[id],ins)-mid<-eps) {
if(!seg[id].ls) seg[id].ls=++tot;
insert(le,mid,seg[id].ls,ins);
}
else if(cross(seg[id],ins)-mid>eps) {
if(!seg[id].rs) seg[id].rs=++tot;
insert(mid+1,ri,seg[id].rs,ins);
}
else{
if(calc(seg[id],le)<calc(ins,le)) {
if(!seg[id].ls) seg[id].ls=++tot;
insert(le,mid,seg[id].ls,ins);
}
else {
if(!seg[id].rs) seg[id].rs=++tot;
insert(mid+1,ri,seg[id].rs,ins);
}
}
}
}else{
int mid=(le+ri)>>1;
if(ins.l<=mid) {
if(!seg[id].ls) seg[id].ls=++tot;
insert(le,mid,seg[id].ls,ins);
}
if(ins.r>mid) {
if(!seg[id].rs) seg[id].rs=++tot;
insert(mid+1,ri,seg[id].rs,ins);
}
}
}
long long query(int le,int ri,int id,int pos){ //le,ri表示当前询问的区间
if(le==ri) return calc(seg[id],pos);
int mid=(le+ri)>>1;long long res=calc(seg[id],pos);
if(pos<=mid&&seg[id].ls) res=max(res,query(le,mid,seg[id].ls,pos));
else if(pos>mid&&seg[id].rs) res=max(res,query(mid+1,ri,seg[id].rs,pos));
return res;
}
}tree;
char opt[100];
vector<pair<int,long long> > pos[maxn];
int a[maxn],n,m,x,t,que[3*maxn],cnt=0;long long k;
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=m;i++){
scanf("%d %s",&t,opt+1);
if(opt[1]=='q') que[++cnt]=t;
else{
scanf("%d %lld",&x,&k);
pos[x].push_back(make_pair(t,k));
}
}
for(int i=1;i<=n;i++) pos[i].insert(pos[i].begin(),make_pair(0,0)),pos[i].insert(pos[i].end(),make_pair(1e9+1,0));
for(int i=1;i<=n;i++){
long long last=a[i];
for(int j=0;j<pos[i].size()-1;j++){
long long b=last-pos[i][j].first*pos[i][j].second,k=pos[i][j].second;
tree.insert(L,R,1,line(pos[i][j].second,b,pos[i][j].first,pos[i][j+1].first-1,1));
tree.insert(L,R,1,line(-pos[i][j].second,-b,pos[i][j].first,pos[i][j+1].first-1,1));
last=pos[i][j].second*pos[i][j+1].first+b;
}
}
for(int i=1;i<=cnt;i++) printf("%lld\n",tree.query(L,R,1,que[i]));
}
/* 答案48
1 3
0
0 command 1 -3
0 command 1 -6
8 query
*/