Zhang, H., A. Zhou, Y. Hu, C. Li, G. Wang, X. Zhang, H. Ma, L. Wu, A. Chen and C. Wu (2021). Loki: improving long tail performance of learning-based real-time video adaptation by fusing rule-based models. Proceedings of the 27th Annual International Conference on Mobile Computing and Networking.
OnRL同作者
1. Motivation及解决思路
1.1 问题的提出
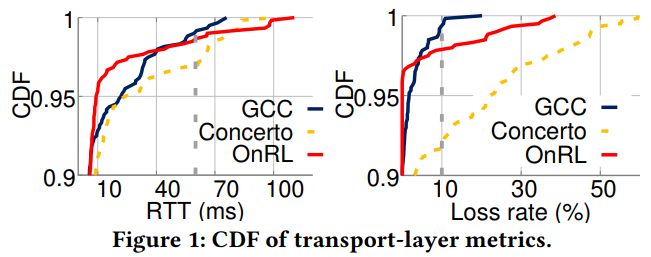
作者对现有基于学习的算法进行性能分析后发现:
- 这类算法确实可以在传输层上提高性能,但是这种性能提升却不能体现在QoE上。原因是传输层的性能参数呈长尾分布,即使算法的平均RTT很低,一两个时刻特别大的RTT仍会对QoE造成严重影响。
- 这类算法对于链路带宽的估计不够准确,常常给出高于实际带宽的估计值。
以上两个现象的根本原因来自于RL中自身的探索机制,即trial-and-error。这类算法往往以某些时刻的过度估计或者过低估计为代价以换取最大化的长期收益,这就会在性能上导致长尾效应。
1.2 解决思路
通过对启发式算法和基于RL的算法进行结合,提高算法的鲁棒性。
1)类似的解决思路及存在的问题
现有的结合思路大多采用"time-division"的方法,在时间线上异步调用两类算法。
OnRL--> 在检测到网络状况出现异常时,切换到启发式。
问题: 只有在网络拥塞产生后,OnRL才调用启发式。
Orca--> 交替使用启发式和RL算法。
问题: 在WebRTC中会导致比GCC更频繁的过估计和带宽利用不足的问题。它的效果主要依赖较大的缓冲区,但WebRTC中缓冲区小,所以表现不佳。
总结: 多路复用,异步调用的方式无法充分挖掘两类算法的能力。
2)难点
- 如何使启发式和RL之间相互兼容?
- 如何保证新的模型能获得上述两类算法各自的优势(启发式安全保守,RL向上探索快)?
3)本文方法
首先使用模仿学习的方法将GCC转化为神经网络的形式,作为其中一个actor。然后采用learning-based的方法单独训练一个actor。最后利用双注意力融合机制对两个actor的最后一层特征值进行融合,做出最终的码率决策。
2. 算法设计
2.1 Overview
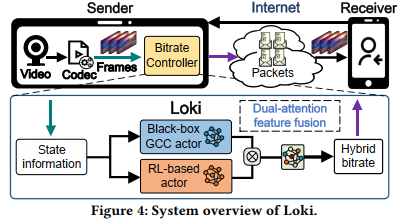
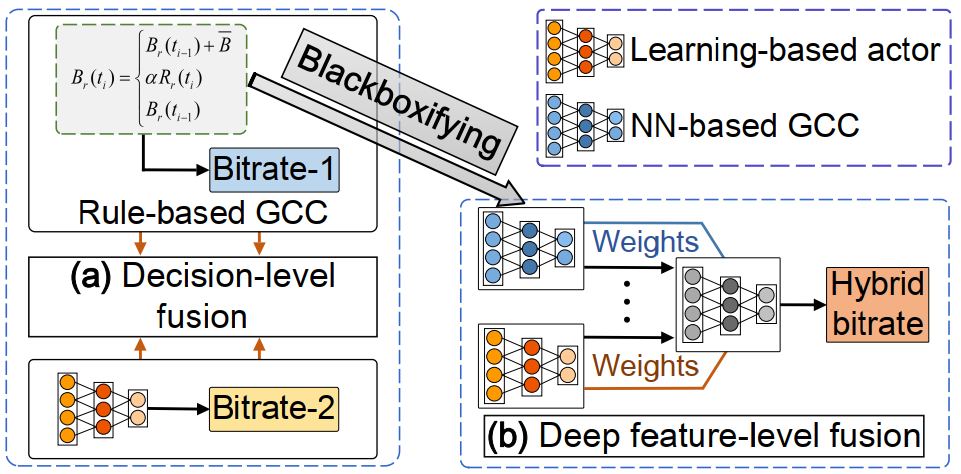
大致的思路是训练两个actor,然后对其进行融合:
- 利用GCC向上探索慢,向下退化快的特点。当网络状况变差时,让GCC在融合中占据更大权重,使此时的行动更加安全
- 网络状况恢复后,优先考虑向上探索速度快的RL-based actor,给予其更大权重保证带宽利用率。
2.2 GCC actor
1)为什么需要映射为NN?
- 原有的启发式算法是一个粗糙的分段函数,缺乏细粒度的特征表示能力
- 基于学习的算法构建在精细的神经网络之上,具有高层次的特征表示能力。
显然,两类算法在特征层面是不兼容的。为了让二者进行深度融合,考虑将GCC由“白盒”转换为“黑盒”,使其具备和learning-based model一样的抽象的特征表示能力。
2)如何实现?
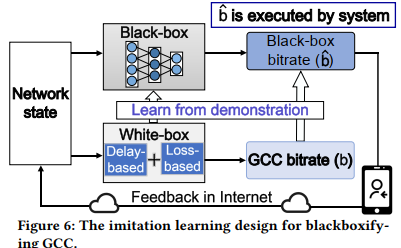
采用==模仿学习==的方法进行训练。
输入: I t = ( l ⃗ t , d ⃗ t ) I_{t}=\left(\vec{l}_{t}, \vec{d}_{t}\right)It=(lt,dt)
**输出:**列表{ 0.85 , 0.89 , 0.96 , 0.98 , 0.99 , 1.0005 , 1.001 , 1.0015 , 1.002 , 1.0025 } \{0.85,0.89,0.96,0.98,0.99,1.0005,1.001,1.0015,1.002,1.0025\}{0.85,0.89,0.96,0.98,0.99,1.0005,1.001,1.0015,1.002,1.0025}的概率分布P \mathcal{P}P,该列表表示增益系数。
- 训练阶段
b ∗ ^ = V [ max ( softmax ( P ) ) ] × b u ^ \hat{b^{*}}=\mathcal{V}[\max (\operatorname{softmax}(\mathcal{P}))] \times \hat{b_{u}}b∗^=V[max(softmax(P))]×bu^
从概率分布P \mathcal{P}P中选出值最大的一项对应的增益系数,与上一时刻的码率估计值相乘获得新的码率估计。将此估计值作用于环境。同时GCC作为专家也进行决策,用交叉熵作为损失函数。
注意:为了保证GCC actor较为保守的特性,引入加权系数在出现码率过估计的时候进行额外惩罚。
- 融合阶段
将网络中最后一层的概率分布作为维融合模块的输入。
2.3 RL-based actor
采用PPO
State:S t = ( l ⃗ t , j ⃗ t , d ⃗ t , t t ) S_{t}=\left(\vec{l}_{t}, \vec{j}_{t}, \vec{d}_{t}, t_{t}\right)St=(lt,jt,dt,tt)
Actor:A : { 0.7 M b p s , 0.83 M b p s , … , 1.87 M b p s , 2.0 M b p s } \mathcal{A}:\{0.7 \mathrm{Mbps}, 0.83 \mathrm{Mbps}, \ldots, 1.87 \mathrm{Mbps}, 2.0 \mathrm{Mbps}\}A:{0.7Mbps,0.83Mbps,…,1.87Mbps,2.0Mbps}
Reward:R ^ = α × ( t h r o u g h p u t − l o s s ) / d e l a y − β × ∣ q n − q n − 1 ∣ \hat{R}=\alpha \times( throughput - loss ) / delay -\beta \times\left|q_{n}-q_{n-1}\right|R^=α×(throughput−loss)/delay−β×∣qn−qn−1∣,α = 5 , β = 0.5 \alpha=5, \beta=0.5α=5,β=0.5
注意: 为了保证RL-based能充分地探索带宽,reward中的delay设置为链路中的min-delay。
2.4 双注意力机制融合(加权融合)
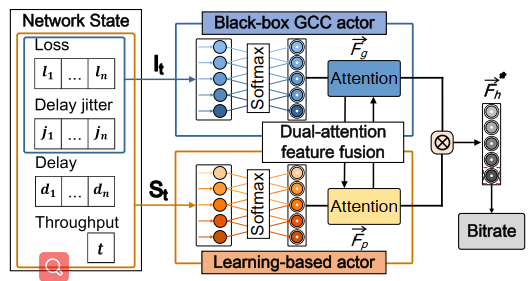
基于注意力的特征融合常用于整合不同层次的特征。
GCC actor输入:I t = ( l ⃗ t , j ⃗ t ) I_{t}=\left(\vec{l}_{t}, \vec{j}_{t}\right)It=(lt,jt)
GCC actor输出:F ⃗ g = [ g 1 , g 2 , … , g n ] \vec{F}_{g}=\left[g_{1}, g_{2}, \ldots, g_{n}\right]Fg=[g1,g2,…,gn]
RL actor输入:S t = ( l t , j ⃗ t , d ⃗ t , t t ) S_{t}=\left(l_{t}, \vec{j}_{t}, \vec{d}_{t}, t_{t}\right)St=(lt,jt,dt,tt)
RL actor输出:F ⃗ p = [ p 1 , p 2 , … , p n ] \vec{F}_{p}=\left[p_{1}, p_{2}, \ldots, p_{n}\right]Fp=[p1,p2,…,pn]
出发点:RL actor经常出现过估计,而GCC经常产生保守的比特率动作。另一方面,RL actor性能良好,当网络状况恢复时可以快速探索,优于GCC的慢恢复。
当怀疑网络带宽下降时,通过乘一个比例因子来扩大GCC的注意力权重;当网络带宽出现增长时,通过使用sigmoid函数来削弱权值。⊗ \otimes⊗表示元素乘法。
f ( F ⃗ g ) = { e β ∗ F ⃗ g , argmax ( F ⃗ g ) ≤ Γ Sigmoid ( F ⃗ g ) , else f\left(\vec{F}_{g}\right)= \begin{cases}e^{\beta * \vec{F}_{g}}, & \operatorname{argmax}\left(\vec{F}_{g}\right) \leq \Gamma \\ \operatorname{Sigmoid}\left(\vec{F}_{g}\right), & \text { else }\end{cases}f(Fg)=⎩⎨⎧eβ∗Fg,Sigmoid(Fg),argmax(Fg)≤Γ else
F → h ∗ = f ( F ⃗ g ) ⊗ F ⃗ p \overrightarrow{\mathbf{F}}_{\mathbf{h}}^{*}=f\left(\vec{F}_{g}\right) \otimes \vec{F}_{p}Fh∗=f(Fg)⊗Fp
Bitrate = A [ argmax ( F h → ∗ ) ] \text { Bitrate }=\mathcal{A}\left[\operatorname{argmax}\left(\overrightarrow{\mathbf{F}_{\mathbf{h}}}^{*}\right)\right] Bitrate =A[argmax(Fh∗)]
3. 性能评估与分析
3.1 与Baseline算法之间的对比
baseline - GCC、OnRL、Orca-plus
1)传输层参数
- Loki能够有效减少长尾效应的产生
- 在不同的网络下表现一致,鲁棒性好


2)应用层参数

- Loki在降低卡顿方面效果明显
- 证明了特征融合算法相较于时分复用算法的优越性
3)QoE
作者用用户观看时间的长短表征QoE。结果显示,Loki的用户观看市场均高于其他算法,证明了其在传输层和应用层的性能提升可以直接反应在QoE上。

3.2 GCC黑盒化验证
GCC转换为GCC actor后,仍保持与原有算法一致的行为和性能。


3.3 特征级融合效果验证
1)自身分析
- 当带宽增加时,如虚线框中所强调的,GCC产生了过于保守的码率估计,而RL-based actor则可以进行快速探索。
- 当带宽突然下降时,GCC乘性减小迅速降低其比特率,而RL-based actor仍然保持其高比特率估计一段时间。在这种情况下,Loki自动生成一个更接近GCC行为的比特率。

2)对比分析
- 平均融合
- 切换混合
- 早期特征混合
- Loki式混合
对不同方案的吞吐量、帧抖动和卡顿比例进行统计

4. Hybrid算法总结
| 算法 | Hybrid方式 | Hybrid类型 | 缺点 |
|---|---|---|---|
| Orca | 在粗粒度时间线上,RL以细粒度层面决策的CWND为基准对CWND进行调整 | 决策层面 | 传输层参数明显的长尾效应 |
| OnRL | RL表现不佳时切换至GCC | 决策层面 | 切换至GCC的时候拥塞已经出现,为时已晚 |
| HRCC | 在粗粒度时间线上,RL以细粒度层面决策的码率为基准对码率进行调整 | 决策层面 | 在时分复用的方案下,RL还不足以把GCC调整到比较好的水平 |
| Gemini | 对两类算法结果进行加权,然后输出 | 决策层面 | 简单加权不能确保算法真正学到了两类算法的优点 |
| Loki | 将启发式转换为NN,在特征层面进行深耦合 | 特征层面 |
5. 讨论与思考
作者讨论:
- 考虑结合其他启发式启发式算法
- 考虑将RL算法"白盒化",解释为rule-based的启发式算法。但这种方法的问题在于,1)转换过程难度大;2)转换后两个rule-based的算法只能做"决策级"的融合,无法像本文一样做"特征级"的融合
- 移动设备的在线训练
- 确实是做到了深度融合
- 作者在训练两个单独的actor的时候,都对其各自的特性进行了针对性的设计,以保证二者各自的优势。
- 双注意力机制特征之间点乘后是否再输入了一个网络?框图中有,内容中也提到融合过程需要训练,但文章没有对这个网络给出具体说明。
- 特征融合的时候,输入的GCC码率较上一次增益的概率分布,RL估计码率的概率分布。两者的不匹配会不会影响?
- 将GCC转换为NN后,GCC actor本身是否鲁棒?