逻辑回归的大致过程_R语言:逻辑回归ROC曲线对角线分析过程及结果 - lico9e

之前我们讨论了使用ROC曲线来描述分类器的优势，有人说它描述了“随机猜测类别的策略”，让我们回到ROC曲线来说明。考虑一个非常简单的数据集，其中包含10个观测值(不可线性分离)

在这里我们可以检查一下，确实是不可分离的

plot(x1,x2,col=c("red","blue")[1+y],pch=19) 

考虑逻辑回归

reg = glm(y~x1+x2,data=df,family=binomial(link = "logit"))

我们可以使用我们自己的roc函数

2. roc=function(s,print=FALSE){

3. Ps=(S<=s)*1

5. FP=sum((Ps==1)*(Y==0)/sum(Y==0)

7. TP=sum((Ps==1)*(Y==1)/sum(Y==1)

9. if(print==TRUE){

11. print(table(Observed=Y,Predicted=Ps))

14. vect=c(FP,TP)

16. names(vect)=c("FPR","TPR")

或R包

performance(prediction(S,Y),"tpr","fpr")

我们可以在这里同时绘制两个

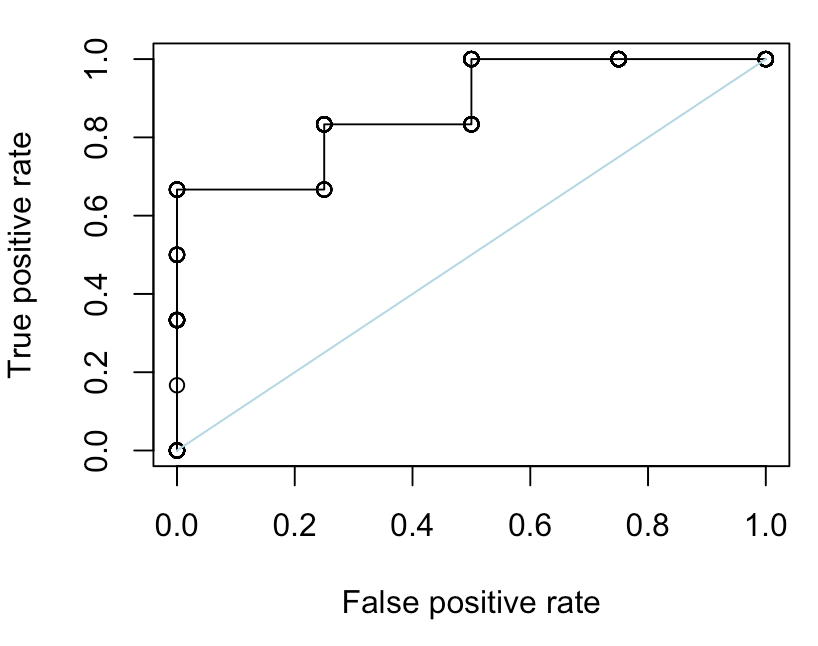
因此，我们的代码在这里可以正常工作。让我们考虑一下对角线。第一个是：每个人都有相同的概率(例如50％)

2. points(V[1,],V[2,])

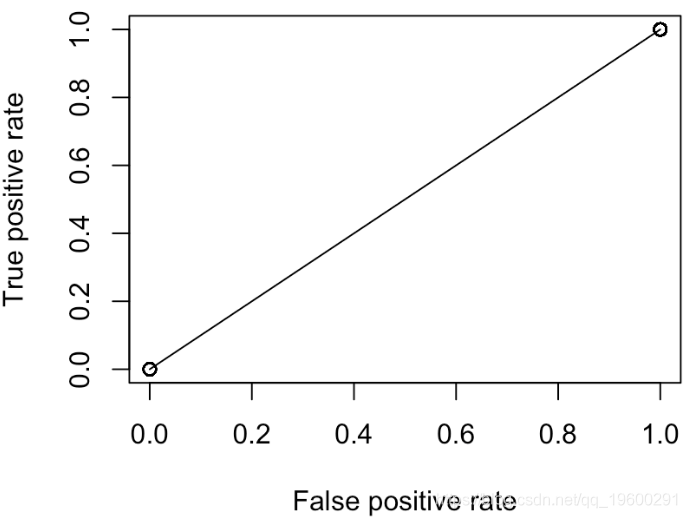
但是，我们这里只有两点：(0,0)和(1,1)。实际上，无论我们选择何种概率，都是这种情况

2. plot(performance(prediction(S,Y),"tpr","fpr"))

3. points(V[1,],V[2,])

我们可以尝试另一种策略，例如“通过扔无偏硬币进行预测”。我们得到

2. segments(0,0,1,1,col="light blue")

我们还可以尝试“随机分类器”，在其中我们随机选择分数

3. S=runif(10)

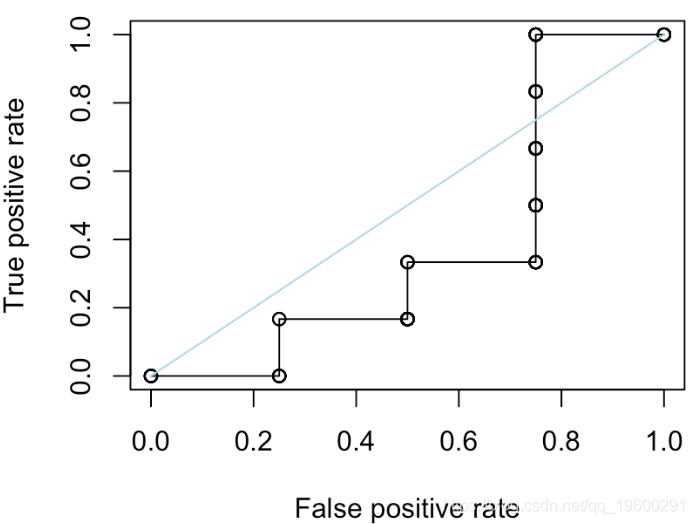
更进一步。我们考虑另一个函数来绘制ROC曲线

1. y=roc(x)

2. lines(x,y,type="s",col="red")

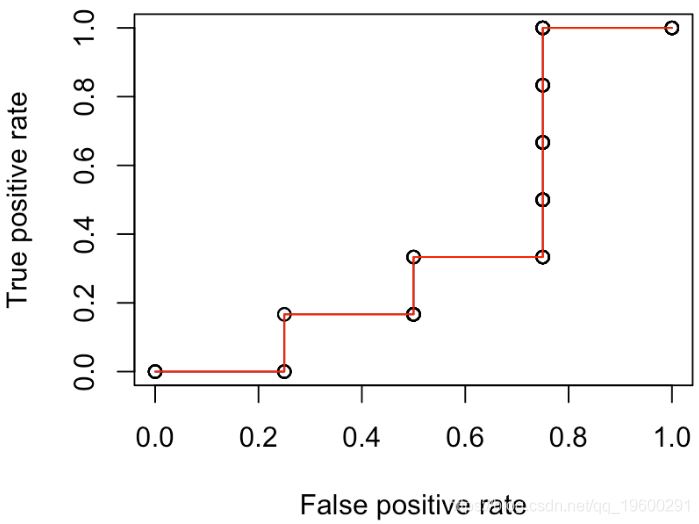
但是现在考虑随机选择的策略

2. for(i in 1:500){

3. S=runif(10)

4. V=Vectorize()(seq(0,1,length=251)

5. MY[i,]=roc_curve(x)

红线是所有随机分类器的平均值。它不是一条直线，我们观察到它在对角线周围的波动。

3. reg = glm(PRO~.,data=my,family=binomial(link = "logit"))

6. plot(performance(prediction(S,Y),"tpr","fpr"))

9. segments(0,0,1,1,col="light blue")

这是一个“随机分类器”，我们在单位区间上随机绘制分数

3. segments(0,0,1,1,col="light blue")

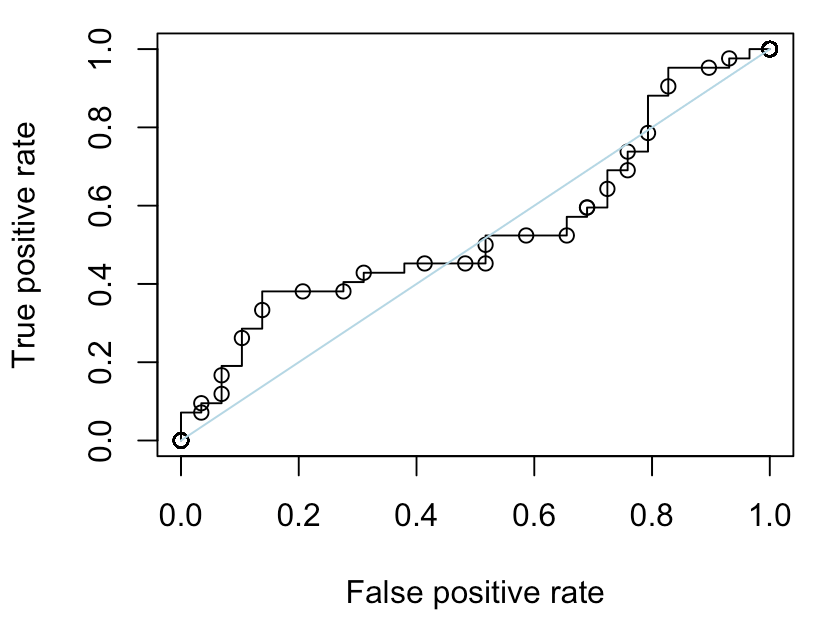
如果我们重复500次，我们可以获得

2. for(i in 1:500){

4. S=runif(length(Y))

7. MY[i,]=roc(x)

8. }

10. lines(c(0,x),c(0,apply(MY,2,mean)),col="red",type="s",lwd=3)

11. segments(0,0,1,1,col="light blue")

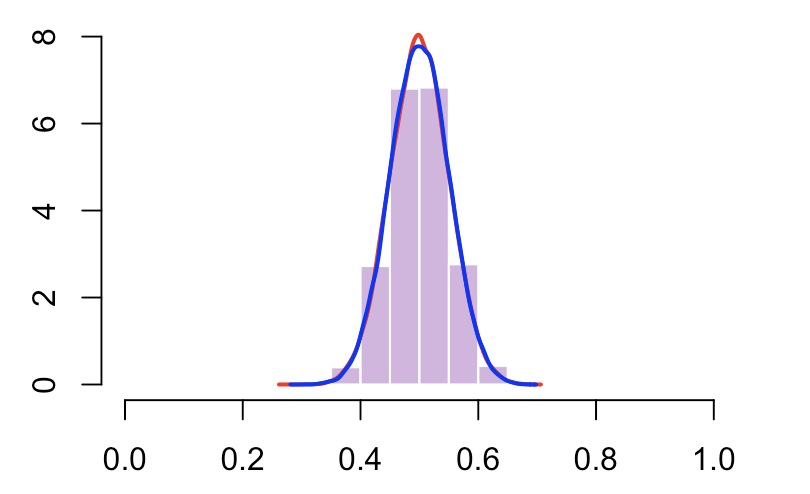
因此，当我在单位区间上随机绘制分数时，就会得到对角线的结果。给定Y，我们可以绘制分数的两个经验累积分布函数

3. plot(f0,(0:(length(f0)-1))/(length(f0)-1))

5. lines(f1,(0:(length(f1)-1))/(length(f1)-1))

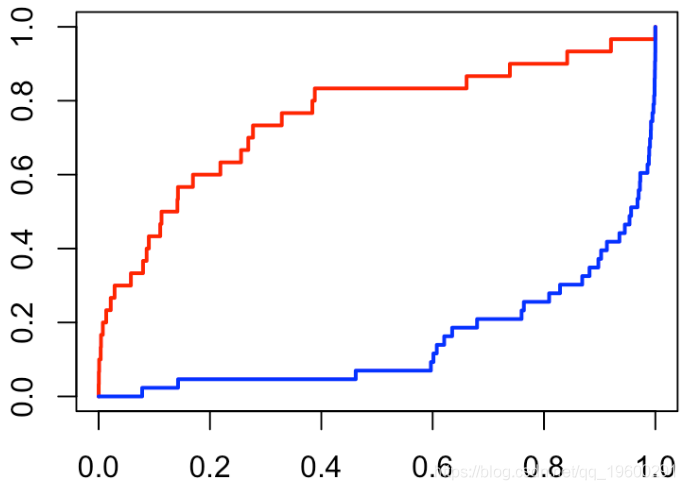
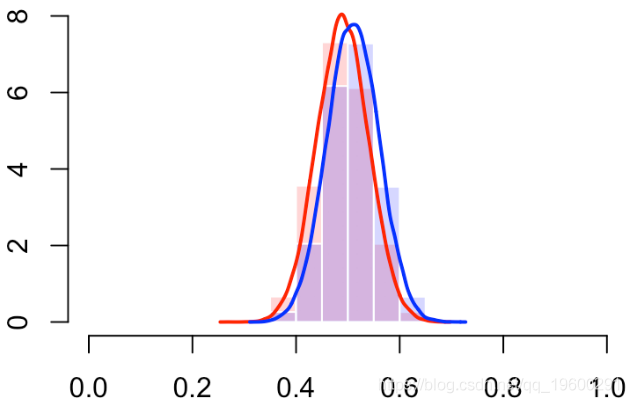
我们还可以使用直方图(或密度估计值)查看分数的分布

1. hist(S[Y==0],col=rgb(1,0,0,.2),

2. probability=TRUE,breaks=(0:10)/10,border="white")

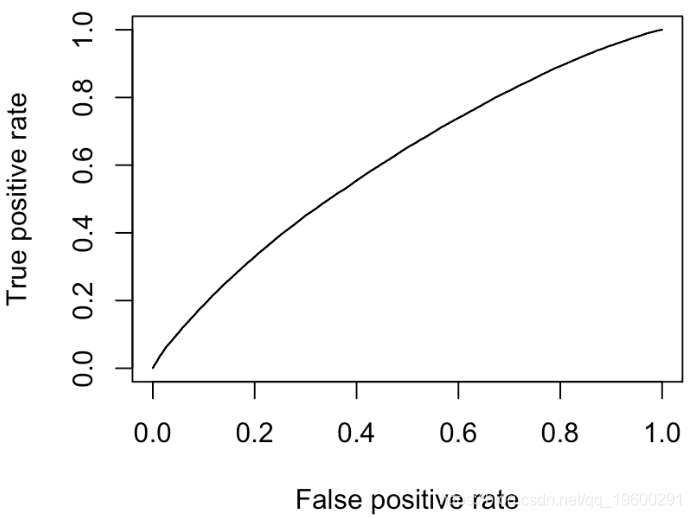
我们确实有一个“完美的分类器”(曲线靠近左上角)

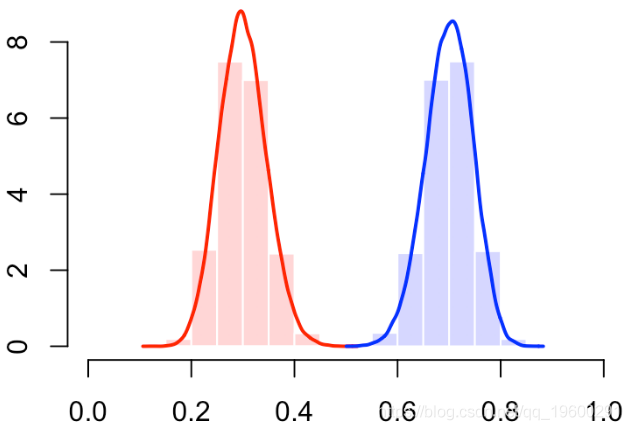
有错误。那应该是下面的情况

在10％的情况下，我们可能会分类错误

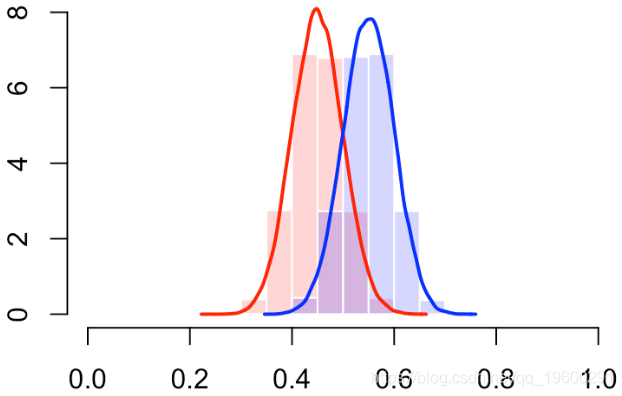
更多的错误分类

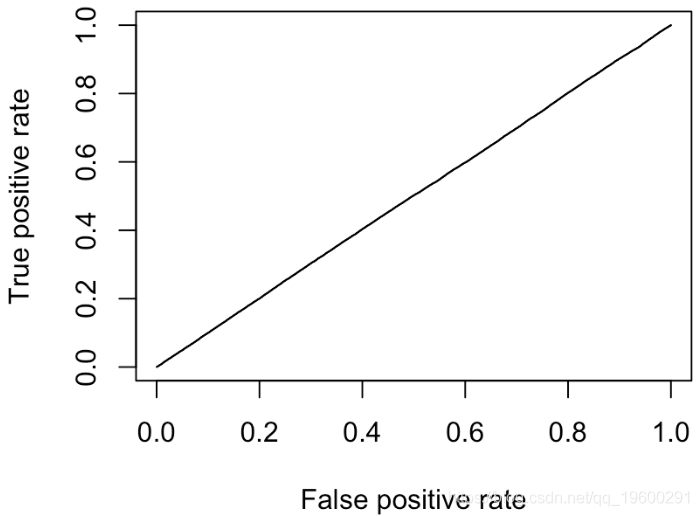
最终我们有对角线

最受欢迎的见解

语言多元Logistic逻辑回归 应用案例

2.面板平滑转移回归(PSTR)分析案例实现

中的偏最小二乘回归(PLSR)和主成分回归(PCR)

语言泊松Poisson回归模型分析案例

语言回归中的Hosmer-Lemeshow拟合优度检验

语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

用线性回归预测股票价格

语言如何在生存分析与Cox回归中计算IDI，NRI指标