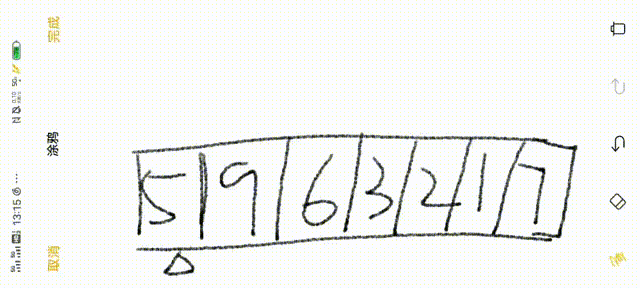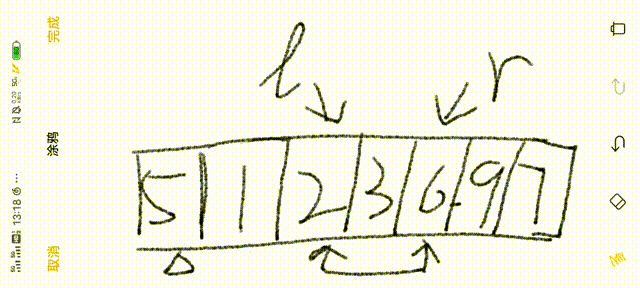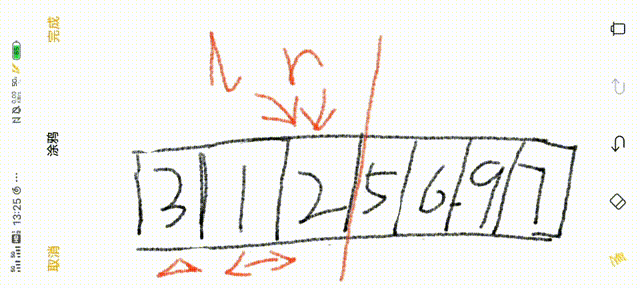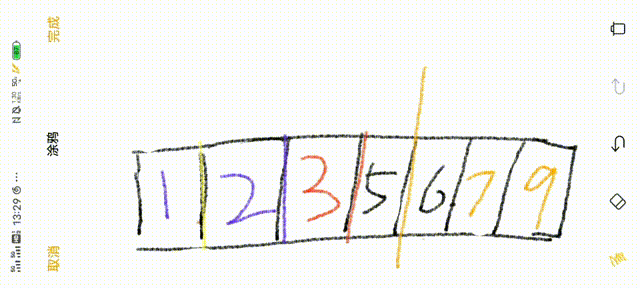
一、算法介绍

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。因其排序效率在同为O(N*logN)的几种排序方法中效率较高而受众人关注。

二、算法分析

时间复杂度：O(n2)
最优时间复杂度：O(n * logn)
平均时间复杂度：O(n * logn)
空间复杂度：根据实现的方式不同而不同
稳定性：不稳定

三、算法描述

1. 在序列中选择一个元素作为“基准点”（默认选择最左边的元素）
2. 将所有小于“基准点”的元素都移到左边，
   所有大于“基准点”的元素都移到右边,将最后一位较小的数与基准数互换
3. 对“基准点”左边和右边的两个子序列，不断重复步骤 1 和 2

四、算法步骤(简单理解)

自制动态图

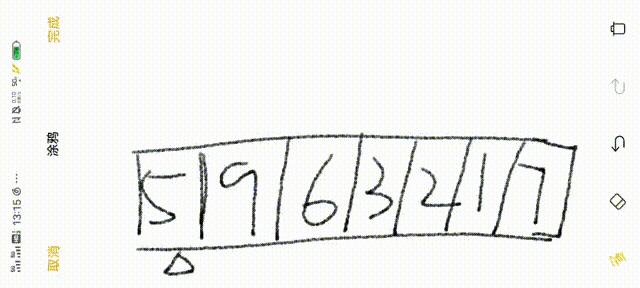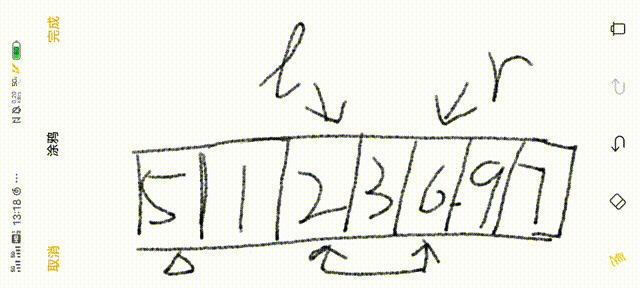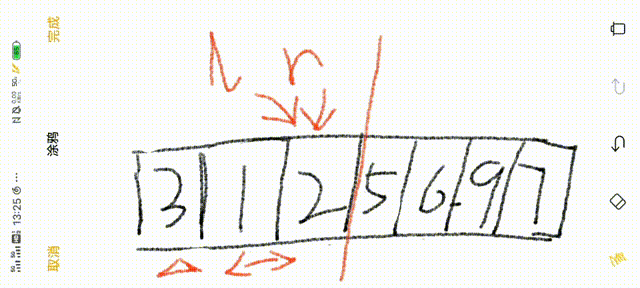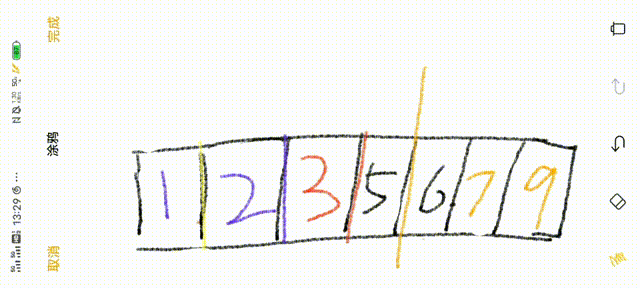
首先我们假定一个整型数组 a[7]={5,9,6,3,2,1,7}，我们对它进行快速排序操作

1.先选择最左边的数为基准数（三角下标所指的）

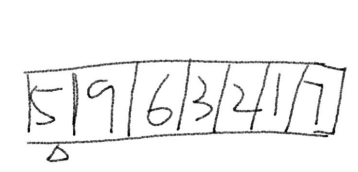
2.接下来令left、right分别指向最左边和最右边的数值（l与r）

3.r从右往左，找到比基准数小的数值

4.l从左往右，找到比基准数大的数值

5.交换两值

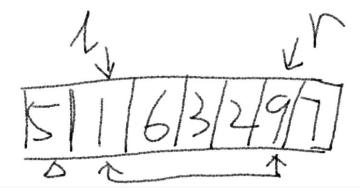
6.r继续向左前进，重复3-5步

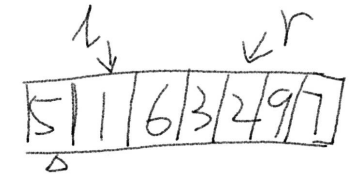
7.当r与l同时指向一个数值时，将基准数与该数值交换

8.分成左右两个子序列，重复1-8步

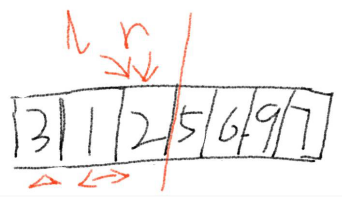
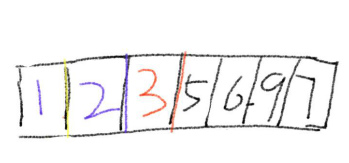
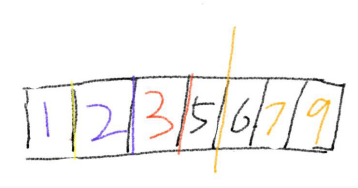
9.至此为止，快速排序已完成

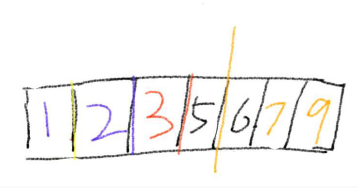
五、主体代码

以下是c语言实现的主体代码

#include <stdio.h>

void sort3(int array[], int low, int high);
void swap(int array[], int low, int high);

int main() {
    int array[6] = {0};
    int length = sizeof(array)/sizeof(array[0]);

    printf("请输入六个数字:");
    for (int i = 0; i < length; i++) {
        //输入六个数字
        scanf_s("%d",&array[i]);
    }
    printf("\n排序前：");
    for (int i = 0; i < length; i++) {
        printf("%d ", array[i]);
    }
    
    sort3(array, 0, length - 1);
    
    printf("\n排序后：");
    for (int i = 0; i < length; i++) {
        printf("%d ", array[i]);
    }

    return 0;
}

/*
* 交换两数
* */
void swap(int array[], int i, int j) {
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

/*
* 快排主体
* */
void sort3(int array[], int low, int high) {

    int i = low;
    int j = high;
    
    if(array == null || i >= j){
        return;
    }
    
    int povit = array[low];

    while (i < j) {

        //从右往左查找比基准povit还小的值的下标
        while (i < j && povit <= array[j]) {
            j--;
        }

        //从右往左查找比基准povit还小的值的下标
        while (i < j && povit >= array[i]) {
            i++;
        }

        //将二者交换位置
        if (i < j) {
            swap(array, i, j);
        }

    }
    //将基准数放在中间
    array[low] = array[i];
    array[i] = povit;

    //利用递归处理左右两边的子序列
    sort3(array, low, i - 1);
    sort3(array, i + 1, high);
}

以下是java实现的主体代码：

参考：快速排序（Quick Sort）

package com.makonike.java2;

/**
 * @author Makonike
 * @date 2021-03-23 23:15
 **/
public class QuickSort {

    public static void quickSort(int[] array){
        if(array!=null){
            //传入最左边的数值下标和最右边的数值下标，先进行初次排序
            quickSort(array,0,array.length - 1);
        }
    }

    public static void quickSort(int[] array,int low, int high) {
        if(array == null || low >= high || array.length == 1){
            return;
        }
        int mid = partition(array,low,high);
        //对左边的子序列通过递归排序
        quickSort(array,low,mid - 1);
        //对右边的子序列通过递归排序
        quickSort(array,low + 1,high);
    }

    public static int partition(int[] array,int low, int high) {
        //取得默认基准数为最左边的数值
        int index = array[low];
        //主体代码
        while( low < high ){
            //从右往左查找比基准数小的值的下标
            while(low < high && index <= array[high]){
                high--;
            }
            //将找到的值填到最左边的数值
            if(low < high){
                array[low] = array[high];
            }
            //从右往左查找比基准数小的值
            while(low < high && index >= array[low]){
                low++;
            }
            //将找到的值填到右边找到的数值
            if(low < high){
                array[high] = array[low];
            }

        }
        //将基准数填到中间
        array[low] = index;
        return low;
    }

}

package com.makonike.java2;

import static com.makonike.java2.QuickSort.quickSort;

/**
 * @author Makonike
 * @date 2021-03-23 23:42
 **/
public class QuickSortTest {

    public static void main(String[] args) {
        int[] a = {5,9,6,3,2,1,7 };
        for (int i : a) {
            System.out.print(i + " ");
        }
        System.out.println();
        quickSort(a);
        for (int i : a) {
            System.out.print(i + " ");
        }
    }

}

拓展

为什么快速排序要先从右边开始
快速排序法为什么一定要从右边开始的原因
挖坑与分治
白话经典算法系列之六 快速排序 快速搞定