详解小波变换在图像分解中的应用

参考链接

# pywt.threshold方法讲解： 
#        pywt.threshold（data，value，mode ='soft'，substitute = 0 ） 
#        data：数据集，value：阈值，mode：比较模式默认soft，substitute：替代值，默认0，float类型 
 
#data:  [ 1.  1.5 2.  2.5 3.  3.5 4. ] 
#output：[ 6.  6.  0.  0.5 1.  1.5 2. ] 
#soft 因为data中1小于2，所以使用6替换，因为data中第二个1.5小于2也被替换，2不小于2所以使用当前值减去2，，2.5大于2，所以2.5-2=0.5..... 

小波，一个神奇的波，可长可短可胖可瘦（伸缩平移），当去学习小波的时候，第一个首先要做的就是回顾傅立叶变换（又回来了，唉），因为他们都是频率变换的方法，而傅立叶变换是最入门的，也是最先了解的，通过傅立叶变换，了解缺点，改进，慢慢的就成了小波变换。

主要的关键的方向是傅立叶变换、短时傅立叶变换，小波变换等。

当然，其中会看到很多的名词，例如，内积，基，归一化正交，投影，Hilbert空间，多分辨率，父小波，母小波，这些不同的名词也是学习小波路上的标志牌，所以在刚学习小波变换的时候，看着三个方向和标志牌，可以顺利的走下去。

一、基

对于傅立叶变换的基是不同频率的正弦曲线，所以傅立叶变换是把信号波分解成不同频率的正弦波的叠加和，而对于小波变换就是把一个信号分解成一系列的小波，

这里时候，也许就会问，小波变换的小波是什么啊，

定义中就是告诉我们小波，因为这个小波实在是太多，一个是种类多，还有就是同一种小波还可以尺度变换，但是小波在整个时间范围的幅度平均值是 0，具有有限的持续时间和突变的频率和振幅，

可以是不规则，也可以是不对称,很明显正弦波就不是小波，什么的是呢，看下面几个图就是

下面看一个傅立叶变换的实例：

对于一个信号的表达式为：$x=sin(2\ast pi\ast t)+0.5\ast sin(2\ast pi\ast 5\ast t)$;

这里可以看到是他的基就是 sin 函数，频率是 1 和 5，下面看看图形的表示，是不是感受到了频域变换给人的一目了然。

二、内积

三、短时傅立叶变换（Short-time Fourier Transform,STFT）

四、小波变换

4.1 wavefun()
wavefun()方法可以在给定的分解阶次上依据小波系数近似给出尺度函数（phi）和小波函数（psi）。

对于正交小波：

>>> import pywt
>>> wavelet = pywt.Wavelet('db2')
>>> phi, psi = wavelet.wavefun(level=5)

五、小波的深入

六、小波变换库

本文介绍了Python小波分析库Pywavelets，分享给大家，具体如下：

# -*- coding: utf-8 -*- 
import numpy as np
import math
import matplotlib.pyplot as plt
import pandas as pd
import datetime 
from scipy import interpolate
from pandas import DataFrame,Series

import numpy as np 
import pywt 

data = np.linspace(1, 4, 7) 
# pywt.threshold方法讲解： 
#        pywt.threshold（data，value，mode ='soft'，substitute = 0 ） 
#        data：数据集，value：阈值，mode：比较模式默认soft，substitute：替代值，默认0，float类型 

#data:  [ 1.  1.5 2.  2.5 3.  3.5 4. ] 
#output：[ 6.  6.  0.  0.5 1.  1.5 2. ] 
#soft 因为data中1小于2，所以使用6替换，因为data中第二个1.5小于2也被替换，2不小于2所以使用当前值减去2，，2.5大于2，所以2.5-2=0.5..... 

print(pywt.threshold(data, 2, 'soft',6))  

#data:  [ 1.  1.5 2.  2.5 3.  3.5 4. ] 
#hard data中绝对值小于阈值2的替换为6，大于2的不替换 
print (pywt.threshold(data, 2, 'hard',6)) 

#data:  [ 1.  1.5 2.  2.5 3.  3.5 4. ] 
#data中数值小于阈值的替换为6，大于等于的不替换 
print (pywt.threshold(data, 2, 'greater',6) )

print (data )
#data:  [ 1.  1.5 2.  2.5 3.  3.5 4. ] 
#data中数值大于阈值的，替换为6 
print (pywt.threshold(data, 2, 'less',6) )

[6. 6. 0. 0.5 1. 1.5 2. ]
[6. 6. 2. 2.5 3. 3.5 4. ]
[6. 6. 2. 2.5 3. 3.5 4. ]
[1. 1.5 2. 2.5 3. 3.5 4. ]
[1. 1.5 2. 6. 6. 6. 6. ]

#!/usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt

import pywt
import pywt.data


ecg = pywt.data.ecg()

data1 = np.concatenate((np.arange(1, 400),
            np.arange(398, 600),
            np.arange(601, 1024)))
x = np.linspace(0.082, 2.128, num=1024)[::-1]
data2 = np.sin(40 * np.log(x)) * np.sign((np.log(x)))

mode = pywt.Modes.smooth


def plot_signal_decomp(data, w, title):
  """Decompose and plot a signal S.
  S = An + Dn + Dn-1 + ... + D1
  """
  w = pywt.Wavelet(w)#选取小波函数
  a = data
  ca = []#近似分量
  cd = []#细节分量
  for i in range(5):
    (a, d) = pywt.dwt(a, w, mode)#进行5阶离散小波变换
    ca.append(a)
    cd.append(d)

  rec_a = []
  rec_d = []

  for i, coeff in enumerate(ca):
    coeff_list = [coeff, None] + [None] * i
    rec_a.append(pywt.waverec(coeff_list, w))#重构

  for i, coeff in enumerate(cd):
    coeff_list = [None, coeff] + [None] * i
    if i ==3:
      print(len(coeff))
      print(len(coeff_list))
    rec_d.append(pywt.waverec(coeff_list, w))

  fig = plt.figure()
  ax_main = fig.add_subplot(len(rec_a) + 1, 1, 1)
  ax_main.set_title(title)
  ax_main.plot(data)
  ax_main.set_xlim(0, len(data) - 1)

  for i, y in enumerate(rec_a):
    ax = fig.add_subplot(len(rec_a) + 1, 2, 3 + i * 2)
    ax.plot(y, 'r')
    ax.set_xlim(0, len(y) - 1)
    ax.set_ylabel("A%d" % (i + 1))

  for i, y in enumerate(rec_d):
    ax = fig.add_subplot(len(rec_d) + 1, 2, 4 + i * 2)
    ax.plot(y, 'g')
    ax.set_xlim(0, len(y) - 1)
    ax.set_ylabel("D%d" % (i + 1))


#plot_signal_decomp(data1, 'coif5', "DWT: Signal irregularity")
#plot_signal_decomp(data2, 'sym5',
#          "DWT: Frequency and phase change - Symmlets5")
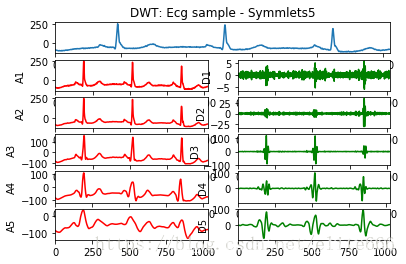
plot_signal_decomp(ecg, 'sym5', "DWT: Ecg sample - Symmlets5")


plt.show()

72
5

七、db1,db2,db3小波不同之处

参考链接

db小波是小波家族的一部分，专业地称它们为多贝西极限相位小波。

db后面那个数字代表的是消失矩，一般来说，这个消失矩的数字越大，这个小波越光滑（长的小波滤波器），小波滤波器的长度（尺度）是这个数字的两倍。

消失矩为N的小波正交于最多N阶多项式。因此，如果一个多项式信号的阶数最高是1的话，在一个区间上一个‘db1’小波的小波系数是0

[LoD,HiD] = wfilters(‘db2’); %db2小波滤波器
length(LoD) %answer is 4=22 %结果长度为4
[LoD,HiD] = wfilters(‘db3’); %db3小波滤波器
length(LoD) %answer is 6=23 %结果长度为6

因此，如果一个多项式信号的阶数最高是1的话，在一个区间上一个‘db1’小波的小波系数是0。
例如

t = linspace(0,1,512);
dwtmode(‘per’);
y = t+1; % polynomial of degree 1
[C1,L1] = wavedec(y,2,‘db1’);
d1 = detcoef(C1,L1,1);
plot(d1) %detail coefficients are all approximately zero
y1 = t.^2+1; % polynomial of degree 2
[C2,L2] = wavedec(y1,2,‘db1’);
d1 = detcoef(C2,L2,1);
plot(d1) % detail coefficients are not all zero