子集问题1：

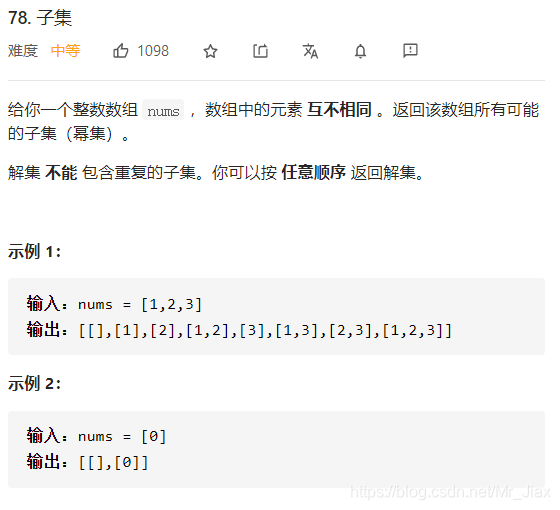
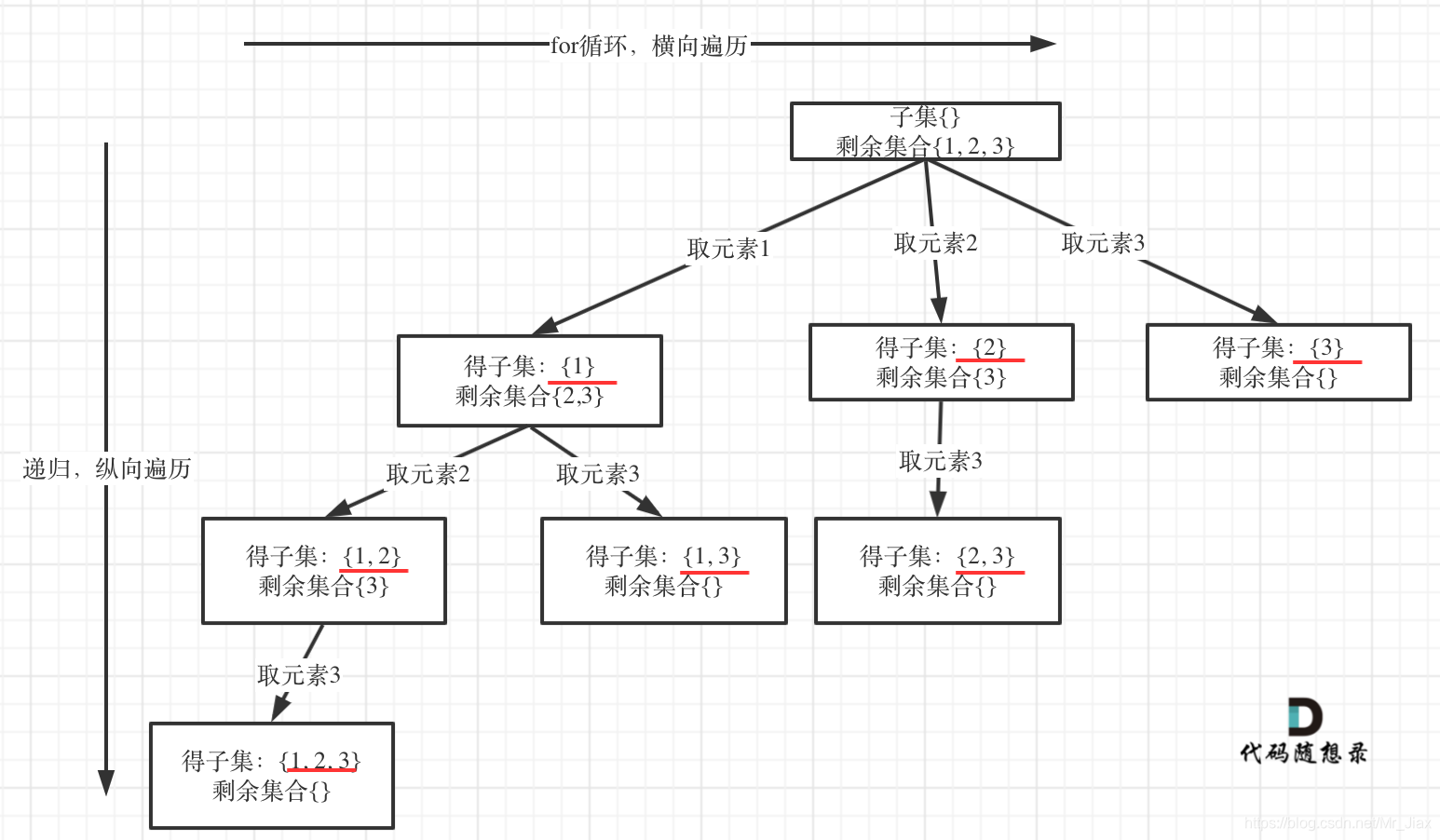
利用回溯法求解子集问题，可以将子集比作n叉树，由于该题中数组元素都不相等，则不需要进行去重

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> list=new ArrayList<>();
        backtrack(list,new ArrayList<>(),nums,0);
        return list;
    }

    public void backtrack(List<List<Integer>> list,List<Integer> templist,int[] nums,int start){
        list.add(new ArrayList<>(templist));
        if(start>=nums.length){
            return;
        }
        for(int i=start;i<nums.length;i++){

            templist.add(nums[i]);
            //递归
            backtrack(list,templist,nums,i+1);
            //撤销
            templist.remove(templist.size()-1);
        }
    }
}

子集问题2

由于该题数组中含有相同的元素，且解集中不能有重复的子集，因此需要用到去重，将子集问题抽象为树形结构时，去重包含两个维度，一个是同一树枝上不同有重复，还是同一层上不能有重复。本题是同一层上不能有重复。

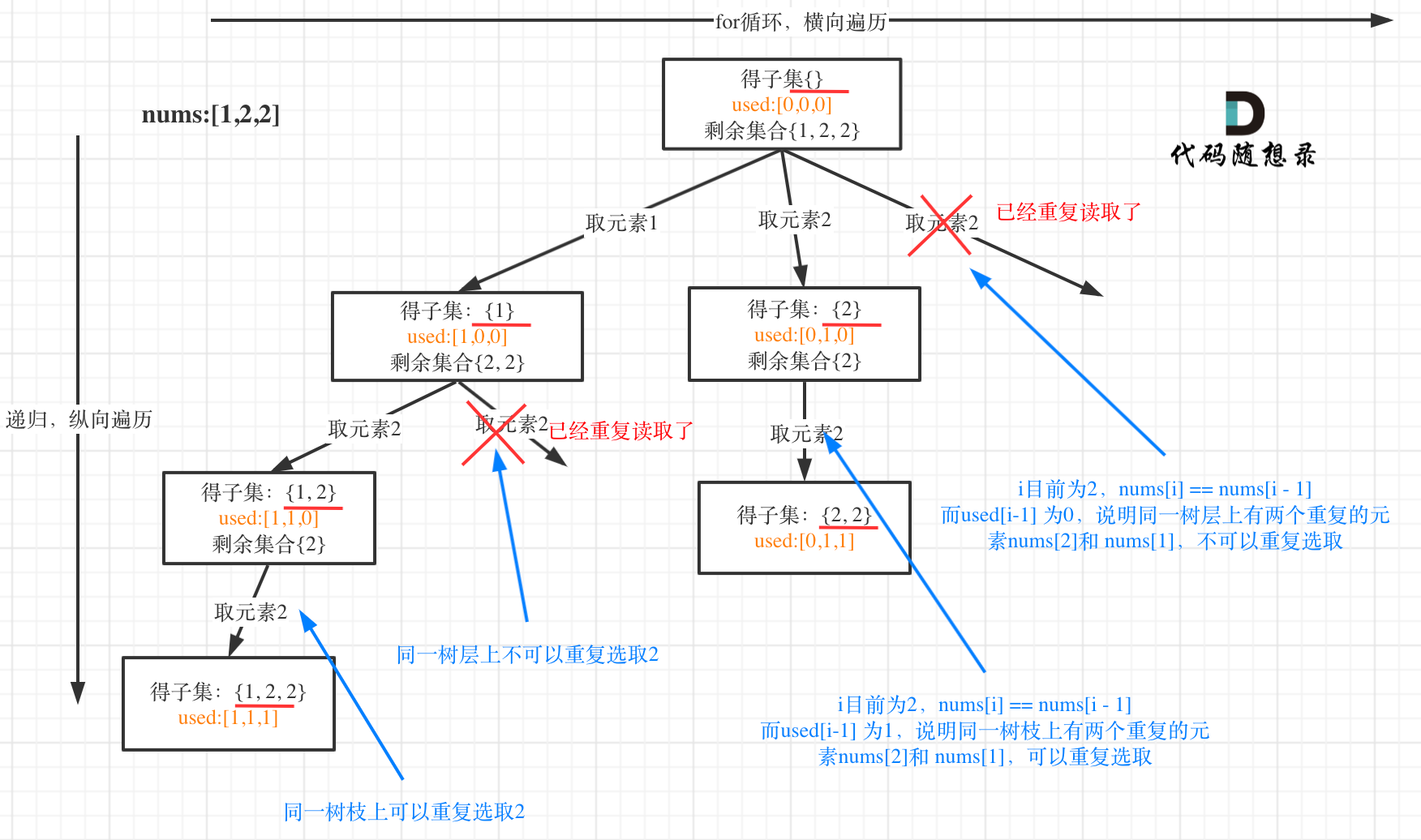
解题思路：首先对数组进行排序，去重代码，

if(i>start && nums[i]==nums[i-1]){
                continue;
 }

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        Arrays.sort(nums);
        backtrack(res,new ArrayList<>(),nums,0);
        return res;
    }
    public void backtrack(List<List<Integer>> list,List<Integer> templist,int[] nums,int start){
        list.add(new ArrayList<>(templist));
        for(int i=start;i<nums.length;i++){
            //去重
            if(i>start && nums[i]==nums[i-1]){
                continue;
            }
            templist.add(nums[i]);

            backtrack(list,templist,nums,i+1);

            templist.remove(templist.size()-1);
        }
    }
}