算法笔记——SBT – 源码巴士

SBT(Size Balanced Tree节点大小平衡树)是一种自平衡二叉查找树，通过子树的大小来保持平衡。与红黑树、AVL树等平衡二叉查找树相比，SBT更容易实现。SBT可以在 $O(logn)$ 的时间内完成所有二叉搜索树的相关操作，与普通二叉搜索树相比，SBT仅加入了简洁的核心操作maintain。由于SBT把持平衡的是size域而不是其他的域，所以可以方便地实现动态顺序统计中的第k小和排名操作。

SBT性质

对SBT的每个节点T，其左儿子为L，右儿子为R，子树A、B为L的左右子树，C、D为R的左右子树。T右子树的大小都大于等于T左子树的两个子树的大小，即 $size[R]\geqslant size[A],size[R]\geqslant size[B]$ ；T左子树的大小都大于等于右子树的两个子树的大小，即 $size[L]\geqslant size[C],size[L]\geqslant size[D]$ 。也就是说，“叔叔”≥“侄子”

1、左旋和右旋

void R_rotate(int &x)
{
    int y=tr[x].ls;
    tr[x].ls=tr[y].rs;
    tr[y].rs=x;
    tr[y].size=tr[x].size;
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
    x=y;
}

void L_rotate(int &x)
{
    int y=tr[x].rs;
    tr[x].rs=tr[y].ls;
    tr[y].ls=x;
    tr[y].size=tr[x].size;
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
    x=y;
}

2、维护

插入新节点时，有可能不满足SBT的性质，需要根据插入位置的不同，进行相应的旋转，以达到平衡状态。调整平衡分为4种情况：LL、LR、RR和RL。

（1）LL型。一棵SBT，若将新节点x插入节点A（T左子树的左子树）之后，节点T出现了不平衡（ $size[A]\geqslant size[R]$ ），则属于LL型不平衡，需要将节点T右旋。

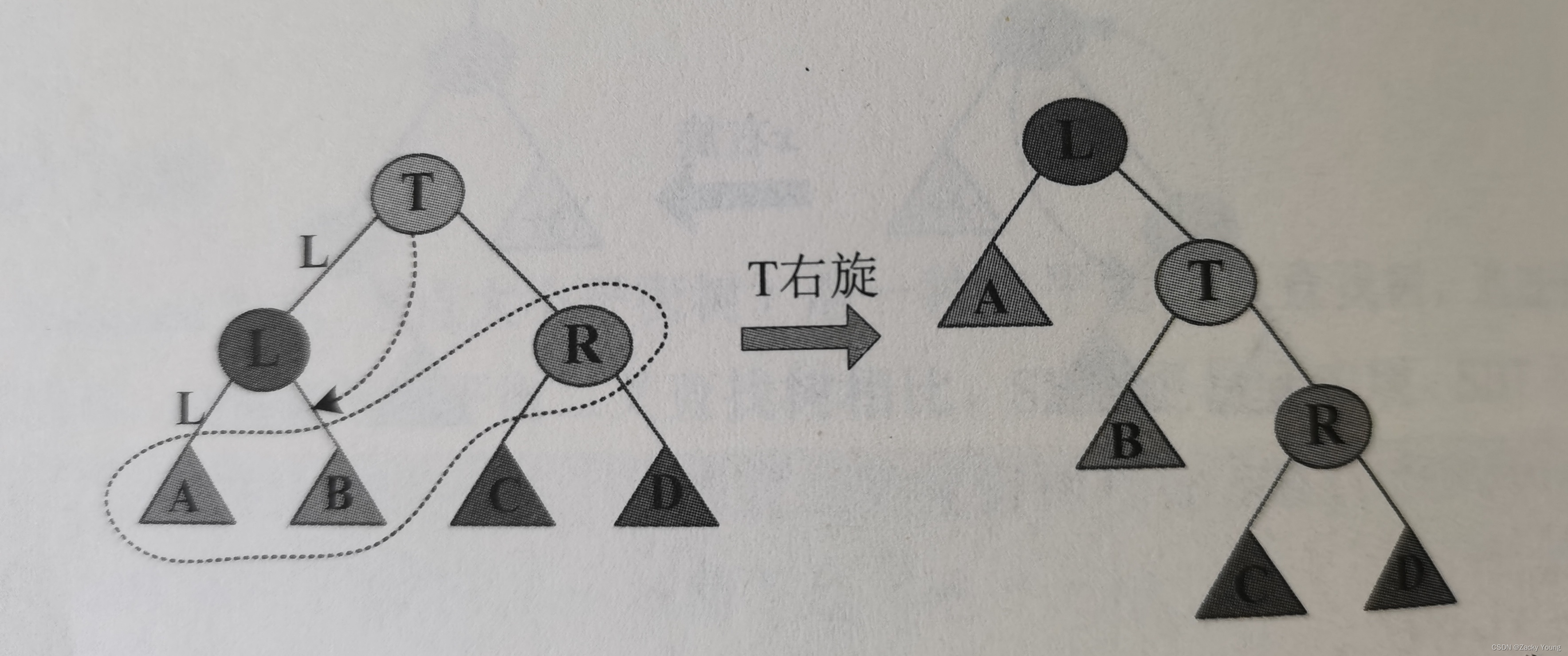
旋转之后，A、B和R仍是SBT。L的右子树T可能会出现 $size[C]>size[B]$ 或 $size[D]>size[B]$ 的情况，即RL、RR型不平衡。因为 $size[B]\leqslant size[R]$ ，所以不会出现B的子树比R大的情况，即T不会出现LR、LL型不平衡。因此L的右子树只需向右判断两种不平衡RL、RR即可。旋转后，L自身也可能出现不平衡，需要继续调整平衡。

（2）LR型。有一棵SBT，若新节点x插入节点B（T左子树的右子树）之后，节点T出现了不平衡( $size[B]>size[R]$ ),则属于LR型不平衡，需要先将节点L左旋，然后将节点T右旋。

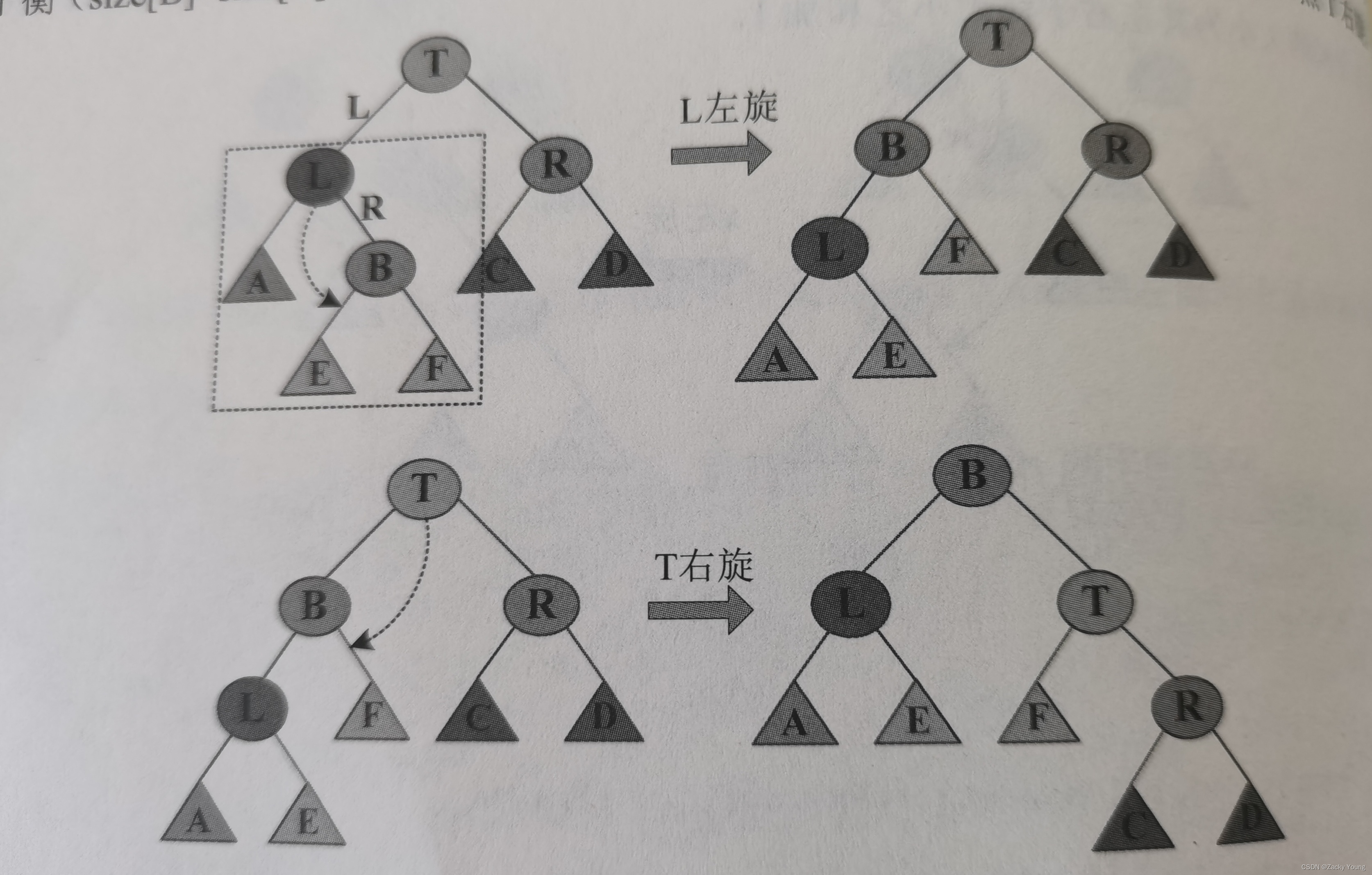
两次旋转之后，A、E、F和R仍是SBT。B的右子树T可能会出现 $size[C]>size[F]$ 或 $size[D]>size[F]$ ，即RL、RR型不平衡。B的左子树L， $size[E]\leqslant size[A]$ ，因此B的左子树只需想做判断两种不平衡LR、LL即可。

（3）RR型，与LL型对称。

（4）RL型，与LR型对称。

总结：

LL型，右旋T，L成为根，从T向右判断RL、RR不平衡。

LR型，左旋L，右旋T，B成为根，树根左子树向左判断LR、LL，右子树向右判断RL、RR。

RR型。左旋T，R成为根，从T向左判断LL、LR不平衡。

RL型，右旋R，左旋T，C成为根，树根左子树向左判断LR、LL，右子树向右判断RL、RR

void maintain(int &p,bool flag)//flag=false,向左,flag=true,向右
{
    if(!p) return;
    if(!flag)
    {
        if(tr[tr[tr[p].ls].ls].size>tr[tr[p].rs].size)//LL
            R_rotate(p);
        else if(tr[tr[tr[p].ls].rs].size>tr[tr[p].rs].size)//LR
            L_rotate(tr[p].ls),R_rotate(p);
        else return;
    }
    else
    {
        if(tr[tr[tr[p].rs].rs].size>tr[tr[p].ls].size)//RR
            L_rotate(p);
        else if(tr[tr[tr[p].rs].ls].size>tr[tr[p].ls].size)//RL
            R_rotate(tr[p].rs),L_rotate(p);
        else return;
    }
    maintain(tr[p].ls,false);
    maintain(tr[p].rs,true);
    maintain(p,false);
    maintain(p,true);
}

3、基本操作

（1）插入

从树根开始，若当前节点为空，则创建一个新节点，否则当前节点的大小加1，若待插入元素val小于当前节点的值，则插入当前节点的左子树，否则插入当前节点的右子树，然后根据插入子树的不同进行维护。

void insert(int &p,int val)
{
    if(!p)
    {
        p=++cnt;
        tr[p].ls=tr[p].rs=0;
        tr[p].size=1;
        tr[p].val=val;
    }
    else
    {
        tr[p].size++;
        if(val<tr[p].val) insert(tr[p].ls,val);
        else insert(tr[p].rs,val);
        maintain(p,val>=tr[p].val);
    }
}

（2）删除

删除操作和二叉搜索树的删除方法相同。删除之后，虽然不能保证这棵树是SBT，但是整棵树的最大深度并没有变化，所以时间复杂度不会增加。这是，maintain操作显得多余，因此删除操作没有调整平衡。

void remove(int &p,int val)
{
    if(!p) return;
    tr[p].size--;
    if(tr[p].val==val)
    {
        if(!tr[p].ls || !tr[p].rs)
            p=tr[p].ls+tr[p].rs;
        else
        {
            int temp=tr[p].rs;
            while(tr[temp].ls) temp=tr[temp].ls;
            tr[p].val=tr[temp].val;
            remove(tr[p].rs,tr[temp].val);  
        }
    }
    else if(val<tr[p].val) remove(tr[p].ls,val);
    else remove(tr[p].rs,val);
}

（3）查找

查找操作和二叉搜索树的查找方法一样，从树根开始，若当前节点为空或待查找元素val等于当前节点的值，则返回当前节点；若val小于当前节点的值，则到当前节点的左子树中查找，否则到当前节点的右子树中查找。

int find_v(int p,int val)
{
    if(!p || tr[p].val==val) return p;
    if(val<tr[p].val) return find_v(tr[p].ls,val);
    else return find_v(tr[p].rs,val);
}

（4）最小值

SBT是一棵二叉搜索树，满足中序有序性，因此从根开始一直向左，找到的最左节点就是最小节点。

int get_min()
{
    int p=root;
    while(tr[p].ls) p=tr[p].ls;
    return tr[p].val;
}

（5）最大值

从根开始找到的最右节点就是最大值。

int get_max()
{
    int p=root;
    while(tr[p].rs) p=tr[p].rs;
    return tr[p].val;
}

（6）前驱

val的前驱指二叉搜索树中第一个小于val的值。

求val的前驱，从跟开始，用p记录当前节点，用q记录查找路径上的前一个节点。若val大于当前节点的值，则到右子树中搜索，否则到左子树中搜索，当p为空时返回q节点的值，即为val的前驱。

int get_pre(int &p,int q,int val)
{
    if(!p) return tr[q].val;
    if(tr[p].val<val)
        return get_pre(tr[p].rs,p,val);
    else return get_pre(tr[p].ls,q,val);//要保证tr[q].val<val
}

（7）后继

int get_next(int &p,int q,int val)
{    
    if(!p) return tr[q].val;
    if(tr[p].val>val)
        return get_next(tr[p].ls,p,val);
    else return get_next(tr[p].rs,q,val);
}

（8）排名

求val的排名，从根开始，若val小于当前节点的值，则返回在左子树中的排名；若val大于当前节点的值，则返回在右子树中的排名+左子树的大小+1,；若val等于当前节点的值，则返回左子树的大小+1。

int get_rank(int &p,int val)
{
    if(val<tr[p].val)
        return get_rank(tr[p].ls,val);
    else if(val>tr[p].val)
        return get_rank(tr[p].rs,val)+tr[tr[p].ls].size+1;
    else return tr[tr[p].ls].size+1;
}

（9）第k小

从根开始，用s记录左子树的大小+1，若s等于k，则返回当前节点的值；若s小于k，则到右子树中查找第k-s个节点，否则到左子树中查找第k个节点。

int get_kth(int &p,int k)
{
    int s=tr[tr[p].ls].size+1;
    if(s==k)    return tr[p].val;
    if(s<k)    return get_kth(tr[p].rs,k-s);
    else return get_kth(tr[p].ls,k);
}

原文链接：https://blog.csdn.net/m0_67142204/article/details/126525100