
NO.04
ZEYI
04.2020
正文共: 3292字 52图 预计阅读时间: 9分钟 嘿喽,我是则已。这是stata的第四期学习。 前面学习了相关分析、主成分分析与因子分析。今天来学习:聚类分析、ols回归分析。 划线部分是自己要研究的变量。 聚类分析
前面学习了相关分析、主成分分析与因子分析。今天来学习:聚类分析、ols回归分析。 划线部分是自己要研究的变量。 聚类分析 聚类分析研究的是事物分类的基本方法,基于所研究的数据之间存在着不同程度的相似性来进行分析。主要有划分聚类法和层次聚类法。 01 划分聚类法 简划分聚类法是将样本数据划分到一系列事先设定好的不重合的分组去。划分聚类方法有两种:K个平均数的聚类分析法、K个中位数的聚类分析法。
聚类分析研究的是事物分类的基本方法,基于所研究的数据之间存在着不同程度的相似性来进行分析。主要有划分聚类法和层次聚类法。 01 划分聚类法 简划分聚类法是将样本数据划分到一系列事先设定好的不重合的分组去。划分聚类方法有两种:K个平均数的聚类分析法、K个中位数的聚类分析法。
 结果分析:可以看到均值基本上为0,标准差为1,说明标准化起到了一定效果。 进行K个平均数的聚类分析,并且分为两类:cluster kmeans zv2 zv3 zv4,k(2)
结果分析:可以看到均值基本上为0,标准差为1,说明标准化起到了一定效果。 进行K个平均数的聚类分析,并且分为两类:cluster kmeans zv2 zv3 zv4,k(2)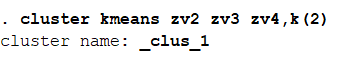 打开上方的数据浏览界面:
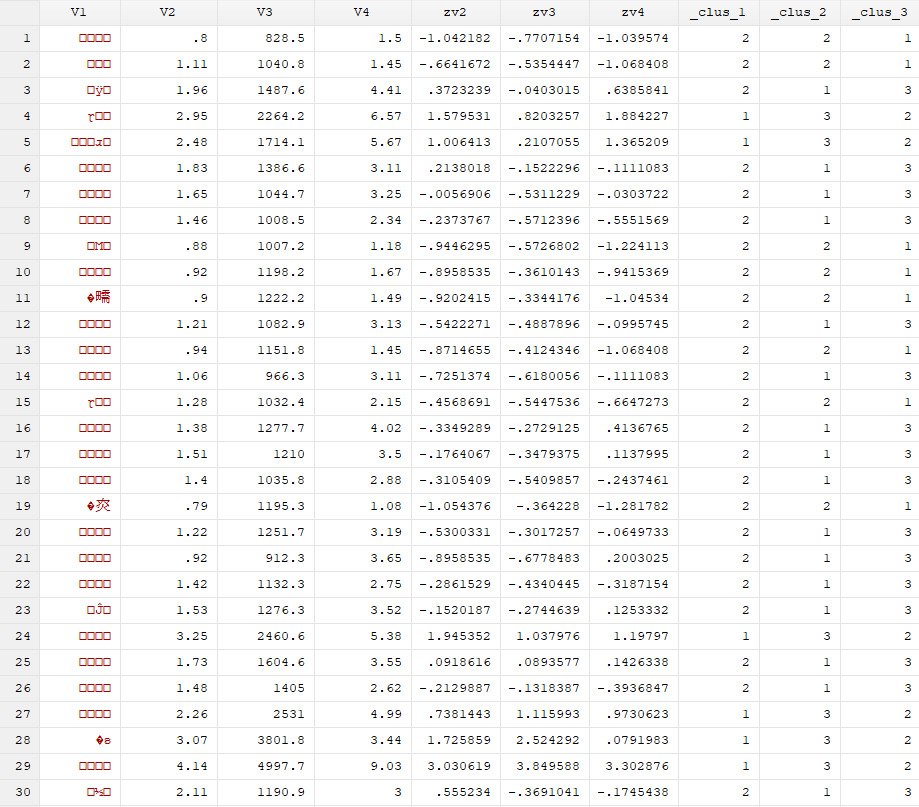
打开上方的数据浏览界面: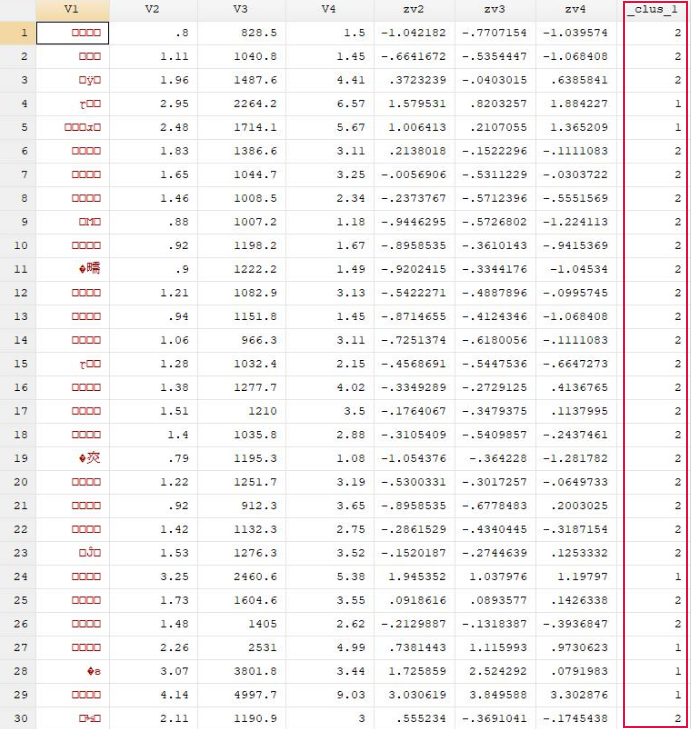 结果分析:可以看到数据被分为了1类和2类,观察每个分类特征,可以看到1类的变量zv2,zv3,zv4的值大都是比2类的高,基本是正数。 也可以分为三类:cluster kmeans zv2 zv3 zv4,k(3)
结果分析:可以看到数据被分为了1类和2类,观察每个分类特征,可以看到1类的变量zv2,zv3,zv4的值大都是比2类的高,基本是正数。 也可以分为三类:cluster kmeans zv2 zv3 zv4,k(3)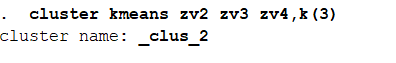
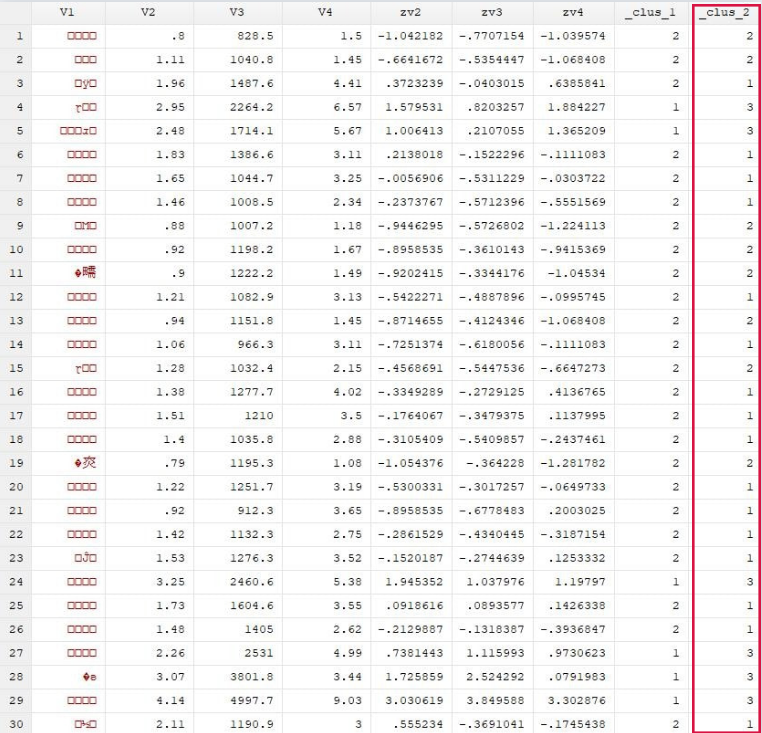 接下来介绍另外一种分类方法,按中位数划分聚类层次: cluster kmedians zv2 zv3 zv4,k(2)
接下来介绍另外一种分类方法,按中位数划分聚类层次: cluster kmedians zv2 zv3 zv4,k(2)
 02 层次聚类分析法 层次聚类分析法是根据一定标准使最相近的样本聚合在一起,然后逐步放松标准使得比较相近的样本汇集到一起,最后将所有观测样本都聚类分析到一个组。与划分聚类分析法的区别在于,它不用事先指定需要的分类的数量。方法共有6种:最短连接法聚类分析,最长连接法聚类分析,平均连接法聚类分析,加权平均法聚类分析,中位数连接法聚类分析,重心连接法聚类分析,wards连接聚类分析法。
02 层次聚类分析法 层次聚类分析法是根据一定标准使最相近的样本聚合在一起,然后逐步放松标准使得比较相近的样本汇集到一起,最后将所有观测样本都聚类分析到一个组。与划分聚类分析法的区别在于,它不用事先指定需要的分类的数量。方法共有6种:最短连接法聚类分析,最长连接法聚类分析,平均连接法聚类分析,加权平均法聚类分析,中位数连接法聚类分析,重心连接法聚类分析,wards连接聚类分析法。 首先还是对数据进行标准化处理,使其均值为0,标准值为1:
首先还是对数据进行标准化处理,使其均值为0,标准值为1:egen zv2=std(V2)
egen zv3=std(V3)
egen zv4=std(V4)
egen zv5=std(V5)
看看处理完的结果: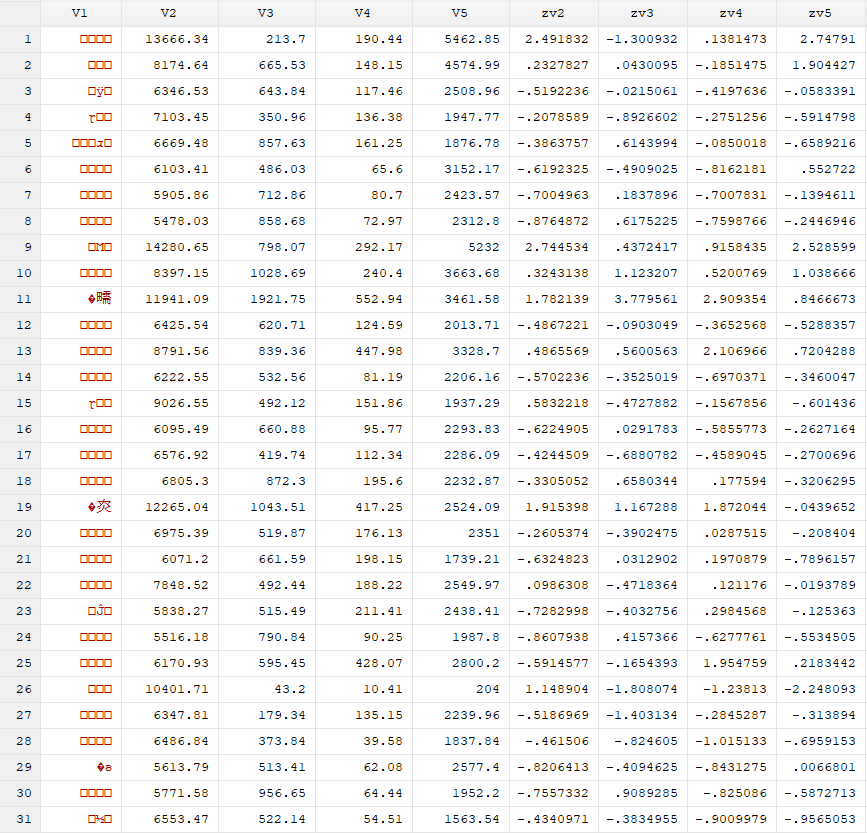 用最短连接法聚类分析方法对几个变量进行层次聚类分析: cluster singlelinkage zv2 zv3 zv4 zv5
用最短连接法聚类分析方法对几个变量进行层次聚类分析: cluster singlelinkage zv2 zv3 zv4 zv5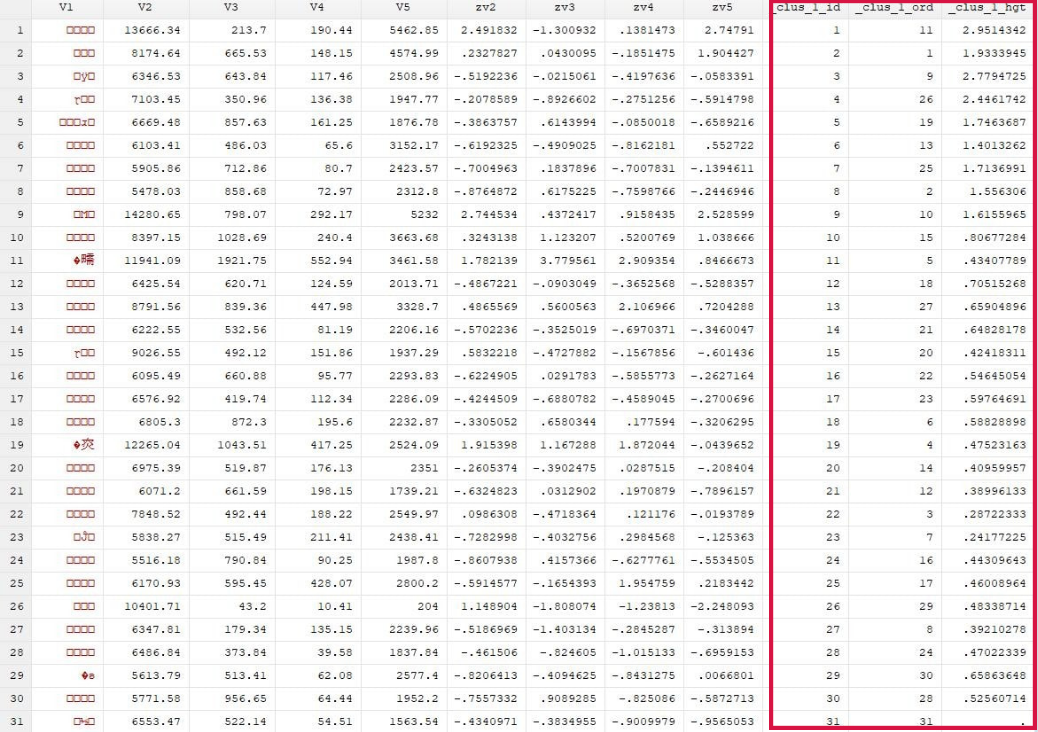 结果分析: clus_1_id表示系统对观测样本的初始编号,clus_1_ord表示系统对观测样本进行聚类分析处理后的编号,clus_1_hgt表示系统对该观测样本进行聚类计算算后的值。 为了让数据分析结果更加可视化一点,做一个聚类分析树状图: cluster dendrogram
结果分析: clus_1_id表示系统对观测样本的初始编号,clus_1_ord表示系统对观测样本进行聚类分析处理后的编号,clus_1_hgt表示系统对该观测样本进行聚类计算算后的值。 为了让数据分析结果更加可视化一点,做一个聚类分析树状图: cluster dendrogram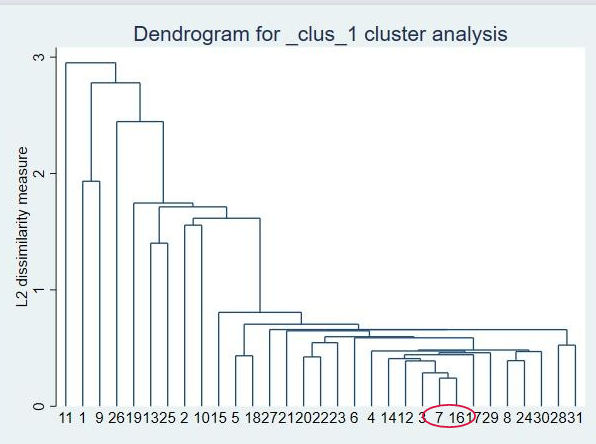 图形分析:我们抽取两个样本看,例如7号样本和16号样本是聚合在一起的,它两聚合后在一起后又与3号样本进行了聚合。依次类推,到最后11号样本和所有样本都聚集到了一块。那关于聚类可以分为几类呢,这个应依据自己研究需要,需要用户自己判断。例如你分两类,那么就以11号为一类,其余的为另一类。要分三类的话又是另外的分法。由此可见层次聚类分析法非常好的满足了聚类分析的探索性特点。 我们还可以用最长连接分析法: cluster completelinkage zv2 zv3 zv4 zv5 cluster dendrogram
图形分析:我们抽取两个样本看,例如7号样本和16号样本是聚合在一起的,它两聚合后在一起后又与3号样本进行了聚合。依次类推,到最后11号样本和所有样本都聚集到了一块。那关于聚类可以分为几类呢,这个应依据自己研究需要,需要用户自己判断。例如你分两类,那么就以11号为一类,其余的为另一类。要分三类的话又是另外的分法。由此可见层次聚类分析法非常好的满足了聚类分析的探索性特点。 我们还可以用最长连接分析法: cluster completelinkage zv2 zv3 zv4 zv5 cluster dendrogram
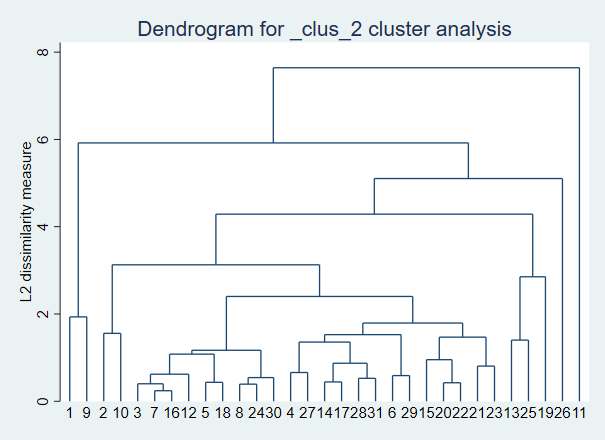 再试试平均连接法: cluster averagelinkage zv2 zv3 zv4 zv5 cluster dendrogram
再试试平均连接法: cluster averagelinkage zv2 zv3 zv4 zv5 cluster dendrogram
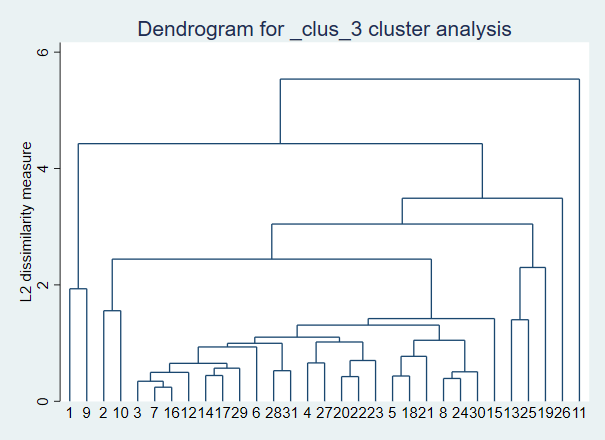 加权平均连接法: cluster waveragelinkage zv2 zv3 zv4 zv5 cluster dendrogram
加权平均连接法: cluster waveragelinkage zv2 zv3 zv4 zv5 cluster dendrogram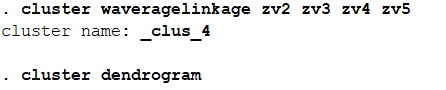
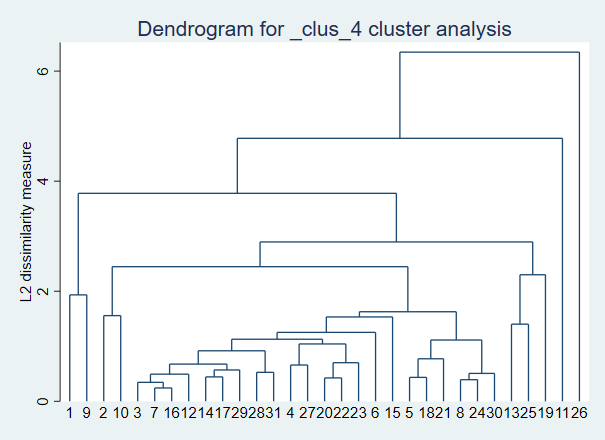 中位数连接法: cluster medianlinkage zv2 zv3 zv4 zv5 cluster dendrogram
中位数连接法: cluster medianlinkage zv2 zv3 zv4 zv5 cluster dendrogram
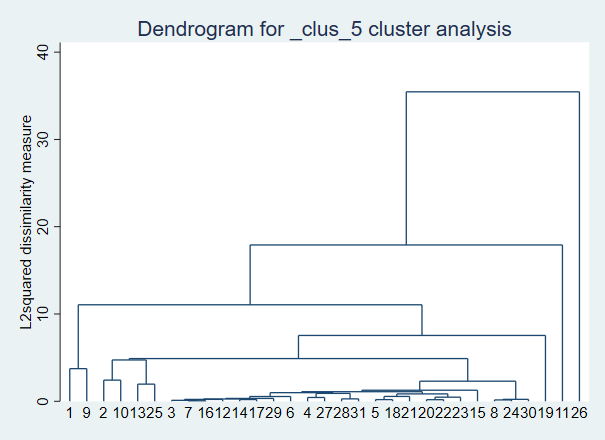 重心连接法聚类分析:cluster centroidlinkage zv2 zv3 zv4 zv5 这个无法画图。 wards连接聚类分析法: cluster wardslinkage zv2 zv3 zv4 zv5 cluster dendrogram
重心连接法聚类分析:cluster centroidlinkage zv2 zv3 zv4 zv5 这个无法画图。 wards连接聚类分析法: cluster wardslinkage zv2 zv3 zv4 zv5 cluster dendrogram
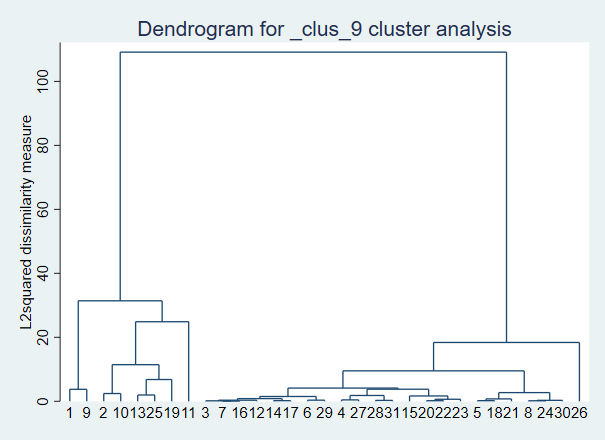 有时候样本比较多,所以做的图会比较乱,我们使用产生聚类变量的方法按照变量的特点对所有样本进行聚类,比如把所有样本分成四类,然后在进行层次聚类分析并作图: cluster generate type1=group(4)
有时候样本比较多,所以做的图会比较乱,我们使用产生聚类变量的方法按照变量的特点对所有样本进行聚类,比如把所有样本分成四类,然后在进行层次聚类分析并作图: cluster generate type1=group(4)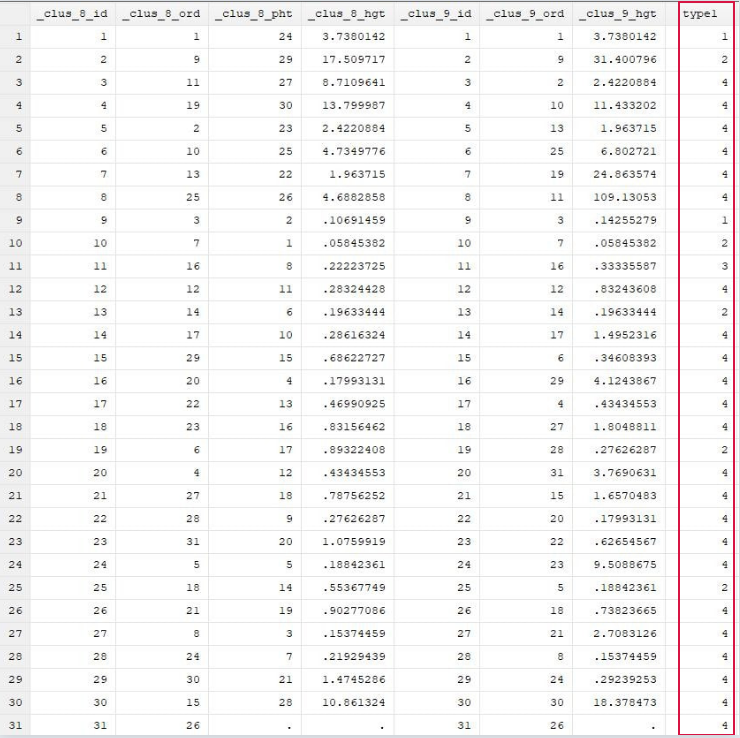
 在聚类分析法中,主要是划分聚类分析法和层次聚类分析法,前者程序比较简单,但后一种提供了很多方法,更方便按需去分析数据。接下来学习OLS回归分析。 OLS回归分析
在聚类分析法中,主要是划分聚类分析法和层次聚类分析法,前者程序比较简单,但后一种提供了很多方法,更方便按需去分析数据。接下来学习OLS回归分析。 OLS回归分析  最普通的最小二乘线性回归分析是分析某一变量受别的变量影响程度。基本思想是研究因变量和自变量的因果关系。主要有:简单线性回归、多重线性回归。 01 简单线性回归 简单线性回归只涉及一个自变量,建立变量之间的线性模型,并依据模型做出评价和预测。
最普通的最小二乘线性回归分析是分析某一变量受别的变量影响程度。基本思想是研究因变量和自变量的因果关系。主要有:简单线性回归、多重线性回归。 01 简单线性回归 简单线性回归只涉及一个自变量,建立变量之间的线性模型,并依据模型做出评价和预测。 在回归分析之前,先作描述性分析:summarize year inflation unwork,detailk 得到结果如下:
在回归分析之前,先作描述性分析:summarize year inflation unwork,detailk 得到结果如下: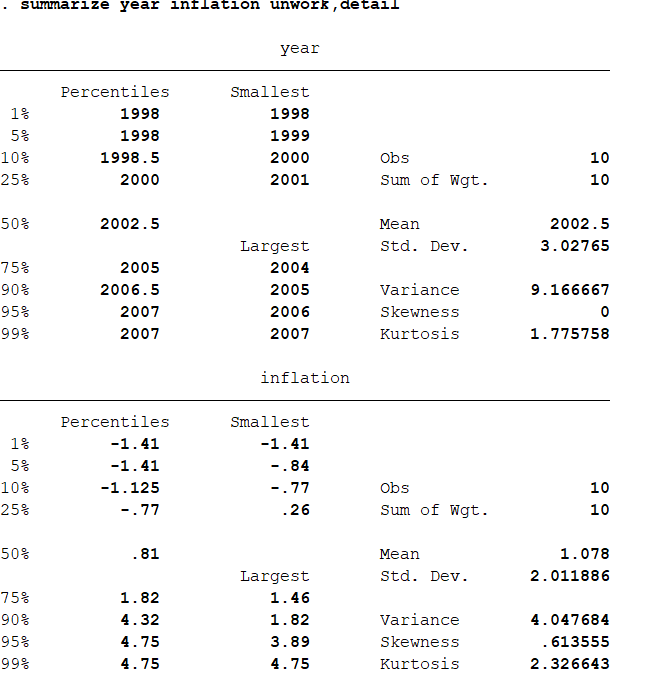
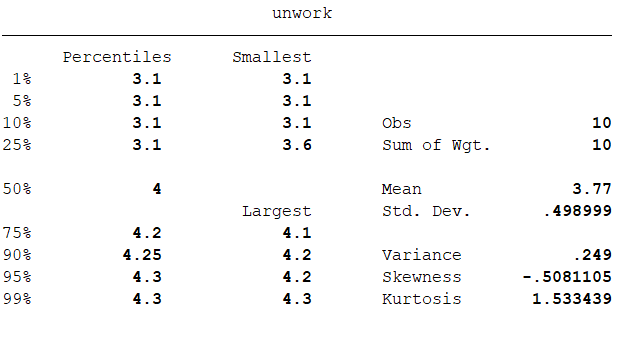 结果分析:通过本部分操作来了解数据的整体特征。看看有没有极端值,异常值。可以看到我们的数据质量还是不错的,变量之间的差距是可以接受的,变量的偏度,峰度也是可以接受的,可以进行下一步分析。 相关分析:correlate year inflation unwork
结果分析:通过本部分操作来了解数据的整体特征。看看有没有极端值,异常值。可以看到我们的数据质量还是不错的,变量之间的差距是可以接受的,变量的偏度,峰度也是可以接受的,可以进行下一步分析。 相关分析:correlate year inflation unwork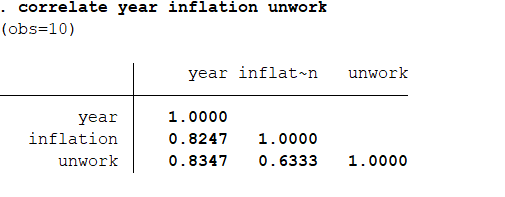 结果分析:通常来说一个变量可以影响另一个变量,那么他们之间是可能相关的关系。相关分析是回归分析很重要的一部分。但要注意数据分析作为辅助工具,可以验证事实,却不能推出事实。可以看出通货膨胀率和事业率的系数是0.633,说明这两个变量存在比较强的正相关关系。 下面进入回归分析,以失业率为因变量,通货膨胀率为自变量: regress unwork inflation
结果分析:通常来说一个变量可以影响另一个变量,那么他们之间是可能相关的关系。相关分析是回归分析很重要的一部分。但要注意数据分析作为辅助工具,可以验证事实,却不能推出事实。可以看出通货膨胀率和事业率的系数是0.633,说明这两个变量存在比较强的正相关关系。 下面进入回归分析,以失业率为因变量,通货膨胀率为自变量: regress unwork inflation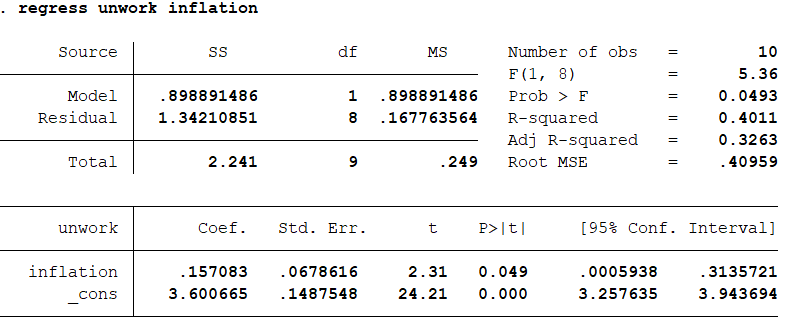 结果分析:模型的F值为5.36,P值为0.0493整体是非常显著的,在0.05的假设水平上通过了检验。模型的R系数为0.4011,修正系数为0.3263,说明模型的解释能力不足。模型的回归方程式:unwork=0.157083inflation+3.600665。其中自变量的系数标准误差是0.157083。t值是2.31,P值是0.049说明模型是非常显著的。我们还可知道95%的置信区间是多少。由此我们知道我国的通货膨胀率和失业率是正比关系。 获取参与回归的各变量的系数以及常数项的方差、协方差矩阵:vce
结果分析:模型的F值为5.36,P值为0.0493整体是非常显著的,在0.05的假设水平上通过了检验。模型的R系数为0.4011,修正系数为0.3263,说明模型的解释能力不足。模型的回归方程式:unwork=0.157083inflation+3.600665。其中自变量的系数标准误差是0.157083。t值是2.31,P值是0.049说明模型是非常显著的。我们还可知道95%的置信区间是多少。由此我们知道我国的通货膨胀率和失业率是正比关系。 获取参与回归的各变量的系数以及常数项的方差、协方差矩阵:vce 我们还可以进行变量系数的F检验:test inflation
我们还可以进行变量系数的F检验:test inflation 我们还可以对因变量的拟合值进行预测:predict yhat
我们还可以对因变量的拟合值进行预测:predict yhat
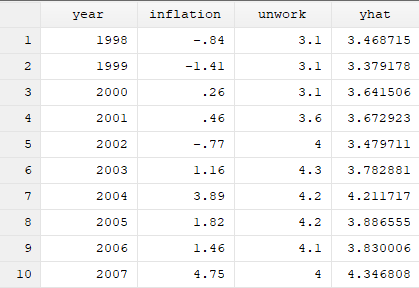 结果分析:因变量的预测拟合值是根据自变量的值代入我们建立的回归方程之中建立出的。 我们还可以得到残差序列:predict e,resid
结果分析:因变量的预测拟合值是根据自变量的值代入我们建立的回归方程之中建立出的。 我们还可以得到残差序列:predict e,resid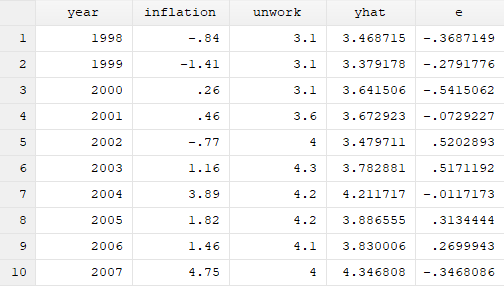 结果分析:得到的残差序列即是未被解释的部分,残留下来的东西。它是非常有用的,可以用来检验变量是否存在异方差,可以用来检验变量是否存在向量关系。 如果我们在建立回归模型不想要常数项:regress unwork inflation,nocon
结果分析:得到的残差序列即是未被解释的部分,残留下来的东西。它是非常有用的,可以用来检验变量是否存在异方差,可以用来检验变量是否存在向量关系。 如果我们在建立回归模型不想要常数项:regress unwork inflation,nocon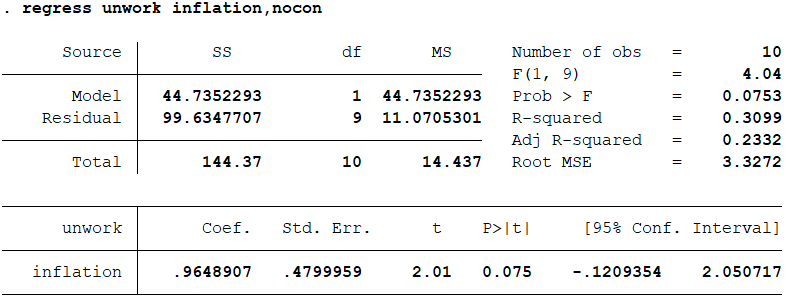
 02 多重线性回归分析 多重线性回归分析涉及多个变量,用来处理一个因变量和多个自变量之间的关系。应用最广泛的一种。
02 多重线性回归分析 多重线性回归分析涉及多个变量,用来处理一个因变量和多个自变量之间的关系。应用最广泛的一种。 进行简单的描述性分析:summarize TC Q PL PF PK 得到结果如下:
进行简单的描述性分析:summarize TC Q PL PF PK 得到结果如下: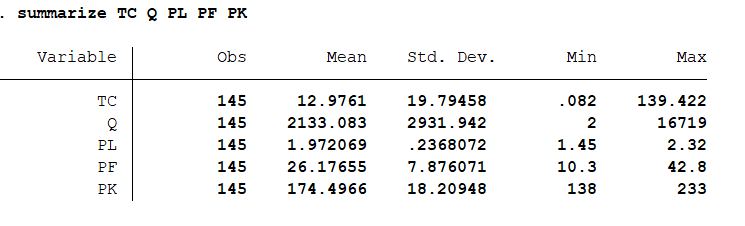 进行相关性分析:correlate TC Q PL PF PK
进行相关性分析:correlate TC Q PL PF PK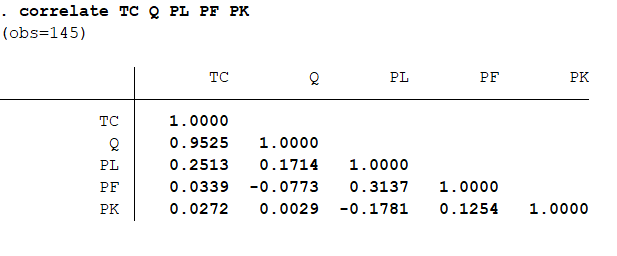 再进行回归分析:regress TC Q PL PF PK
再进行回归分析:regress TC Q PL PF PK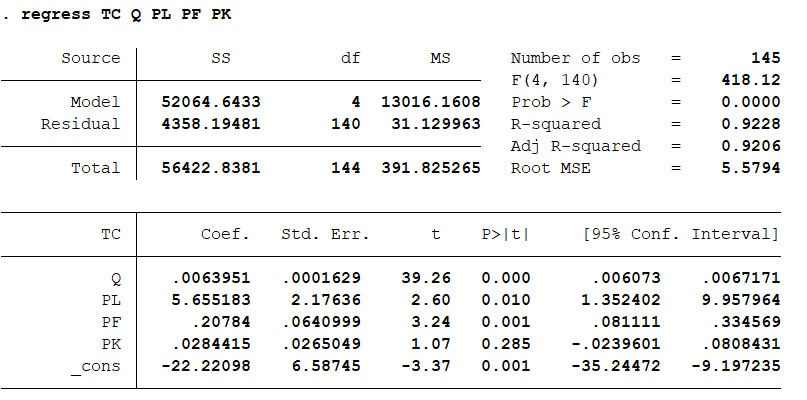 结果分析:F值为418.12,P值为0,说明模型是非常显著的。R值超过92%。说明模型的解释力度很强。下表明确了各自变量的系数,标准误差,t值,P值。可以看出,只有PK的P值,模型不是很显著。同时确定了模型的方程式。 获取方差和协方差矩阵:vce
结果分析:F值为418.12,P值为0,说明模型是非常显著的。R值超过92%。说明模型的解释力度很强。下表明确了各自变量的系数,标准误差,t值,P值。可以看出,只有PK的P值,模型不是很显著。同时确定了模型的方程式。 获取方差和协方差矩阵:vce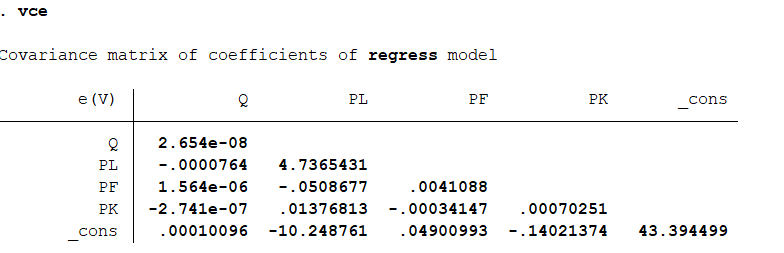 进行来联合系数检验,即构建所有自变量系数为零的检验:test Q PL PF PK
进行来联合系数检验,即构建所有自变量系数为零的检验:test Q PL PF PK 结果分析:P值为0,显著地拒绝了原假设:模型的自变量系数为0。 对因变量的拟合值进行预测:predict yhat
结果分析:P值为0,显著地拒绝了原假设:模型的自变量系数为0。 对因变量的拟合值进行预测:predict yhat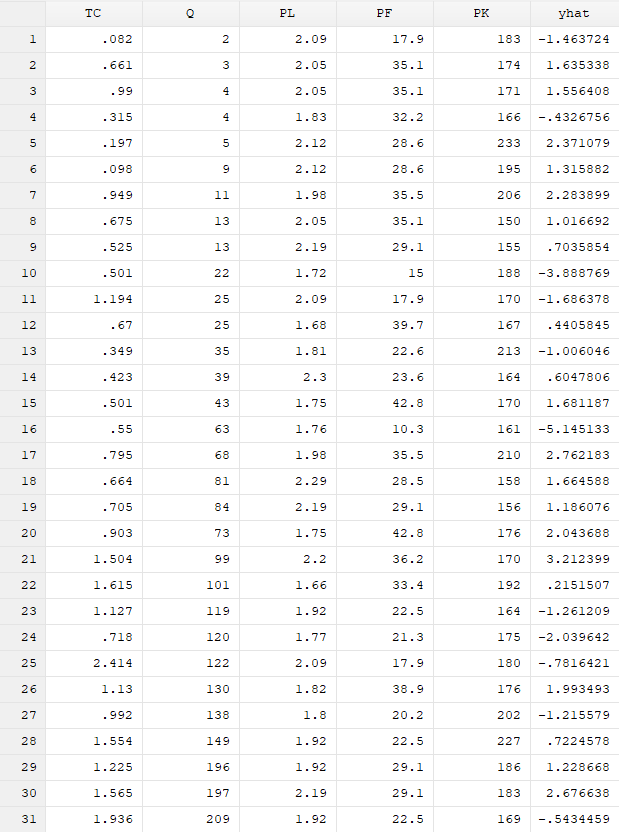 获取回归得到的残差序列:predict e,resid
获取回归得到的残差序列:predict e,resid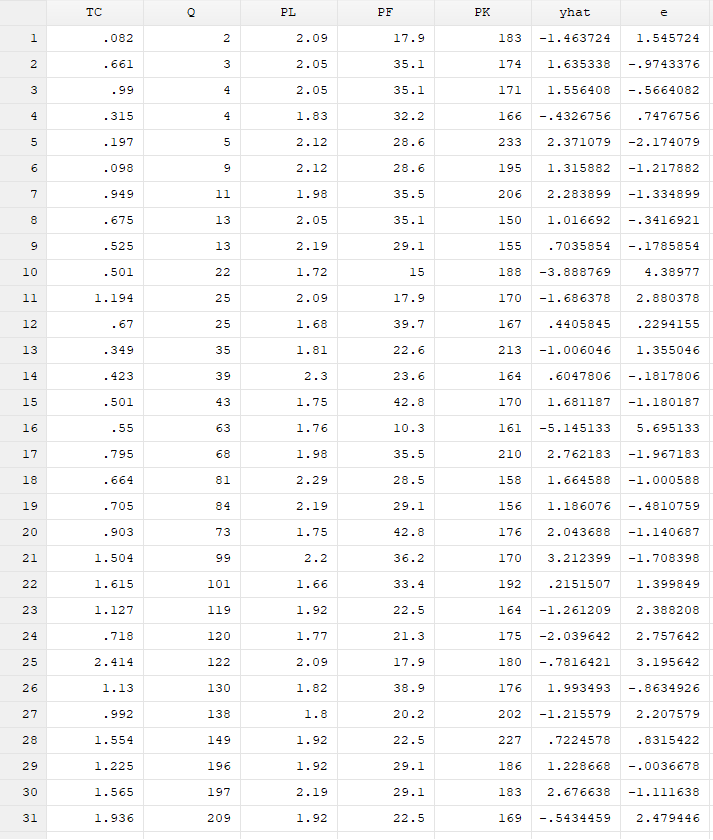 因为前面我们发现PK是不显著的,所以我们可以试试把PK剔除掉,重新进行回归: regress TC Q PL PF
因为前面我们发现PK是不显著的,所以我们可以试试把PK剔除掉,重新进行回归: regress TC Q PL PF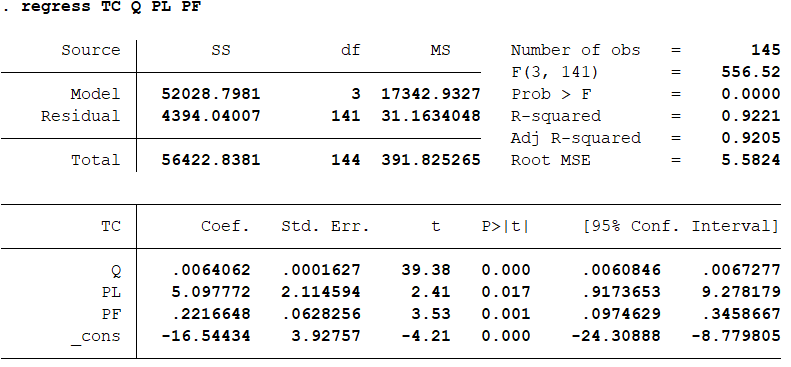 结果分析:发现剔除PK后,模型简直接近完美。我们可以此作为最终回归模型方程。
结果分析:发现剔除PK后,模型简直接近完美。我们可以此作为最终回归模型方程。 好啦,今天的学习到这里!如果有什么不懂,或者需要软件和教学资源请到后台联系我。
好啦,今天的学习到这里!如果有什么不懂,或者需要软件和教学资源请到后台联系我。- End -
“如果喜欢这期内容 那么请关注我吧”
版权声明:本文为weixin_31496135原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。