目录
〇,幻方
幻方一般指平面幻方,在一个n*n的表格中填入1,2,3,...,n^2,使得每一行每一列以及2条对角线的和都是相等的。
一,幻方的轮胎模型
把一个n*n的表格平面,上下相接,左右相接,变成一个轮胎。
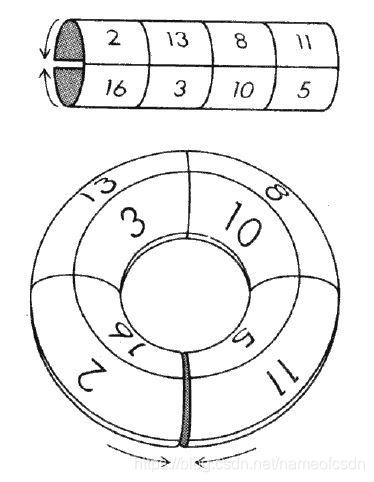
二,奇数阶幻方的构造法
1,罗伯构造法

这个方法构造出的五阶幻方:
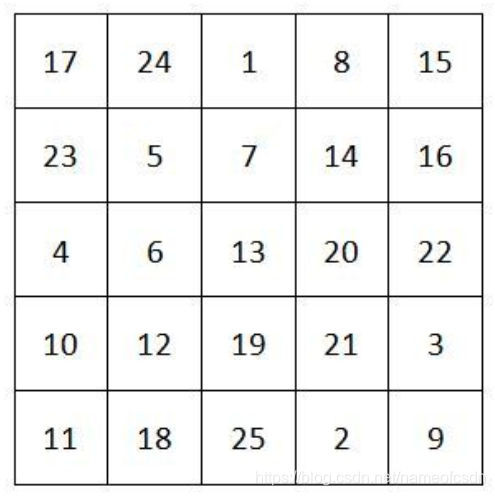
2,罗伯构造法的推广
从1开始,往右上移动的时候,可以每一次往右移动一列往上移动m行,只要(m,n)=1即可。
如m=2:

还有2点:

3,巴舍构造法(平移补空法)
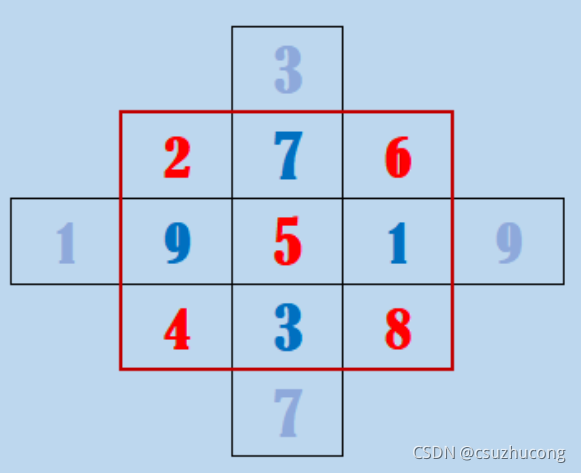
我理解本质上和罗伯构造法是一样的,只是表述方式和操作方式不一样。
准确的说,罗伯构造法的推广能构造出的幻方,应该是覆盖了巴舍构造法能构造出的幻方的。
4,轮换叠加构造法
取x, y 使得x, y, x+y 都和n互质,构造x左移方阵A和y右移方阵B:第一行写1到n的数字,后面每一行都是上一行的平移。
比如x=2, y=2, n=5


第一行的限制:如果x=1,则A右上角必须是中位数,如果y=1,则B左上角必须是中位数。
C是一个固定的方阵,所有格子都是1,
那么,n(B-C)+A就是幻方。

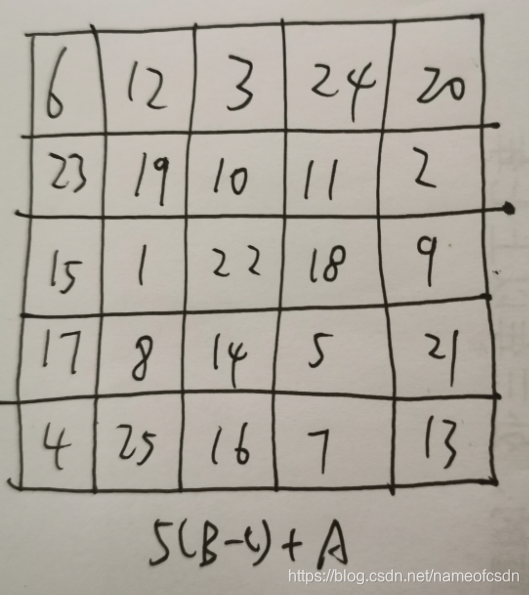
三,偶数阶幻方
1,n=4k的构造法
(1)按顺序填入数字
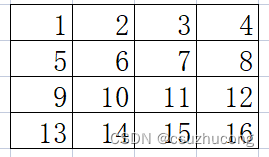
(2)把整个矩阵分成k^2个4*4的小矩阵,把每个小矩阵中的这8个位置进行调整
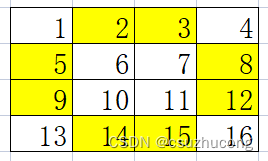
调整方法是把x换成n^2+1-x
四,幻立方
1,幻立方
把1,2,3,...,n^3填入一个n*n*n的三维表格,使得n^2个列,n^2个行,n^2个竖直列,以及4条对角线上数字之和都相等。
显然,这个和是(n^3+1)*n/2
2,完美幻立方
如果一个幻立方满足,3n个截面上的2条对角线的数字之和也都等于(n^3+1)*n/2,那么称之为完美幻立方。
4阶完美幻立方:
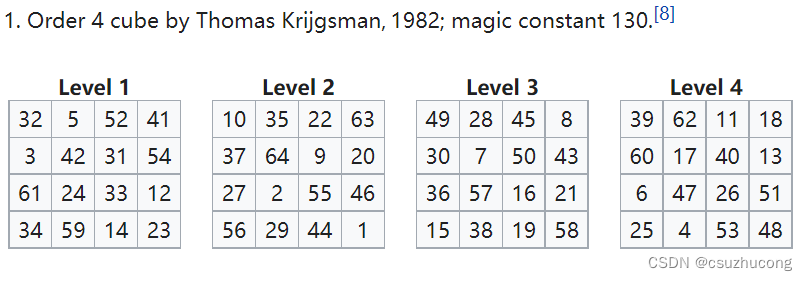
5阶完美幻立方:
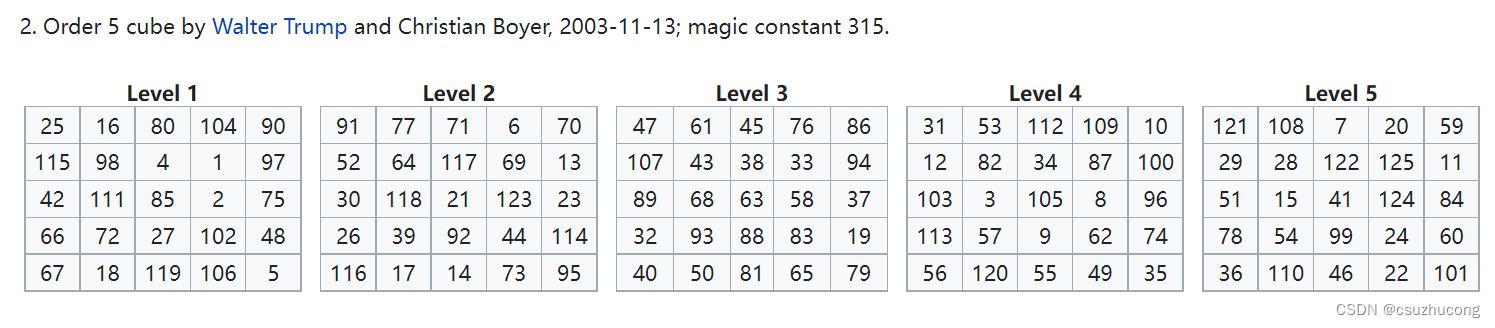
五,OJ实战
HDU 1998 奇数阶魔方
题目:
Description
一个 n 阶方阵的元素是1,2,...,n^2,它的每行,每列和2条对角线上元素的和相等,这样 的方阵叫魔方。n为奇数时我们有1种构造方法,叫做“右上方” ,例如下面给出n=3,5,7时 的魔方.
3
8 1 6
3 5 7
4 9 2
5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
7
30 39 48 1 10 19 28
38 47 7 9 18 27 29
46 6 8 17 26 35 37
5 14 16 25 34 36 45
13 15 24 33 42 44 4
21 23 32 41 43 3 12
22 31 40 49 2 11 20
第1行中间的数总是1,最后1行中间的数是n^2,他的右边是2,从这三个魔方,你可看出“右上方”是何意。
Input
包含多组数据,首先输入T,表示有T组数据.每组数据1行给出n(3<=n<=19)是奇数。
Output
对于每组数据,输出n阶魔方,每个数占4格,右对齐
Sample Input
2
3
5
Sample Output
8 1 6
3 5 7
4 9 2
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
这个题目规定死了填的方式,直接写出来就是的了。
用了一个小技巧,不需要记录区分哪些格子已经写过了,哪些没写过。
什么时候会遇到右上方已经写了数的情况,直接根据num就可以算出来
因为我对幻方做过一点研究,所以应该算是写的比较简洁的。
代码:
#include<iostream>
#include<iomanip>
using namespace std;
int matrix[20][20];
int main()
{
int t, n;
cin >> t;
while (t--)
{
cin >> n;
int number = 1, line = 1, column = n / 2 + 1;
while (number<=n*n)
{
matrix[line][column] = number++;
if (number%n == 1)line++;
else
{
line = (line + n - 2) % n + 1;
column = column%n + 1;
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)cout << setw(4) << matrix[i][j];
cout << endl;
}
}
return 0;
}HDU 2183 奇数阶魔方(II)
题目:
Description
1 ,2, 3, …,n^2 这n^2 个数 排成n*n 方阵 每行每列每条对角线上的n个数字之和s相等,
s=n(n*n+1)/2,奇数阶魔方可由菱形转变成
n=3,5时如下
3
*********1
******4******2
***7*****5******3
******8******6
*********9
4 9 2
3 5 7
8 1 6
5
*******************1
***************6*******2
**********11*******7*******3
******16*******12*******8*******4
**21******17******13*******9*******5
******22*******18*****14******10
**********23*******19******15
**************24******20
******************25
11 24 7 20 3
4 12 25 8 16
17 5 13 21 9
10 18 1 14 22
23 6 19 2 15
Input
输入奇数 3<=n<=21. n=0退出
Output
输出n阶魔方,每个数字占4列,右对齐
Sample Input
7
0
Sample Output
22 47 16 41 10 35 4
5 23 48 17 42 11 29
30 6 24 49 18 36 12
13 31 7 25 43 19 37
38 14 32 1 26 44 20
21 39 8 33 2 27 45
46 15 40 9 34 3 28
代码:
#include<iostream>
#include<iomanip>
using namespace std;
int matrix[22][22];
int main()
{
int n;
while (cin >> n)
{
if (n == 0)break;
int number = 1, line = n / 2 + 2, column = n / 2 + 1;
while (number<=n*n)
{
matrix[line][column] = number++;
if (number%n == 1)line = (line + 1) % n + 1;
else
{
line = line % n + 1;
column = column % n + 1;
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)cout << setw(4) << matrix[i][j];
cout << endl;
}
}
return 0;
}六,幻圆
1,直径幻圆
要求每一个圆圈的数字之和相等,每一条直径的数字之和相等。
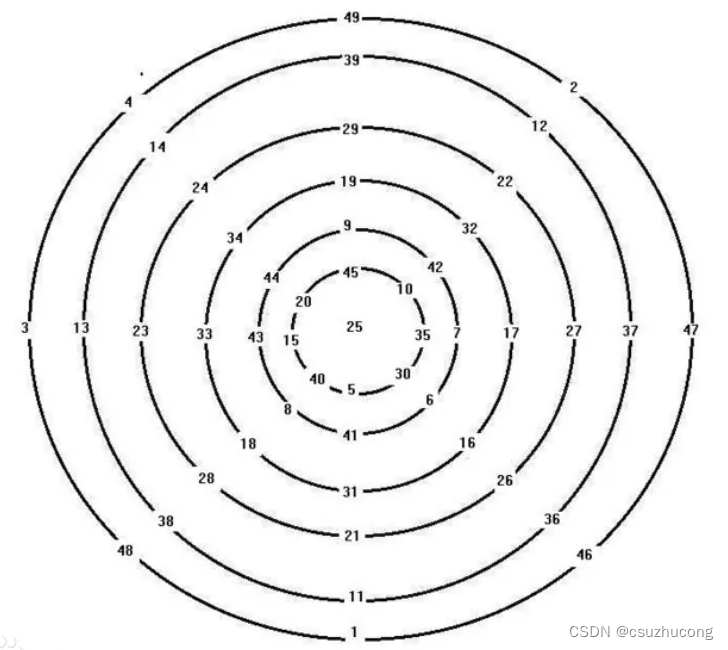
这里面是1-49,除掉25之外是6*8=48个数
2,半径幻圆
半径幻圆比直径幻圆更严格,要求每一条半径的数字之和相等。
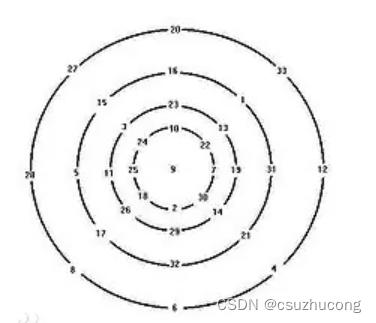
把圆变成矩形,半径幻圆的要求就变成,矩形的每一行之和相等,每一列之和相等,比幻方的要求还是要略低。
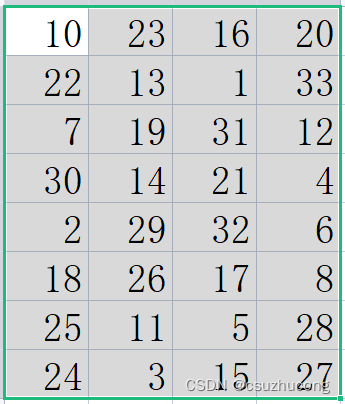
这里面是1-33,排除9
七,拉丁方
1,拉丁方
在这种 n × n 的方阵里,恰有 n 种不同的元素,每一种不同的元素在同一行或同一列里只出现一次。
数独也是一种拉丁方。
显然,拉丁方有朴素通解。
2,正交拉丁方
把一个 n × n 的方阵A中的元素,填入到方阵B,使得B中的每一行n个元素在A中的对应位置,没有2个元素在同一行或同一列,同理,B中的每一列n个元素在A中的对应位置,没有2个元素在同一行或同一列。
据悉,除了n=2,6之外,n阶正交拉丁方都存在。
4阶正交拉丁方:
