课程链接
之前我们已经介绍了线性回归问题,分类问题是不适用线性回归方法的。
理想情况下的分类问题的解决
模型是一个布尔函数,损失函数是分类错误的次数,这样的损失函数显然是不能用最优化方法求解的。不过它也可以用感知机和支持向量机来解决,本节不作介绍。
因此我们在这里采用概率统计的方法进行求解,算出某一项数据落入某一类的最大可能性。
比较简单和常用的分布是高斯分布。建立高斯分布只需要数据的均值和方差。
在课程中我们待解决的问题是通过宝可梦的攻击防御等属性对宝可梦分类。输入7种属性分别计算均值方差的情况下分类水系和一般系宝可梦效果并不理想。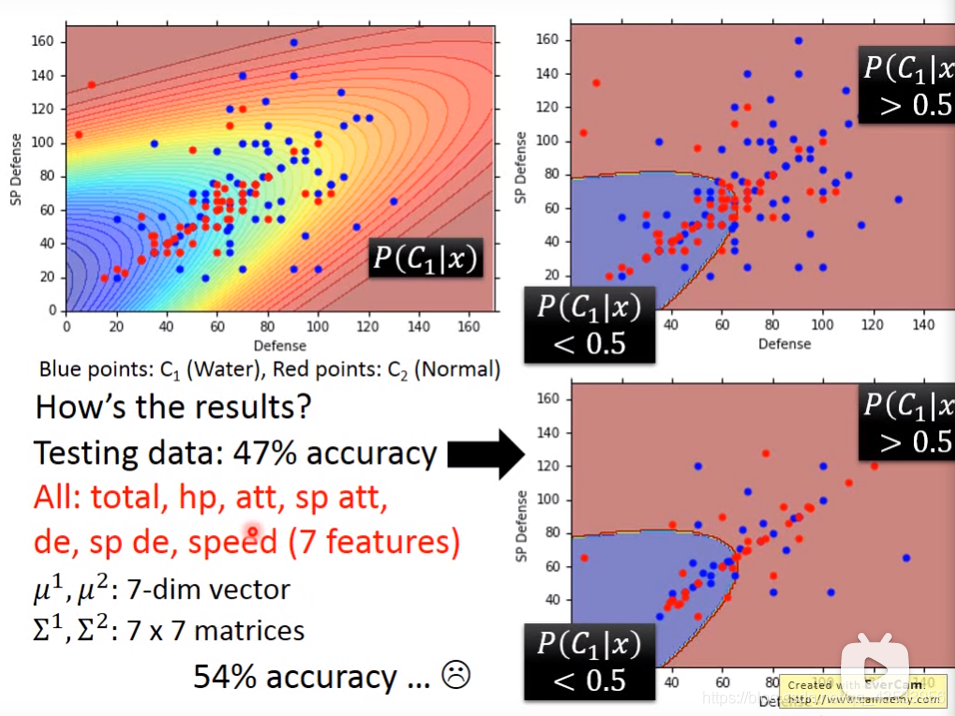
我们猜测(不一定对)可能是模型过于复杂出现的过拟合现象。简化模型假设每种属性正态分布只有均值不同,方差是共享的。
在这样改进之后,分类的边界变成里直线,准确率也有了一定的提升。
逻辑回归
虽然线性回归无法解决分类问题,但是,逻辑回归可以。
通过上图中的公式转换,我们可以把x落入C1的概率,写成关于z的sigmoid函数(sigmoid函数可以把一个任意实数转化到(0,1)之间)。
z的形式和回归中的模型是一样的,因此我们把sigmoid(z)作为逻辑回归的第一步的模型。
第二步是根据模型得到一个损失函数,这里用到了最大似然估计。
最大似然估计是根据我们已经有的采样数据,求子事件p使得采样的事件发生的可能性最大。
为了计算方便我们把arg max(L)转化成等价的arg min(-lnL)。设现在有两类C1C2,落入C1则y值为1,否则为0。(两类分类实际上就可以看做是伯努利分布)。
最后公式推导得到的蓝线上的结果就是伯努利分布的交叉熵。当模型与真实情况完全相同时,交叉熵就是0.
交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。
有了损失函数,第三步就是通过损失函数求出最合适的w和b参数了。
第三步的求解,逻辑回归和线性回归是完全相同的。
平方误差VS交叉熵
平方误差在处理分类问题时,可能会出现当离最低点很远时下降很慢的情况,如图所示。
生成模型VS判别模型

直接求解参数w和b的模型称为判别模型,而预设其概率分布的模型称为生成模型。
生成模型中预设的误差常常会影响模型本身的准确性,所以准确度往往不如判别模型。但是生成模型也有其优势。
生成模型需要的训练数据更少,抗噪声性能也更好。
三类分类的逻辑回归
先对三类分别建立 z模型。
将z1,z2,z3分别带入softmax函数,得到y1,y2,y3,再把它们和训练数据计算交叉熵。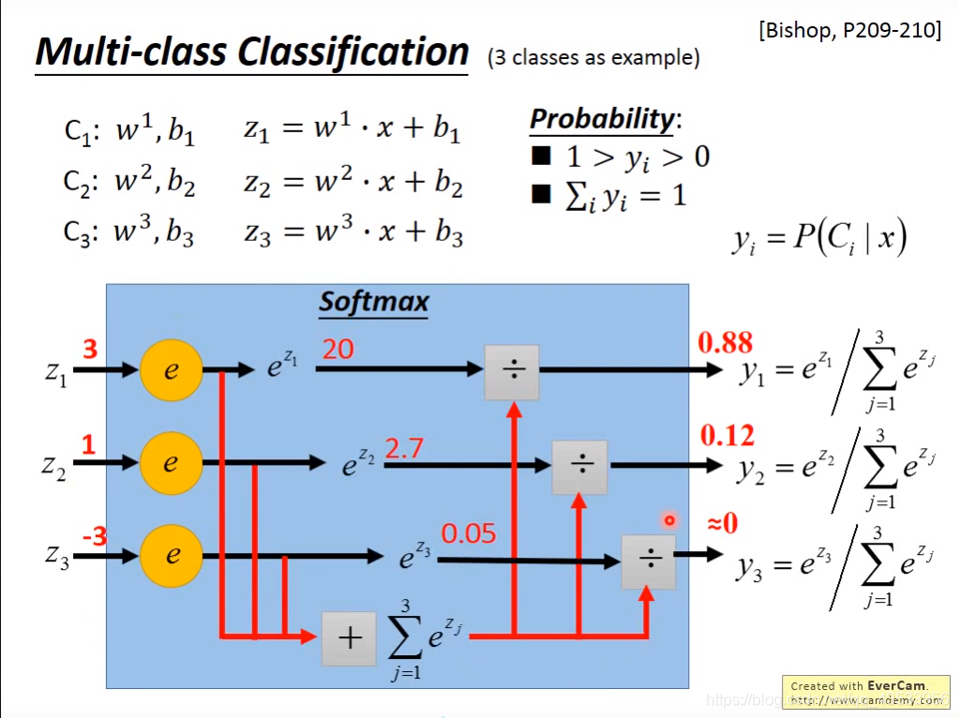

逻辑回归的限制性
逻辑回归要求两类之间必须有一条分界线,如果存在交叉,则不能直接求解。