python解析法求解多元线性问题

课程链接

链接: link.

解析法求一多元线性

求面积、房间数对房价的关系，其中面积与房价，房间数与房价都是线性关系

理论基础

求解问题：求一理想直线最能描述样本点增长趋势

具体：求 W 矩阵

基本思想：与一元线性回归问题相同

适用条件：
每个影响因素(例如面积、房间数)与因变量(房价)是线性关系
X矩阵需满秩，不是满秩即影响因素过多或数据不足造成有多个W矩阵的解

代码

重要公式部分代码对照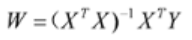


所有代码

import numpy as np

x1 = np.array([137.97, 104.50, 100.00, 124.32, 79.20, 99.00, 124.00, 114.00,
                 106.69, 138.05, 53.75,  46.91,  68.00, 63.02, 81.26,  86.21])
x2 = np.array([3,2,2,3,1,2,3,2,2,3,1,1,1,1,2,2])
y = np.array([145.00, 110.00, 93.00, 116.00,  65.32, 104.00, 118.00, 91.00,
                 62.00,  133.00, 51.00, 45.00,   78.50, 69.65,  75.69,  95.30])

x0 = np.ones(len(x1))
X = np.stack((x0,x1,x2),axis=1)

Y = np.array(y).reshape(-1,1)

# W = (X'X)-1X'Y
# np.matmul() 矩阵相乘
# np.transpose() 矩阵转置 X'
# np.linalg.inv() 矩阵求逆 X-1

Xt = np.transpose(X)
XtX_1 = np.linalg.inv(np.matmul(Xt,X))
XtX_1_Xt = np.matmul(XtX_1,Xt)
W = np.matmul(XtX_1_Xt,Y)

W=W.reshape(-1)
for i in range(len(W)):
    W[i] = round(W[i],3)

print("多元线性回归方程：")
print("Y=",W[1],"*x1+",W[2],"*x2+",W[0])

print("请输入房屋面积和房间数，预测房屋销售价格：")
x1_test = float(input("商品房面积："))
x2_test = float(input("房间数："))

y_pred = W[1]*x1_test+W[2]*x2_test+W[0]
print("预测价格：",round(y_pred,2),"万元")