交通灯说明
作为IC/FPGA应聘者,交通灯的verilog设计是必须掌握的基本技能。本文以典型交通灯为例,即在主干道和支路相交的十字路口,主干道具有较高优先级。首先,应该明确:
【1】除红灯外,其他有效灯转为另一个状态,中间都应设定黄灯作为缓冲,如:交通灯由绿灯转为左拐灯之前,应该有一段黄灯作为缓冲段,同理,如果左拐灯转为红灯,也应设定黄灯作为缓冲段;
【2】主干道处于红灯时,支路应处于非红灯的其他几个状态的转换过程,支路处于红灯时,主干道同理;
本文假定灯的状态包括:绿灯、黄灯、左拐,主干道绿灯亮40s,支路绿灯亮30s,画出各灯状态转换及亮的时间如下:
FSM建模
本交通灯没有外部输入信号,内部各个状态的转换与外界无关,按照图1 的时序,上一个状态结束(即亮灯的时间到),就跳入下一个状态,如此循环。故,设定一个计数器,对每一段状态按照既定的时长计时,在计数到最后1次时,产生状态跳转条件。本设计巧妙利用这一点,所有状态共用一个计数器,完成状态转换条件的产生。最后,在各个状态下,点亮相应的灯(即输出),因为输出只与当前状态有关,故交通灯采用moore状态机描述。同时,采用典型三段式FSM的描述方式,代码通俗易懂。
交通灯的三段式moore_FS描述如下:
module transport_lamp # (
parameter L_WID = 4 // 灯的个数
)(
input clk ,
input rst_n ,
// input start , // 触发信号
output [L_WID - 1 : 0] m_lamp , // 主干道从高到低分别表示:绿、黄、左、红
output [L_WID - 1 : 0] s_lamp // 同上
);
//-----------------------------功能说明------------------------------//
// 本交通灯描述经典交通灯,主干道和支干道各
// 主干道:绿(40s)黄(5s)左(15s)黄(5s) | 红(55s)----------------------
// 支干道:红(65s)------------------------| 绿(30s)黄(5s)左(15s)黄(5s)
// 说明:绿灯结束后过渡到红灯都设定黄灯停留作为警示;
// 在各自红灯区内,另一干道按照既定顺序执行绿、黄、左、黄,许多交通灯控制中常省略黄灯
// 状态机设计:采用计数器产生状态转移条件,输出只与当前状态有关——moore式FSM
//------------------------------------------------------------------//
localparam CNT_WID = 8;
reg [CNT_WID - 1 : 0] clk_cnt;
reg [3:0] state;
localparam s0_G_M = 4'd0,
s1_Y_M = 4'd1,
s2_L_M = 4'd2,
s3_Y_M2 = 4'd3,
s4_G_S = 4'd4,
s5_Y_S = 4'd5,
s6_L_S = 4'd6,
s7_Y_S2 = 4'd7;
localparam TIME_G_M = 8'd40,
TIME_Y = 8'd5,
TIME_L = 8'd15,
TIME_G_S = 8'd30;
// 第一段:描述状态转移条件和转移规律(组合逻辑)
assign go_s0 = state == s7_Y_S2 && clk_cnt == TIME_Y;
assign go_s1 = state == s0_G_M && clk_cnt == TIME_G_M;
assign go_s2 = state == s1_Y_M && clk_cnt == TIME_Y;
assign go_s3 = state == s2_L_M && clk_cnt == TIME_L;
assign go_s4 = state == s3_Y_M2 && clk_cnt == TIME_Y;
assign go_s5 = state == s4_G_S && clk_cnt == TIME_G_S;
assign go_s6 = state == s5_Y_S && clk_cnt == TIME_Y;
assign go_s7 = state == s6_L_S && clk_cnt == TIME_L;
// 公用计数器模块,用于产生状态转移的条件
always @ (posedge clk) begin: CLK_COUNT
if (!rst_n)
clk_cnt <= {CNT_WID{1'b0}};
else if (go_s0 | go_s1 | go_s2 | go_s3 | go_s4 | go_s5 | go_s6 | go_s7 )
clk_cnt <= {CNT_WID{1'b0}};
else
clk_cnt <= clk_cnt + 1'b1;
end
// 第二段:实现状态转移,采用时序逻辑
always @ (posedge clk) begin: STATE_CHANGE
if (!rst_n)
state <= s0_G_M;
else begin
case (state)
s0_G_M: state <= go_s1 ? s1_Y_M : s0_G_M;
s1_Y_M: state <= go_s2 ? s2_L_M : s1_Y_M;
s2_L_M: state <= go_s3 ? s3_Y_M2 : s2_L_M;
s3_Y_M2: state <= go_s4 ? s4_G_S : s3_Y_M2;
s4_G_S: state <= go_s5 ? s5_Y_S : s4_G_S;
s5_Y_S: state <= go_s6 ? s6_L_S : s5_Y_S;
s6_L_S: state <= go_s7 ? s7_Y_S2 : s6_L_S;
s7_Y_S2: state <= go_s0 ? s0_G_M : s7_Y_S2;
default: state <= s0_G_M;
endcase
end
end
// 第三段:描述输出(仅取决于当前状态——moore_FSM),可以采用组合逻辑(与所在状态同一拍),
// 也可以采用时序逻辑(下一拍输出),因为组合逻辑书写方便(故这样写)
assign m_lamp[3] = state == s0_G_M;
assign m_lamp[2] = state == s1_Y_M || state == s3_Y_M2;
assign m_lamp[1] = state == s2_L_M;
assign m_lamp[0] = state == s4_G_S || state == s5_Y_S || state == s6_L_S || state == s7_Y_S2;
assign s_lamp[3] = state == s4_G_S;
assign s_lamp[2] = state == s5_Y_S || state == s7_Y_S2;
assign s_lamp[1] = state == s6_L_S;
assign s_lamp[0] = state == s0_G_M || state == s1_Y_M || state == s2_L_M || state == s3_Y_M2;
endmodule
FSM仿真
仿真结果如下,整个时序安装既定时序执行。下图2中,选定一个周期内,共8个状态,黄色箭头描述个状态的转移规律,红色箭头表示红灯状态实际上由另一道路的其他状态(红灯除外)构成。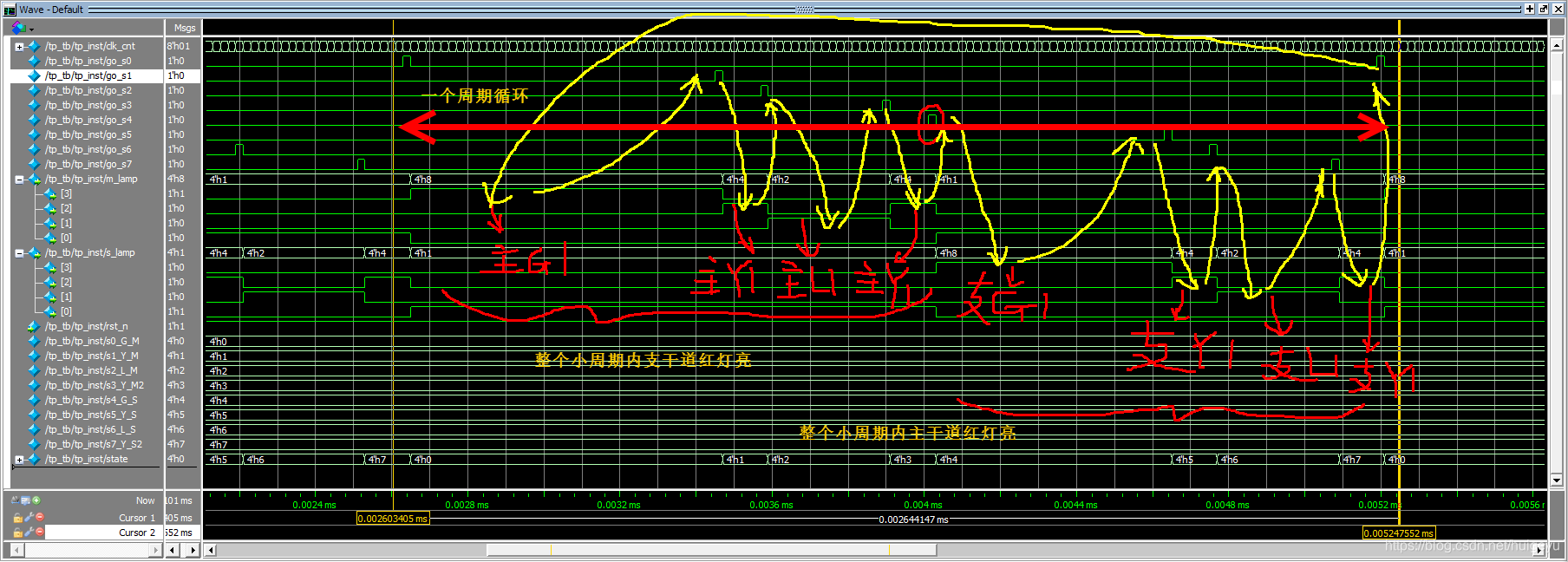
版权声明:本文为huigeyu原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。