USACO 2013 US Open Bronze 奶牛芭蕾 (图形学 矩阵坐标变换)

题目描述

为了挑战人们将奶牛视为笨拙生物的成见，农夫约翰的奶牛贝茜报名参加了芭蕾舞入门班。

她的最后一场演出是下周，约翰想帮她搭建一个足够大的长方形舞台，这样她就可以在不从舞台边沿跌落的情况下表演整个舞蹈。

贝茜的舞蹈将在一个长方形的舞台上进行，这个舞台可以看作由 1×1 的单元格组成的矩阵。

贝茜的四只脚被简明扼要地描述如下：

FR：右前脚
FL：左前脚
RR：右后脚
RL：左后脚

她的四只脚最开始位于四个相邻的单元格中，这四个单元格可以构成一个小正方形，如下所示，贝茜朝北站立：

FL FR
RL RR

贝茜的舞蹈遵循一系列 N 条指令，每条指令要么指示她将一只脚移动一个单元格，要么指示她顺时针转动 90 度。

移动脚的指令由 3 个字符组成，前两个字符表明要移动的脚，最后一个字符指定移动方向（F = 前进，B = 后退，R = 右，L = 左）。

例如，FRF 表示贝茜应该将她的右前脚向前移动一个单元格，RLR 表示她应该将她的左后脚向右移动一个单元格。

当然，运动的方向与贝茜面对的方向是相对的。

贝茜的顺时针转动是以某一只脚作为枢轴而进行的，转动时枢轴脚应保持竖立，并围绕该脚进行顺时针转动。

顺时针转动的指令也由 3 个字符组成，前两个字符表明枢轴脚，最后一个字符为 P，表示该脚作为枢轴。

例如，FRP 表示贝茜应该以右前脚作为枢轴，围绕其顺时针旋转 90 度。

这意味着，如果贝茜的脚现在处于如下位置（贝茜朝北站立）：

.. .. .. 
.. .. FR 
.. FL .. 
.. RL RR 

执行完 FRP 指令以后，她的脚将位于如下位置，贝茜现在朝东站立：

RL FL .. 
RR .. FR 
.. .. ..  
.. .. .. 

给定贝茜舞蹈的 N 条指令，请计算能够使贝茜全程不踩空跌落的长方形舞台的最小面积。

如果贝茜将一只脚移动到与另一只脚相同的单元格内，她就会被绊倒，从而无法完成舞蹈。

这种情况下，请输出 −1。

注意，这是贝茜唯一能够被绊倒的情况，在经过所有练习以后，贝茜十分灵活，很容易摆出各种高难度姿势（例如，后脚比前脚更向前）。

输入格式

第一行包含整数 N。

接下来 N 行，每行包含三个字符，表示一个舞蹈指令。

输出格式

输出在整个舞蹈过程中，能够容纳贝茜的脚所必须的长方形舞台的最小面积。

如果贝茜被绊倒，则输出 −1。

数据范围
$1\le N\le 1000$

输入样例：

3
FRF
FRP
RLB

输出样例：

16

样例解释

贝茜需要一个 4×4 大小的舞台，保证她能够完成她的舞蹈。

她的脚步如下：

.. .. .. .. 
.. .. .. .. (朝北)
.. .. FL FR 
.. .. RL RR 

执行 FRF 后：

.. .. .. .. 
.. .. .. FR (朝北)
.. .. FL .. 
.. .. RL RR 

执行 FRP 后：

.. RL FL .. 
.. RR .. FR (朝东)
.. .. .. .. 
.. .. .. .. 

执行 RLB 后：

RL .. FL ..
.. RR .. FR (朝东)
.. .. .. ..
.. .. .. ..

分析

本题目的关键问题在于矩阵顺时针旋转时的坐标变换：
$$\left[\begin{array}{c}{X}_{new}{Y}_{new}\end{array}\right]=\left[\begin{array}{c}{X}_{old}{Y}_{old}\end{array}\right]\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$$
由于本题目是旋转90°，所以把θ=90带入得到：
$$\left[\begin{array}{c}{X}_{new}{Y}_{new}\end{array}\right]=\left[\begin{array}{c}{X}_{old}{Y}_{old}\end{array}\right]\left[\begin{array}{cc}cos90& -sin90\\ sin90& cos90\end{array}\right]=\left[\begin{array}{c}{X}_{old}{Y}_{old}\end{array}\right]\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]=\left[\begin{array}{c}{Y}_{old}-X_{old}\end{array}\right]$$

每次旋转过后方向都会改变，我们默认朝前为0。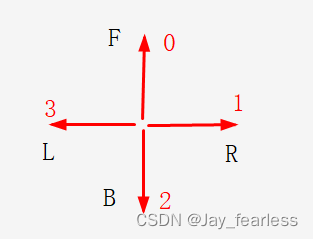

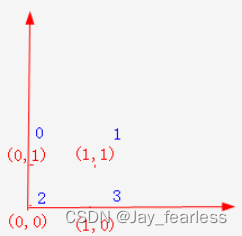
刚开始的四个脚的方位

C++ 代码

#include<bits/stdc++.h>

#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;

//定义初始四个坐标
PII p[4] = {{0, 1}, {1, 1}, {0, 0}, {1, 0}};
//定义刚开始的四个脚的方位
int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};
unordered_map<string, int> id = {{"FL", 0}, {"FR", 1}, {"RL", 2}, {"RR", 3}};
//定义转向的坐标
unordered_map<char, int> turn = {{'F', 0}, {'B', 2}, {'L', 3}, {'R', 1}};
int minx = 0, maxx = 1, miny = 0, maxy = 1;

//旋转函数 b相对a转
void rotate(PII& a, PII& b)
{
	//计算该向亮
    b.x -= a.x, b.y -= a.y;
    //由于是顺时针旋转90度，就把坐标带入进行计算
    int x = b.y, y = -b.x;
    //新的坐标加等于旧的坐标加上偏移量
    b.x = a.x + x, b.y = a.y + y;
}

int main()
{
    int n;
    cin >> n;

    int d = 0;
    while (n -- )
    {
        string str;
        cin >> str;
        int k = id[str.substr(0, 2)];
        char c = str[2];
        if (c != 'P')
        {
            int t = (d + turn[c]) % 4;
            p[k].x += dx[t], p[k].y += dy[t];
        }
        else
        {
            for (int i = 0; i < 4; i ++ )
            {
                if (i != k)
                    rotate(p[k], p[i]);                
            }
			//旋转后方向改变
            d = (d + 1) % 4;
        }
        
		//检查是否两只脚会踩在同一块地板上，如果有直接输出-1
        for (int i = 0; i < 4; i ++ )
            for (int j = 0; j < i; j ++ )
                if (p[i] == p[j])
                {
                    puts("-1");
                    return 0;
                }

        for (int i = 0; i < 4; i ++ )
        {
        	// 求出这个过程中最小最大的四个边界
            minx = min(minx, p[i].x);
            miny = min(miny, p[i].y);
            maxx = max(maxx, p[i].x);
            maxy = max(maxy, p[i].y);
        }
    }

    cout << (maxx - minx + 1) * (maxy - miny + 1) << endl;
    return 0;
}