一、多项式加法运算

1.1 多项式加法步骤

前面我们提到过多项式相加的一种基本思想，我们现在来简单回忆一下。我们有两个多项式：
$P1 = 3{x^5} + 4{x^4} - {x^3} + 2x - 1$
$P2 = 2{x^4} + {x^3} - 7{x^2} + x$
相加操作的步骤为：相同指数的项系数相加，其余部分进行拷贝。具体如下图所示：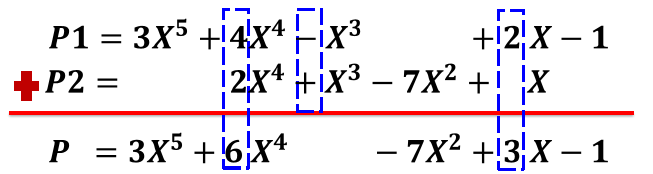
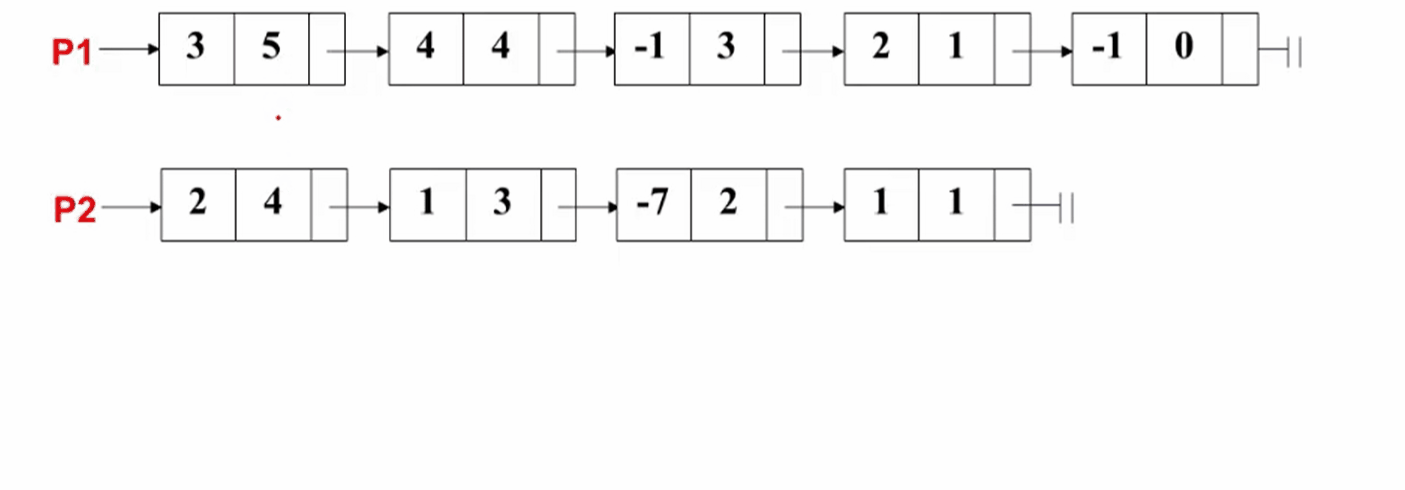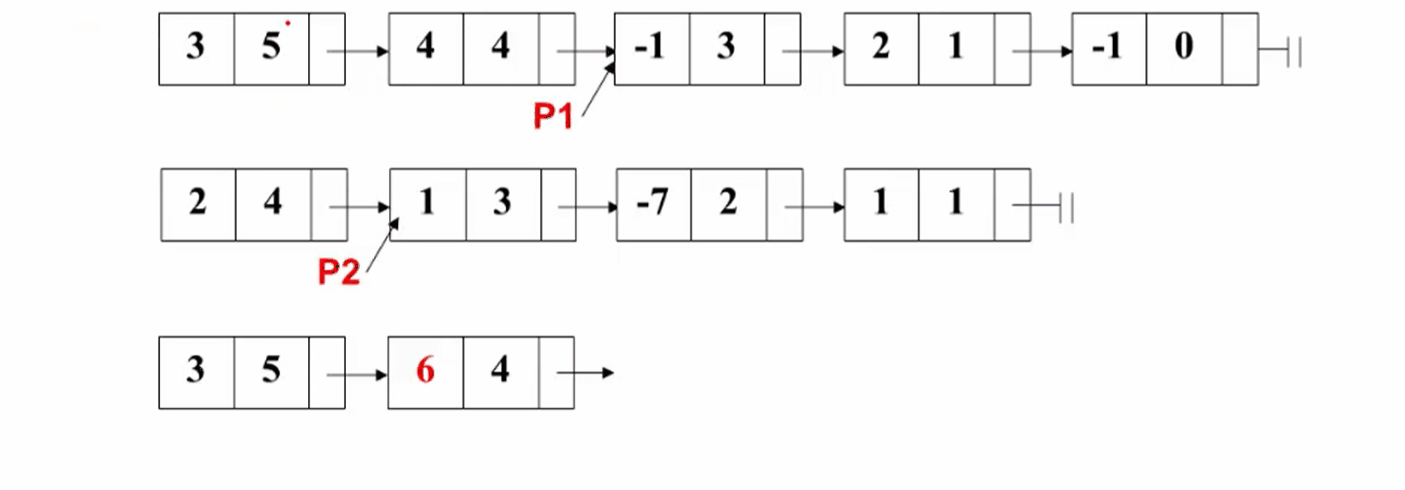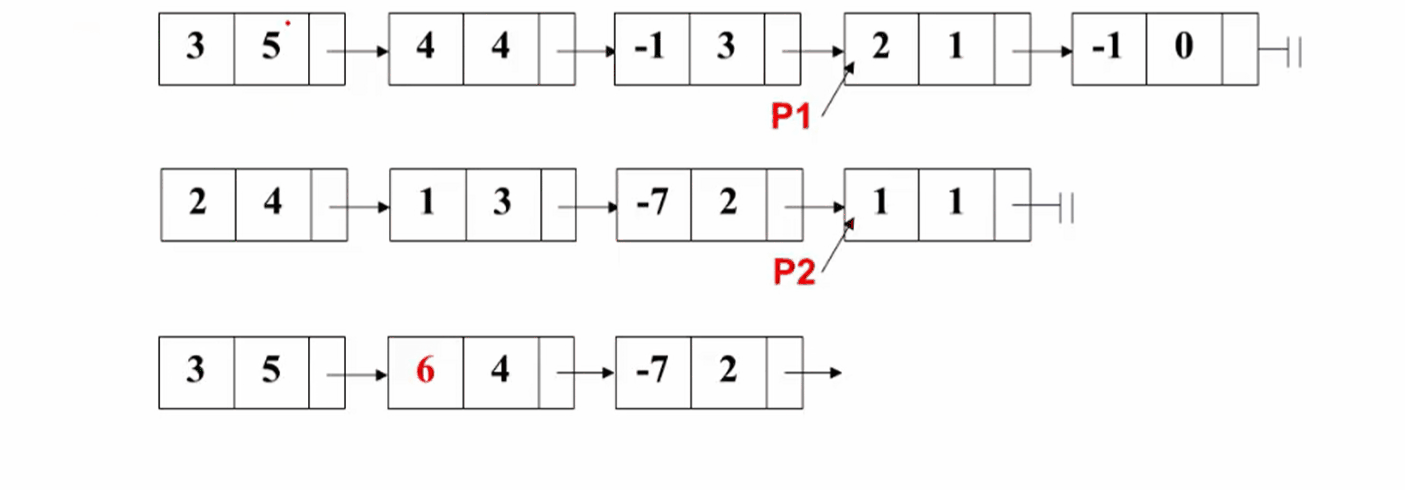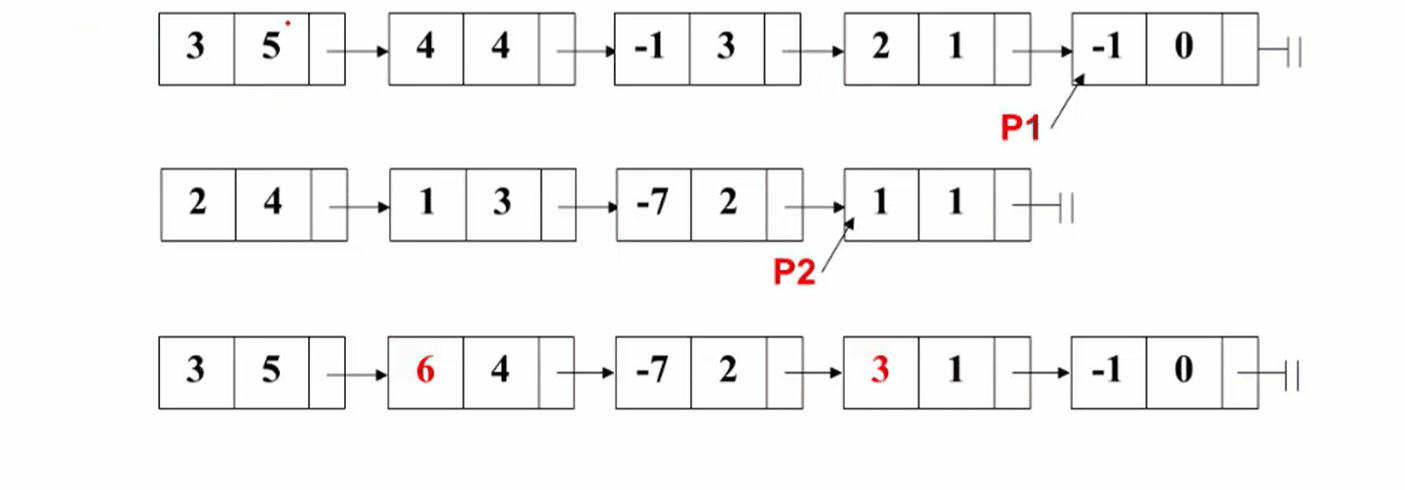
在这里插入图片描述

我们下面来讨论一下：多项式相加在我们计算机里怎么实现。我们可以采用一个不带头结点的单向链表来表示，如下图所示：
在这里插入图片描述
在这个表示里面我们可以看到：我们的每一项是对应这个单向链表的一个结点，这个结点就包含三个分量，一个是系数、一个是指数、一个是指向下一项的指针。所以每一项按照指数递降的顺序串在一起。

接下来我们来看一下它具体的数据结构：

struct PolyNode {
	int coef; // 系数
	int expon; // 指数
	struct PolyNode *link; // 指向下一个节点的指针
};
typedef struct PolyNode *Polynomial;
Polynomial P1, P2;

下面我们想把这两个多项式加在一起，我们的这种思路是这样的：

我们用P1、P2分别指向这两个多项式的第一个结点，也就是这两个多项式最高项，然后不断地循环。循环的过程是这样的：
①比较这两项的指数，根据指数大小关系执行相应操作，如下所示：
----P1->expon==P2->expon: 系数相加，若结果不为0，则作为结果多项式对应项的系数。同时，P1和P2都分别指向下一项；
----P1->expon>P2->expon: 将P1的当前项存入结果多项式，并使P1指向下一项；
----P1->expon<P2->expon: 将P2的当前项存入结果多项式，并使P2指向下一项；
②当某一多项式处理完时，将另一个多项式的所有结点依次复制到结果多项式中去。
对应的操作如下图所示：

1.2 多项式加法实现代码

步骤1：
我们设计一个函数，这个函数的参数是两个指针P1和P2，指向要相加的两个多项式。对于结果多项式来讲，我们最后要return回去的是这个相加后的单向链表的第一个结点，所以我们要记住结果多项式的头在哪里。因为我们不断地要把新的一项加到结果多项式的后面，所以我们也要知道结果多项式的尾巴在哪里。所以我们用两个指针front和rear分别指向结果多项式的头和尾。那么为了方便这个操作，我们构造一个临时的空结点暂时作为结果多项式的表头，font和rear都指向它。

Polynomial PolyAdd (Polynomial P1, Polynomial P2)
{
	Polynomial front, rear, temp;
	rear = (Polynomial) malloc(sizeof(struct PolyNode));
	front = rear; /* 由front 记录结果多项式链表头结点 */
	
	return front;
}

步骤2：
接下来进行循环，不断判别P1和P2是否为空。当两个多项式都不为空时，说明需要比较P1和P2对应项的指数，并根据比较结果进行相关操作。

Polynomial PolyAdd (Polynomial P1, Polynomial P2)
{
	Polynomial front, rear, temp;
	int sum;  //P1 P2当前项指数相等，则将系数加到sum中
	rear = (Polynomial) malloc(sizeof(struct PolyNode));
	front = rear;      /* 由front 记录结果多项式链表头结点 */
	while ( P1 && P2 ) /* 当两个多项式都有非零项待处理时 */
		//Compare函数比P1 P2指数大小。
		switch ( Compare(P1->expon, P2->expon) ) {

		case 1:     //返回1，说明P1指数大
			Attach( P1->coef, P1->expon, &rear);   //将P1当前这一项拷贝到结果多项式表尾rear后
			P1 = P1->link;   //P1往后挪
			break;

		case -1:    //返回-1，说明P2指数大
			Attach(P2->coef, P2->expon, &rear); //将P2当前这一项拷贝到结果多项式表尾rear后
			P2 = P2->link; //P2往后挪
			break;

		case 0:		//返回0，说明指数一样大
			sum = P1->coef + P2->coef; //记录这两项的系数
			if ( sum ) Attach(sum, P1->expon, &rear); //如果系数相加不为0，则接到rear后
			P1 = P1->link; //P1 P2都往后挪
			P2 = P2->link;
			break;
	}
	
	return front;

步骤3：
当循环结束后，说明P1和P2有一个空了。这时用两个for循环分别处理P1和P2不为空时将其接到rear后的操作。这两个循环做完后，做一些函数的扫尾工作：

Polynomial PolyAdd (Polynomial P1, Polynomial P2)
{
	Polynomial front, rear, temp;
	int sum;
	rear = (Polynomial) malloc(sizeof(struct PolyNode));
	front = rear; /* 由front 记录结果多项式链表头结点 */
	while ( P1 && P2 ) /* 当两个多项式都有非零项待处理时 */
		switch ( Compare(P1->expon, P2->expon) ) {
		case 1:
			Attach( P1->coef, P1->expon, &rear);
			P1 = P1->link;
			break;
		case -1:
			Attach(P2->coef, P2->expon, &rear);
			P2 = P2->link;
			break;
	case 0:
			sum = P1->coef + P2->coef;
			if ( sum ) Attach(sum, P1->expon, &rear);
			P1 = P1->link;
			P2 = P2->link;
			break;
	}
	/* 将未处理完的另一个多项式的所有节点依次复制到结果多项式中去 */
	for ( ; P1; P1 = P1->link ) Attach(P1->coef, P1->expon, &rear);
	for ( ; P2; P2 = P2->link ) Attach(P2->coef, P2->expon, &rear);
	rear->link = NULL;
	temp = front;
	front = front->link; /*令front指向结果多项式第一个非零项 */
	free(temp); /* 释放临时空表头结点 */
	return front;
}

最后我们来看看Attach函数怎么实现的：

void Attach( int c, int e, Polynomial *pRear )
{ /* 由于在本函数中需要改变当前结果表达式尾项指针的值， */
/* 所以函数传递进来的是结点指针的地址，*pRear指向尾项*/
	Polynomial P;
	P =(Polynomial)malloc(sizeof(struct PolyNode)); /* 申请新结点 */
	P->coef = c; /* 对新结点赋值 */
	P->expon = e;
	P->link=NULL;
	/* 将P指向的新结点插入到当前结果表达式尾项的后面 */
	(*pRear)->link = P;
	*pRear = P; /* 修改pRear值 */
}

流程如下图所示：
在这里插入图片描述

二、整体代码

#include <stdio.h>
#include <stdlib.h>

struct PolyNode
{
	int coef;
	int expon;
	struct PolyNode *link;
};
typedef struct PolyNode *Polynomical;


int Compare(int a, int b)
{
	return a > b ? 1 : b > a ? -1 : 0;
}

void Attach(int c, int e, Polynomical *pRear)
{
	Polynomical P;
	P = (Polynomical)malloc(sizeof(struct PolyNode));
	P->coef = c;
	P->expon = e;
	P->link = NULL;
	(*pRear)->link = P;
	*pRear = P;
}

Polynomical PolyAdd(Polynomical P1, Polynomical P2)
{
	Polynomical front, rear, temp;
	int sum;
	rear = (Polynomical)malloc(sizeof(struct PolyNode));
	front = rear;
	while (P1 && P2) {
		switch (Compare(P1->expon, P2->expon)) {

		case 1:
			Attach(P1->coef, P1->expon, &rear);
			P1 = P1->link;
			break;
		case -1:
			Attach(P2->coef, P2->expon, &rear);
			P2 = P2->link;
			break;
		case 0:
			sum = P1->coef + P2->coef;
			if(sum)
				Attach(sum, P1->expon, &rear);
			P1 = P1->link;
			P2 = P2->link;
			break;
		}
	}
	for (; P1; P1 = P1->link) Attach(P1->coef, P1->expon, &rear);
	for (; P2; P2 = P2->link) Attach(P2->coef, P2->expon, &rear);
	rear->link = NULL;
	temp = front;
	front = front->link;
	free(temp);

	return front;
}

int main(void)
{
	int coef1[5] = {3, 4, -1, 2, -1};
	int expon1[5] = {5, 4, 3, 1, 0};
	int coef2[4] = {2, 1, -7, 1};
	int expon2[4] = {4, 3, 2, 1};

	Polynomical P1 = (Polynomical)malloc(sizeof(struct PolyNode));
	Polynomical P2 = (Polynomical)malloc(sizeof(struct PolyNode));
	P1->link = NULL;
	P2->link = NULL;
	Polynomical P1_temp = P1;
	Polynomical P2_temp = P2;

	for (int i = 0; i < 5; i++)
	{
		Attach(coef1[i], expon1[i], &P1_temp);
	}
	P1 = P1->link;

	for (int j = 0; j < 4; j++)
	{
		Attach(coef2[j], expon2[j], &P2_temp);
	}
	P2 = P2->link;

	Polynomical P3 = PolyAdd(P1, P2);

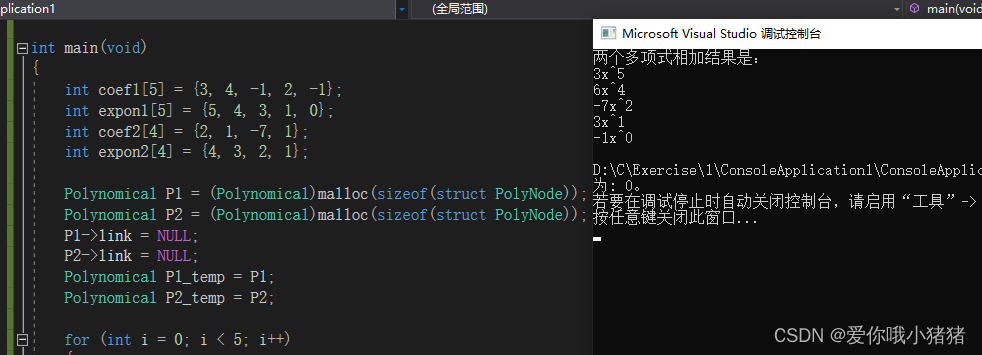
	printf("两个多项式相加结果是：\n");
	while (P3 != NULL)
	{
		printf("%dx^%d\n", P3->coef, P3->expon);
		P3 = P3->link;
	}

	return 0;
}

运行，结果如下，正确。
在这里插入图片描述

原文链接：https://blog.csdn.net/InnerPeaceHQ/article/details/121989856