运动估计算法的程序实现_光流法--Lucas Kanade算法

一 光流简介:

光流问题涉及尝试找出一幅图像中的许多点在第二幅图像中移动的位置--通常是以视频序列完成的，因此可以假定第一幅图像中的大部分点框架都可以在第二幅图像中找到。光流可以用于场景中物体的运动估计，设置用于相机相对于整个场景的自运动估计。光流算法的理想输出是两帧图像中每个像素的速度的估计关联，或者等效的，一幅图像中每个像素的位移矢量，指示该像素在另一幅图像中的相对位置，如果图像中的每个像素都采用这种方法通常称为“稠密光流”。还有一种算法称为“稀疏光流”，仅仅只跟踪图像中某些点的子集，该算法通常是快速且可靠的，因为其将注意力只放在容易跟踪的特定点上，稀疏跟踪的计算成本远远低于稠密跟踪，这也导致了后者的研究基本被限制在了学术圈。

二 Lucas Kanade稀疏光流算法:

2.1 简要介绍

Bruce D. Lucas 和 Takeo Kanade在1981年提出了Lucas Kanade（LK）算法试图计算稠密光流。然而该方法容易应用到输入图像中的点的子集，所以反而成为了稀疏光流算法的重要技术，该算法可以应用到稀疏场景中，因为它仅依赖于围绕某个兴趣点的一些小窗口导出的局部信息，但该算法的缺点在于，如果像素点的运动幅度过大，运动到了局部窗口之外，那么算法将无法找到。这个问题就导致了“金字塔-LK算法的发展”，该算法从图像金字塔的最低细节开始跟踪，并逐渐跟踪至更精细的细节。跟踪图像金字塔允许大幅度的运动被局部窗口捕捉。

2.2 工作原理

LK算法是一种两帧差分的光流估计算法，其基本思想基于以下三个假设。

• 亮度恒定：场景中目标图像的像素看起来在帧到帧移动是不发生改变。对于灰度图像（对于彩色图像同适用）这意味着像素的灰度值不会随着帧的跟踪改变。
• 时间持续性（微小移动）：图像上相机的移动随时间变化缓慢。实际上，这意味着时间的变化不会引起像素位置的剧烈变化，这样像素的灰度值才能对位置求对应的偏导数。
• 空间一致性：场景中相同表面的相邻点具有相似的运动，并且其投影到图像平面上的距离也比较近。

三个基本假设中前两个是光流法的基本假设，第三个是LK算法特有的。

基于前两个假设，我们得到图像的约束方程：

其中

是

时刻图像在

位置的亮度。

利用泰勒公式对函数

在

处展开可得：

其中

为泰勒公式的高阶余项近似为0。

联立公式(1)和(2)可以得到

等价为

其中

和

分别为像素点沿着x和y方向的导数，沿x和y方向的速度分量分别记为

和

，可以将以上式子简写为：

进一步简化为矩阵形式：

由于以上的方程有

和

两个未知数，所以无法求解，那们我们就要基于第三条假设得到一些其他的方程进行联立求解。

回到第三条假设，我和可以假设在一个大小为

的窗口内，图像的光流是一个恒定值。那么就可以得到以下方程组：

为了求解以上过度约束的系统可以采用最小二乘法对以上的方程还是进行最小化，将以上方程采用矩阵形式进行表示：

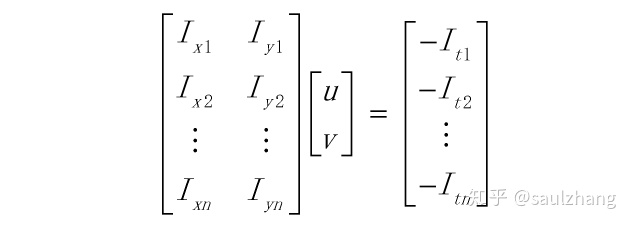
记做

,采用最小二乘法得到

则最终所有求解的光流（速度矢量）为：

矩阵形式表示如下：

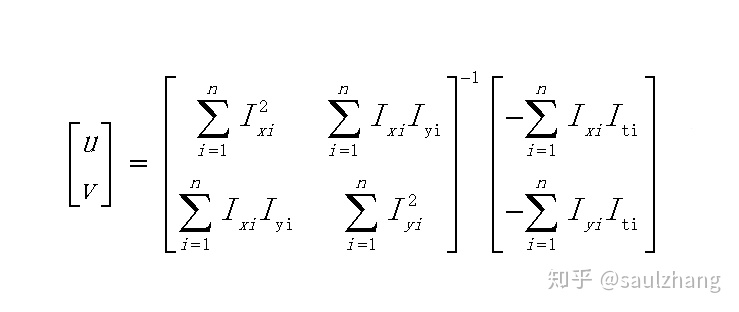
最终求得

便是LK算法所对应的光流。

2.3 代码实现

以下为python-opencv的官方实现：

import 

实验效果：