棋盘覆盖

最近算法oj作业
参考代码。我以16*16的方格为例子，一步一步来。期望能够共同进步！
原理什么的，可以看其他文章。

一、问题描述

题目描述
在一个2^k * 2^k 个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

输入要求
输入一个整数k，k<=5；
输入特殊格子的坐标x，y。

输出要求
输出一个由数值表示的二维矩阵。填充规则如下：
（1）用数值填充方格；
（2）特殊方格数值为0；
（3）从中心点开始；然后左上、右上、左下、右下的计数顺序填数；同一块用相同数值表示；
（4）每个数值占4个位置空间；右对齐，左补空格。

输入样例
3
1 2

输出样例
3 3 4 4 8 8 9 9
3 2 0 4 8 7 7 9
5 2 2 6 10 10 7 11
5 5 6 6 1 10 11 11
13 13 14 1 1 18 19 19
13 12 14 14 18 18 17 19
15 12 12 16 20 17 17 21
15 15 16 16 20 20 21 21

二、详细解析

1.首先假设特殊格子在（5，5）点。

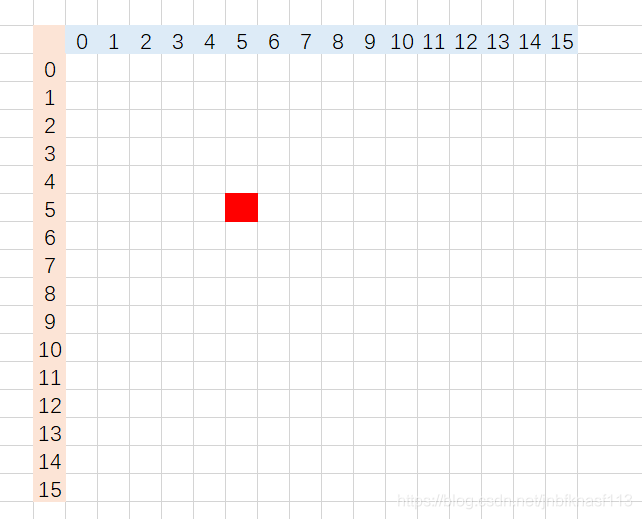
2.第一步能就是将其分为4部分，其实也就是16/2*16/2的方格，就可以得到。

如图中红线所示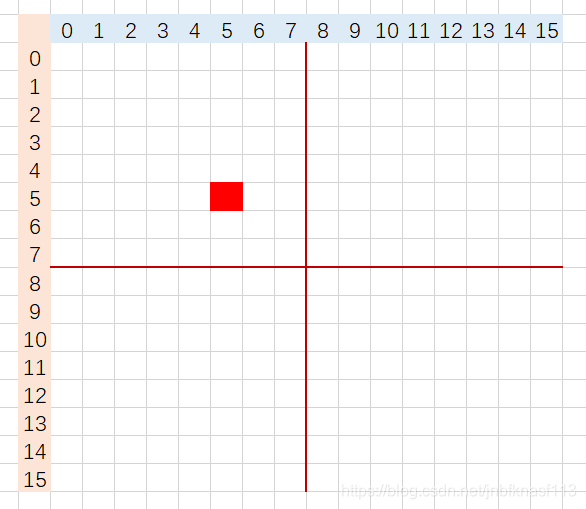

3.关键的来了！再分为四部分之后，查看这四部分是否还有特殊子。没有的分别加上，让其含有，然后再划分子问题。以这个为例子，右上，左下，右下没有，那么分别再他们的对角加上。

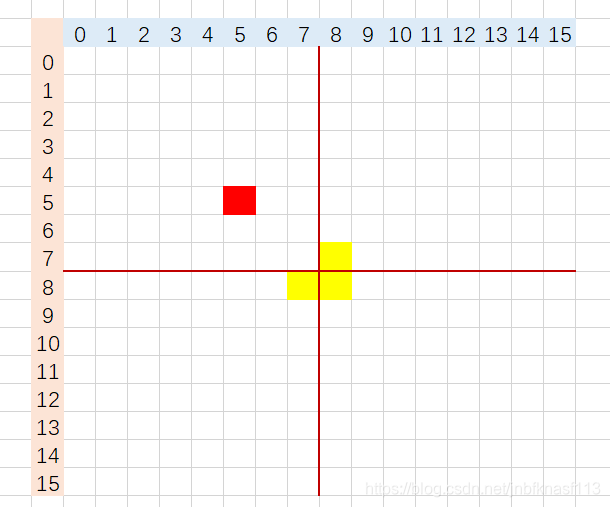
5.这样四个部分 分别含有特殊子，四个部分递归，进行问题分解。

如图中蓝线所示。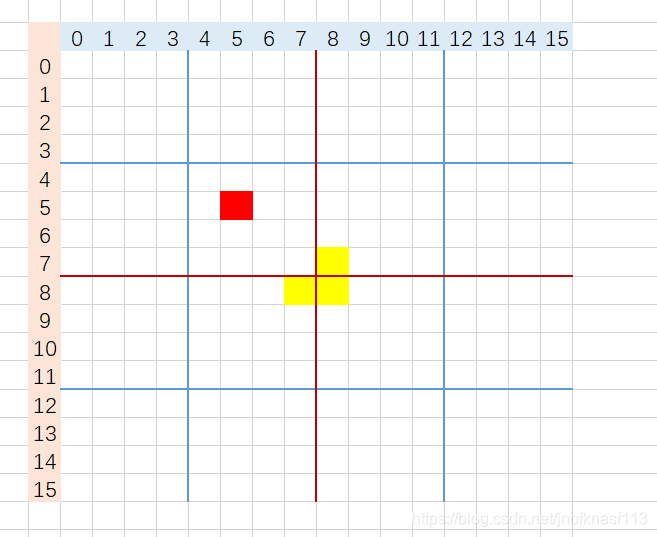

继续。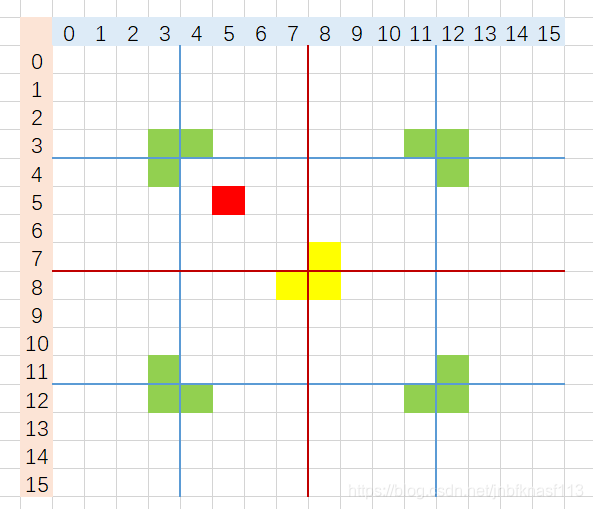

6.以左上部分为例子，递归求解 分成了四部分，不含有特殊的对角加上，继续对这左上的四部分递归。

如橙色线所示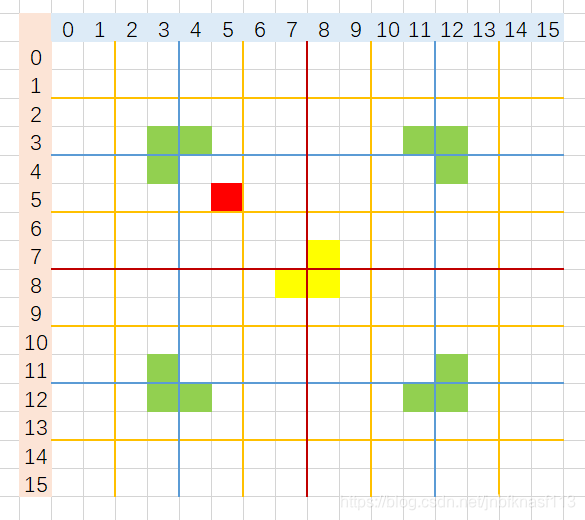


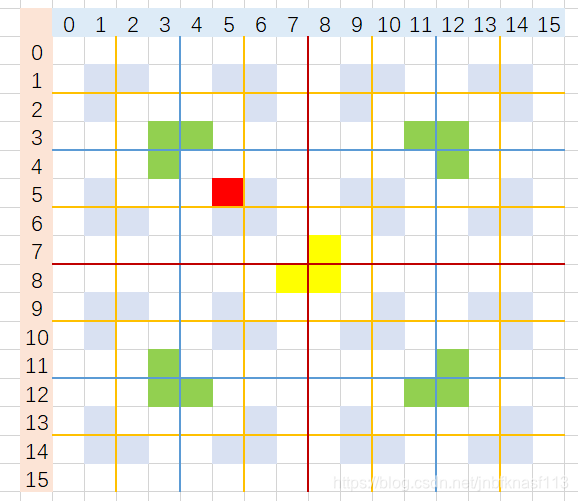
7.最后橙色线的格子里都含有特殊子了，那么都填充起来就OK了。

三、代码实现

代码：

#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
int number=0;
int Board[33][33];
//tr,tc是方格左上角的位置，dr,dc是特殊方格的位置
void ChessBoard(int tr,int tc,int dr,int dc,int size)
{
    if(size==1)
        return;
    int ind=++number;//骨牌的编号
    int s=size/2;//将棋盘分割为4个子问题,即行和列各取一半

    if(dr<tr+s && dc<tc+s)//当特殊格子在左上的子问题中
        ChessBoard(tr,tc,dr,dc,s);
    else//如果特殊格子不在左上时，将左上的右下角标记为黑格
    {
        Board[tr+s-1][tc+s-1]=ind;//用编号为ind的骨牌覆盖该子问题中的右下角
        ChessBoard(tr,tc,tr+s-1,tc+s-1,s);//继续覆盖其余格子
    }

    if(dr<tr+s && dc>=tc+s)//当特殊格子在右上的子问题中
        ChessBoard(tr,tc+s,dr,dc,s);
    else//如果特殊格子不在右上，将右上的左下角标记为黑格
    {
        Board[tr+s-1][tc+s]=ind;
        ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
    }

    if(dr>=tr+s && dc<tc+s)//当特殊格子在左下的子问题中
        ChessBoard(tr+s,tc,dr,dc,s);
    else//如果特殊格子不在左下时，将左下的右上角标记为黑格
    {
        Board[tr+s][tc+s-1]=ind;
        ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
    }

    if(dr>=tr+s && dc>=tc+s)//当特殊格子在右下的子问题中
        ChessBoard(tr+s,tc+s,dr,dc,s);
    else//如果特殊格子不在右下时，将右下的左上角标记为黑格
    {
        Board[tr+s][tc+s]=ind;
        ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
    }

}
int main()
{
    int k,x,y;
    scanf("%d",&k);
    int size=pow(2,k);
    scanf("%d%d",&x,&y);
    ChessBoard(0,0,x,y,size);
    for(int i=0;i<size;i++)
        {
            for(int j=0;j<size;j++)
            {
                printf("%4d",Board[i][j]);
            }
            printf("\n");
        }
    return 0;
}