11堆排序

https://blog.csdn.net/weixin_45796387/article/details/114994648?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162509768116780274190983%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=162509768116780274190983&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_alltop_positive~default-1-114994648.first_rank_v2_pc_rank_v29&utm_term=%E4%BA%8C%E5%8F%89%E6%A0%91&spm=1018.2226.3001.4187

————————二叉树详解

堆排序

1.简介

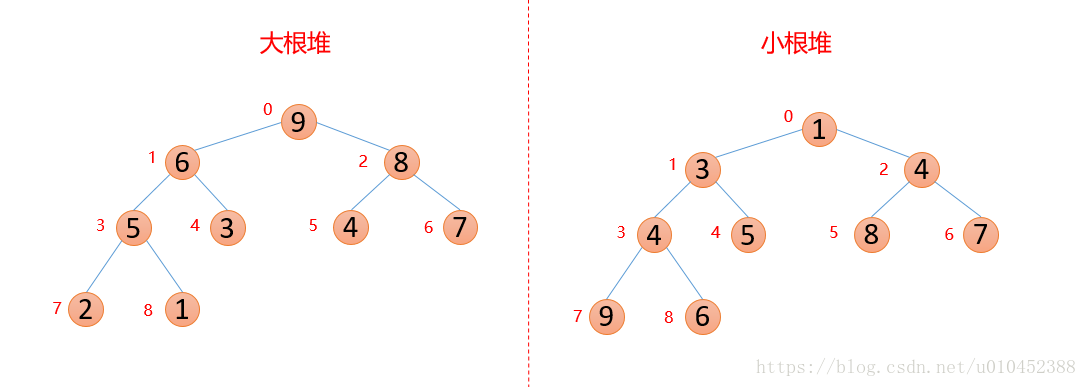
堆的结构可以分为大根堆和小根堆，是一个完全二叉树，而堆排序是根据堆的这种数据结构设计的一种排序，下面先来看看什么是大根堆和小根堆

条件：

1.首先是一个完全二叉树

2.父节点的值大于子节点

2.大根堆和小根堆

性质：每个结点的值都大于其左孩子和右孩子结点的值，称之为大根堆；每个结点的值都小于其左孩子和右孩子结点的值，称之为小根堆。

​ 我们对上面的图中每个数都进行了标记，上面的结构映射成数组就变成了下面这个样子。

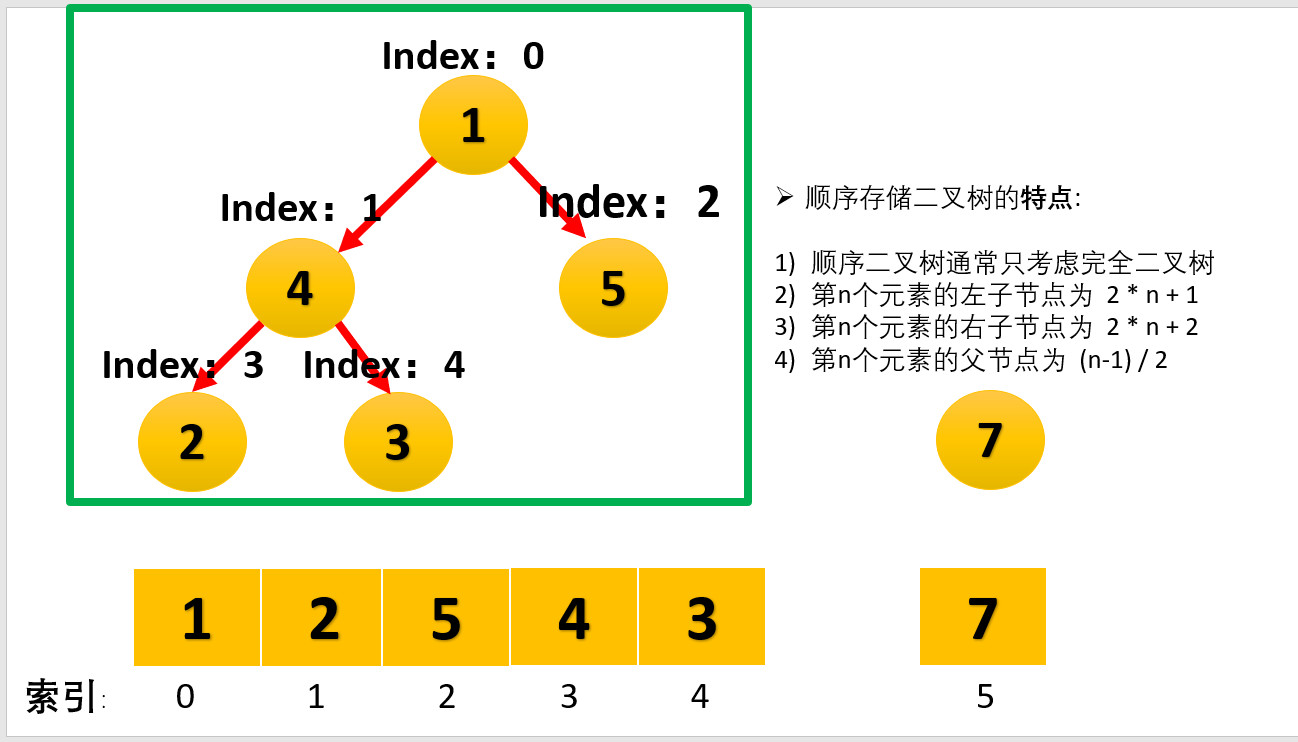
还有一个基本概念：查找数组中某个数的父结点和左右孩子结点，比如已知索引为****i****的数，那么。

1.parent: (i - 1) / 2;

2.child1: 2**i*+1

3.child2: 2**i*+2

3.大堆排序

基本思想：

​ 1.首先将待排序的数组构造成一个大根堆，此时，整个数组的最大值就是堆结构的顶端

​ 2.将顶端的数与末尾的数交换，此时，末尾的数为最大值，剩余待排序数组个数为n-1

​ 3.将剩余的n-1个数再构造成大根堆，再将顶端数与n-1位置的数交换，如此反复执行，便能得到有序数组

4.实现步骤

1.大根堆

思路：从0 到n个节点都需要做一次小堆，三个数进行比较，取最大值，放到三个数顶端，三个数的顶端需要和parent节点比较，直到小于等于0时释放.

void swap(int arr[], int i, int j)
{
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

void buildHeap(int tree[], int max)
{
    int parent = (max - 1) / 2;
    if (parent < 0)//注意是小于0时,不进行了,此时parent没有数据
    {
        return;
    }
    //如果parent节点有，则比较
    if (tree[max] <= tree[parent])
    {
        return; //代表parent节点大，无需交换
    }
    else
    {
        //代表parent节点小，交换
        swap(tree, max, parent);//交换
        buildHeap(tree, parent);//再次与上一个parent节点比较
    }
}

//最小堆排序
void heapify(int tree[], int n, int i)
{
    if (i >= n)
    {
        return;
    }
    int c1 = 2 * i + 1;
    int c2 = 2 * i + 2;
    int max = i;
    if (c1 < n && tree[c1] > tree[max])
    {
        max = c1;
    }
    if (c2 < n && tree[c2] > tree[max])
    {
        max = c2;
    }
    if (max != i)
    {
        //进行交换
        swap(tree, max, i);
        //需要跟parent进行比较，根据公式parent = (i - 1) / 2;
        buildHeap(tree, i);//与上一节点比较
    }
    heapify(tree, n, i + 1);
}

2.每次末尾的数与第一个数交换

void heap_sort(int tree[], int n)
{
    heapify(tree, n, 0); //进行大顶堆
    //最后一个数与第一个元素交换
    for (int i = n - 1; i > 0; --i)
    {
        swap(tree, i, 0); //末尾的和第一个元素交换
        heapify(tree, i, 0);
    }
}

int main(int argc, char const *argv[])
{
    int tree[] = {3, 10, 5, 8, 1, 7, 6, 9, 2, 100, 200, 120, 11, 30};
    int length = sizeof(tree) / sizeof(tree[0]);
    heap_sort(tree, length);
    for (int i = 0; i < length; i++)
    {
        printf("%d\n", *(tree + i));
    }
    system("pause");
    return 0;
}

3.堆排序的事件复杂度

nlgn：

4.堆应用场景

从10万个数里面选出最小的10个”为例，利用堆排序从无序数组里面选择最大（小）的部分元素。

实现原理：用个无序数组模拟10万个数，取无序数组里面前面的10个数字构建一个大顶堆，从第11个数开始逐个与堆顶元素进行比较，小于堆顶元素则入堆，并重新构建大顶堆，这样能保证堆顶元素始终是最大的。循环完毕之后，堆里面的10个元素就是最小的了。

如果采用堆来实现，则非常容易取到值，取最大元素。

第一次堆：大顶堆堆顶就是最大值，n次

第二次堆：先把顶端元素与最后的元素交换。再次进行大顶堆

第三次堆:…

也就是，需要的次数非常快。

5.总结使用场景

• 1.适合从无序的数据中，取出部分数据，比如最大的十个数，或者最小的十个数

• 2.适合大量的数据