根据树的叶子结点个数、非叶子节点个数、树的深度等等,推导出的公式、定理也有不少,可以自己手工推算一下,记忆会更深刻,此博文只介绍公式、定理内容,不作推导。
1. 二叉树第i层上至多有2^i-1个结点,其中i大于等于1,2^i表示2的i次方;
2. 深度为k的二叉树至多有2^k-1个结点,其中k大于等于1;
3. 任何一颗非空二叉树,若它的叶子结点数为m,2度结点数为n,则m=n+1;
4. 具有n个结点的完全二叉树深度为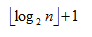
5. 设完全二叉树中结点编号依次为1到n:
i=1: 无双亲;
i不等于1:双亲编号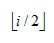
2i>n:无左孩子,否则左孩子为2i;
2i+1>n:无右孩子,否则有孩子为2i+1.
6. 二叉树不是树的特殊情形,而是与树不同的数据结构,即二叉树并不等价于2度的树;
完全二叉树的存储:将所有结点按层次次序存储在一组地址连续的存储单元中;
非完全二叉树的存储:先扩充为完全二叉树,再按完全二叉树存之。
7. 折半查找判定树是任一结点的左、右子树上的结点数最多相差一的二叉树,除最下面一层外,各层结点数均达到最大值。
8. 二叉排序树:左孩子的值<根的值<右孩子的值,新节点作为二叉排序树的叶子。
9. 平衡二叉树(AVL树):任何结点的左子树和右子树的高度最多相差一的二叉排序树。
平衡因子:-1,0,1.
10. 几个例子
(1)设一个二叉树有3个叶子结点,8个度为1的结点,则共有结点(13)个。
分析:定理 任一非空二叉树结点总数为:n=n0+n1+n2 (n0、n1、n2分别为度为0、1、2的结点个数),
分支总数为b=n1+n2
b=n-1=n0+n1+n2-1
所以 n2=n0-1
结点数为 3+2+8=13
(2)设一棵完全二叉树共699个结点,则叶子结点数为(350)。
分析:2^10>699>2^9-1 可见共10层,9层全满(2^9-1=511)
第10层有 699-511=188个叶子结点
2^(9-1)-188/2=162个叶子结点在第9层,共188+162=350个叶子结点。