前趋图(Precedence Graph):是一个有向无循环图,记为DAG(Directed Acyclic Graph),前趋图中必须不存在循环, 该图通常用于 表现事务之间先后顺序的制约关系 。
结点:可以表示一个语句、一个程序段或是一个进程,
有向边: 结点间的有向边表示两个结点之间存在的前趋关系。
程序顺序执行 特性
- 顺序性
- 封闭性:即程序运行时独占全机资源
- 可再现性
程序并发执行特性
- 间断性
- 失去封闭性:是多个程序共享系统中的各种资源
- 不可再现性
在计算机中,经常采用流水线方式执行指令,每一条指令都可以分解为取指、分析 和执行三步。
- 〇 表示一个程序、进程或是语句的结点。
- → 表示结点间的执行顺序。
前趋关系"→"的形式化描述:→ ={Ai, Bi, Ci} 取指操作为 Ai,分析操作为 Bi 和执行操作为 Ci(i=1,2,3)。
如图所示为三个任务各程序段并发执行的前驱图。
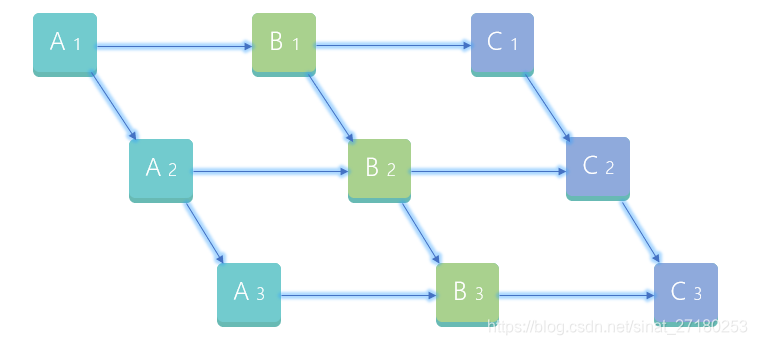
开始结点 ( Initial Node ):A1 没有前趋结点,不受任何制约,可以直接执行
终止结点 ( Final Node ): C3 没有后继结点
直接前驱: Bi开始执行之前Ai必须完成, 此时称 Ai 是 Bi 的 直接前驱
直 接后继: Bi开始执行之前Ai必须完成, 此时称 Bi 是 Ai 的 直接前驱
重量( Weight ) : 用于表示该结点所含有的程序量或程序的执行时间
在前趋图中, 执行先后顺序的制约关系 可分为两种: 直接制约 和 间接制约 。
直接制约: 同操作中 , 多个步骤之间 的制约关系,也可以说是“同步的进程之间的制约关系”。 如图 A1、B1、C1 是一条指令的取指、分析、执行的三个步骤,所以它们之间的关系是直接制约。
间接制约: 多个操作之间 , 相同步骤 的制约关系,也可以说是“互斥的进程之间的制约关系”。 如图A1、A2、A3 之间就存在间接制约的关系。
并行执行: B1、A2,
C1、B2、A3,
C2、B3,
版权声明:本文为sinat_27180253原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。