数据挖掘十大经典算法之K-means

数据挖掘十大经典算法之K-means

引言：k-means与kNN虽然都是以k打头，但却是两类算法——kNN为监督学习中的分类算法，而k-means则是非监督学习中的聚类算法；二者相同之处：均利用近邻信息来标注类别。
聚类是数据挖掘中一种非常重要的学习流派，指将未标注的样本数据中相似的分为同一类，正所谓“物以类聚，人以群分”嘛。k-means是聚类算法中最为简单、高效的，核心思想：由用户指定k个初始质心（initial centroids)，以作为聚类的类别（cluster），重复迭代直至算法收敛。
在k-means算法中，用质心来表示cluster；且容易证明k-means算法收敛等同于所有质心不再发生变化。基本的k-means算法流程如下：

选取k个初始质心（作为初始cluster）；
repeat：
对每个样本点，计算得到距其最近的质心，将其类别标为该质心所对应的cluster；
重新计算k个cluser对应的质心；
until 质心不再发生变化
对于欧式空间的样本数据，以平方误差和（sum of the squared error, SSE)作为聚类的目标函数，同时也可以衡量不同聚类结果好坏的指标：
SSE=∑i=1k∑x∈Cidist(x,ci)
表示样本点x到cluster Ci 的质心 ci 距离平方和；最优的聚类结果应使得SSE达到最小值。

# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt


def loadDataSet(fileName):
    '''
    加载测试数据集，返回一个列表，列表的元素是一个坐标
    '''
    dataList = []
    with open(fileName) as fr:
        for line in fr.readlines():
            curLine = line.strip().split('\t')
            fltLine = list(map(float, curLine))
            dataList.append(fltLine)
    return dataList


def randCent(dataSet, k):
    '''
    随机生成k个初始的质心
    '''
    n = np.shape(dataSet)[1]  # n表示数据集的维度
    centroids = np.mat(np.zeros((k, n)))
    for j in range(n):
        minJ = min(dataSet[:, j])
        rangeJ = float(max(dataSet[:, j]) - minJ)
        centroids[:, j] = np.mat(minJ + rangeJ * np.random.rand(k, 1))
    return centroids


def kMeans(dataSet, k):
    '''
    KMeans算法，返回最终的质心坐标和每个点所在的簇
    '''
    m = np.shape(dataSet)[0]  # m表示数据集的长度（个数）
    clusterAssment = np.mat(np.zeros((m, 2)))

    centroids = randCent(dataSet, k)  # 保存k个初始质心的坐标
    clusterChanged = True
    iterIndex = 1  # 迭代次数
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            minDist = np.inf;
            minIndex = -1
            for j in range(k):
                distJI = np.linalg.norm(np.array(centroids[j, :]) - np.array(dataSet[i, :]))
                if distJI < minDist:
                    minDist = distJI;
                    minIndex = j
            if clusterAssment[i, 0] != minIndex: clusterChanged = True
            clusterAssment[i, :] = minIndex, minDist ** 2
            print("第%d次迭代后%d个质心的坐标:\n%s" % (iterIndex, k, centroids))  # 第一次迭代的质心坐标就是初始的质心坐标
            iterIndex += 1
        for cent in range(k):
            ptsInClust = dataSet[np.nonzero(clusterAssment[:, 0].A == cent)[0]]  # get all the point in this cluster

            centroids[cent, :] = np.mean(ptsInClust, axis=0)
    return centroids, clusterAssment


def showCluster(dataSet, k, centroids, clusterAssment):
    '''
    数据可视化,只能画二维的图（若是三维的坐标图则直接返回1）
    '''
    numSamples, dim = dataSet.shape
    if dim != 2:
        return 1

    mark = ['or', 'ob', 'og', 'ok', 'oy', 'om', 'oc', '^r', '+r', 'sr', 'dr', '<r', 'pr']

    # draw all samples
    for i in range(numSamples):
        markIndex = int(clusterAssment[i, 0])
        plt.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])

    mark = ['Pr', 'Pb', 'Pg', 'Pk', 'Py', 'Pm', 'Pc', '^b', '+b', 'sb', 'db', '<b', 'pb']
    # draw the centroids
    for i in range(k):
        plt.plot(centroids[i, 0], centroids[i, 1], mark[i], markersize=12)

    plt.show()


if __name__ == '__main__':
    dataMat = np.mat(loadDataSet('./testSet'))  # mat是numpy中的函数，将列表转化成矩阵
    k = 4  # 选定k值，也就是簇的个数（可以指定为其他数）
    cent, clust = kMeans(dataMat, k)
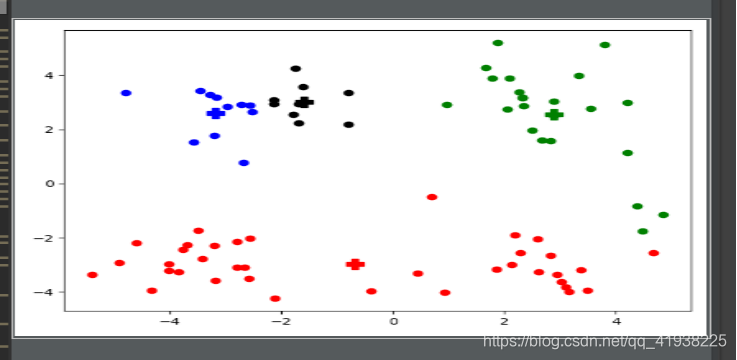
    showCluster(dataMat, k, cent, clust)

实验结果：