下文主要围绕以下问题展开:
- 施密特正交化的物理意义
- 特征子空间的含义
- 如何理解“实对称矩阵只用对同一特征值对应的特征向量进行正交化”(重点!)
施密特正交化的物理意义
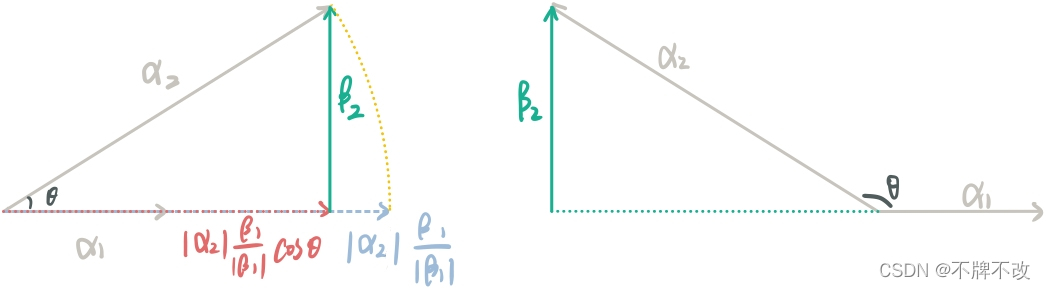
施密特正交化的过程:
对 α 1 \alpha_1α1 和 α 2 \alpha_2α2 进行施密特正交化(下简称为”正交化“)
- β 1 = α 1 \beta_1 = \alpha_1β1=α1
- β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_2 = \alpha_2 - \frac{(\alpha_2, \beta_1)}{(\beta_1,\beta_1)}\beta_1β2=α2−(β1,β1)(α2,β1)β1
整体上理解一下,( α 2 , β 1 ) (\alpha_2, \beta_1)(α2,β1) 表示 α 2 \alpha_2α2 和 β 1 \beta_1β1 的内积,是一个数;同样地,( β 1 , β 1 ) (\beta_1,\beta_1)(β1,β1) 也是一个数;β 1 \beta_1β1 就是 α 1 \alpha_1α1。
所以 β 2 \beta_2β2 本质上就是 α 1 \alpha_1α1 和 α 2 \alpha_2α2 的线性组合。
化简一下 β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 \beta_2 = \alpha_2 - \frac{(\alpha_2, \beta_1)}{(\beta_1,\beta_1)}\beta_1β2=α2−(β1,β1)(α2,β1)β1 :
β 2 = α 2 − ( α 2 , β 1 ) ( β 1 , β 1 ) β 1 = α 2 − ∣ α 2 ∣ ∣ β 1 ∣ c o s θ ∣ β 1 ∣ 2 β 1 = α 2 − ∣ α 2 ∣ c o s θ ∣ β 1 ∣ β 1 = α 2 − ∣ α 2 ∣ β 1 ∣ β 1 ∣ c o s θ \beta_2 = \alpha_2 - \frac{(\alpha_2, \beta_1)}{(\beta_1,\beta_1)}\beta_1 \\ =\alpha_2 - \frac{|\alpha_2||\beta_1|cos\theta}{|\beta_1|^2}\beta_1 \\ = \alpha_2 - \frac{|\alpha_2|cos\theta}{|\beta_1|}\beta_1 \\ = \alpha_2 - |\alpha_2|\frac{\beta_1}{|\beta_1|}cos\thetaβ2=α2−(β1,β1)(α2,β1)β1=α2−∣β1∣2∣α2∣∣β1∣cosθβ1=α2−∣β1∣∣α2∣cosθβ1=α2−∣α2∣∣β1∣β1cosθ
其中 θ \thetaθ 为 α 1 \alpha_1α1 和 α 2 \alpha_2α2 的夹角。
可视化后:
特征子空间的含义
简单理解:对于一个矩阵 A AA 的一个特征值 λ \lambdaλ ,该特征值对应的线性无关的特征向量为 α 1 \alpha_1α1 、 α 2 \alpha_2α2 、 …… 、α s \alpha_sαs,这 s ss 个线性无关的特征向量线性组合能构成的全部向量与零向量构成的集合称为 A AA 的特征值 λ \lambdaλ 的特征子空间。
严谨定义:
给定 n nn 阶矩阵 A AA ,规定 V λ = { α ∈ C n ∣ A α = λ α } V_\lambda = \{\alpha∈C^n|A\alpha=\lambda \alpha\}Vλ={α∈Cn∣Aα=λα}
(1)V λ V_\lambdaVλ 非空:0 ∈ V λ 0 ∈ V_\lambda0∈Vλ
(2)V λ V_\lambdaVλ 对加法封闭:
α , β ∈ V λ ⇒ A α = λ α , A β = λ β ⇒ A ( α + β ) = λ ( α + β ) ⇒ α + β ∈ V λ \alpha,\beta∈V_\lambda \\ \Rightarrow A\alpha=\lambda\alpha,A\beta=\lambda\beta \\ \Rightarrow A(\alpha+\beta)=\lambda(\alpha+\beta) \\ \Rightarrow \alpha+\beta∈V_\lambdaα,β∈Vλ⇒Aα=λα,Aβ=λβ⇒A(α+β)=λ(α+β)⇒α+β∈Vλ
(3)V λ V_\lambdaVλ 对数乘封闭:
α ∈ V λ ⇒ A α = λ α ⇒ A ( k α ) = k ( A α ) = k ( λ α ) = λ ( k α ) ⇒ k α ∈ V λ \alpha∈V_\lambda \\ \Rightarrow A\alpha=\lambda\alpha\\ \Rightarrow A(k\alpha)=k(A\alpha)=k(\lambda\alpha) = \lambda(k\alpha) \\ \Rightarrow k\alpha∈ V_\lambdaα∈Vλ⇒Aα=λα⇒A(kα)=k(Aα)=k(λα)=λ(kα)⇒kα∈Vλ
(4)α 1 , α 2 , . . . , α s ∈ V λ ⇒ k 1 α 1 + k 2 α 2 + . . . + k s α s ∈ V λ , k i ∈ C \alpha_1,\alpha_2,...,\alpha_s∈ V_\lambda \Rightarrow k_1\alpha_1+k_2\alpha_2 + ... + k_s\alpha_s∈V_\lambda,k_i∈ Cα1,α2,...,αs∈Vλ⇒k1α1+k2α2+...+ksαs∈Vλ,ki∈C
(5)V λ V_\lambdaVλ 是 n nn 维复向量空间的子空间
λ \lambdaλ 是 A AA 的特征值 ⇔ \Leftrightarrow⇔ V λ ≠ 0 V_\lambda ≠{0}Vλ=0
V λ V_\lambdaVλ 称为 A AA 的特征值 λ \lambdaλ 的特征子空间
如何理解“实对称矩阵只用对同一特征值对应的特征向量进行正交化”
引发这个思考的原因来自一类线性代数题:
已知矩阵 A = ? A=?A=?(实对称矩阵)
(1)求可逆矩阵 P PP,使得 P − 1 A P P^{-1}APP−1AP 为对角矩阵
(2)求正交矩阵 Q QQ,使得 Q T A Q Q^{T}AQQTAQ 为对角矩阵
复习全面的同学肯定很熟练地就能计算出来。
第一问:将每个特征值对应的全部线性无关的特征向量排在一起;
第二问:将同一个特征值对应的全部线性无关的特征向量进行施密特正交化后,对全部特征向量进行规范化,再将全部线性无关的特征向量排在一起.
\space
我们都知道实对称矩阵不同特征值对应的特征向量不仅线性无关,而且还正交(这个比较容易证明);所以我们只需要对同一特征值对应的全部特征向量进行正交化。
但是你可能从未见过一类题,“规定矩阵 A AA 不是实对称矩阵,要求求正交矩阵 Q QQ,使得 Q T A Q Q^{T}AQQTAQ 为对角矩阵”,因为非实对称矩阵相似对角化过程中不可对特征向量进行正交规范化。
\space
这是为什么呢?下面就将讲解原因。
“非实对称矩阵相似对角化过程中不可对特征向量进行正交规范化”的根本原因在于不同特征值对应的特征向量进行施密特正交化会导致新向量对应的特征值发生改变。
举个例子二维向量的例子,假设 A = ( 1 − 1 0 2 ) A=\left(\begin{matrix} 1 & -1 \\ 0 & 2 \end{matrix}\right)A=(10−12),其特征值 λ 1 = 1 、 λ 2 = 2 \lambda_1=1、\lambda_2 = 2λ1=1、λ2=2,对应的特征向量分别为 α 1 = ( 1 0 ) 、 α 2 = ( 1 − 1 ) \alpha_1=\left(\begin{matrix} 1 \\ 0 \end{matrix}\right)、\alpha_2=\left(\begin{matrix} 1 \\ -1 \end{matrix}\right)α1=(10)、α2=(1−1),将它们正交化得到 β 1 = ( 1 0 ) 、 β 2 = ( 0 1 ) \beta_1=\left(\begin{matrix} 1 \\ 0 \end{matrix}\right)、\beta_2=\left(\begin{matrix} 0 \\ 1 \end{matrix}\right)β1=(10)、β2=(01)。但很显然,A β 2 ≠ λ 2 β 2 A\beta_2≠\lambda_2\beta_2Aβ2=λ2β2,也就是说正交化后的 β 2 \beta_2β2 对应的特征值不再是 λ 2 \lambda_2λ2 了。
为什么“不同特征值对应的特征向量进行施密特正交化会导致新向量对应的特征值发生改变”
可视化上面的例子: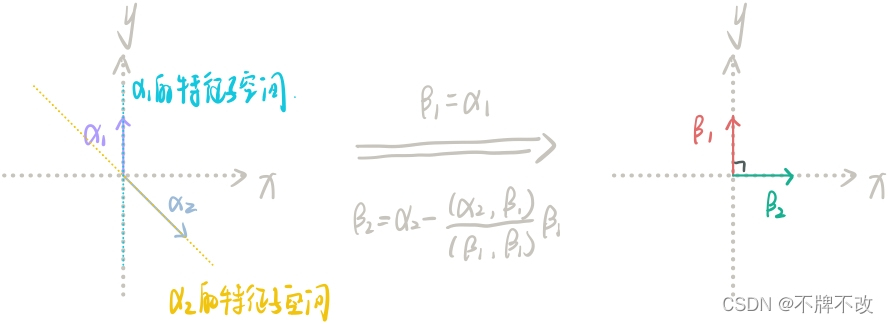
经过施密特正交化确实让两个向量正交了,但是根据特征值与特征向量的如下性质,由于 β 2 \beta_2β2 不能由 α 2 \alpha_2α2 线性表示,所以 β 2 \beta_2β2 不是特征值 λ 2 \lambda_2λ2 的特征向量,也即 β 2 \beta_2β2 不在 λ 2 \lambda_2λ2 的特征子空间中,所以 β 2 \beta_2β2 对应的特征值也就不是 λ 2 \lambda_2λ2。这样一来正交化就失去了意义。
性质:若 α 1 , α 2 , . . . , α t \alpha_1,\alpha_2,...,\alpha_tα1,α2,...,αt 都是矩阵 A AA 的属于特征值 λ \lambdaλ 的特征向量,则当 k 1 α + k 2 α 2 + . . . + k t α t k_1\alpha_+k_2\alpha_2+...+k_t\alpha_tk1α+k2α2+...+ktαt 非零时,k 1 α + k 2 α 2 + . . . + k t α t k_1\alpha_+k_2\alpha_2+...+k_t\alpha_tk1α+k2α2+...+ktαt 仍是矩阵 A AA 属于特征值 λ \lambdaλ 的特征向量。
为了更清楚地展示,我们扩展到三维空间中。
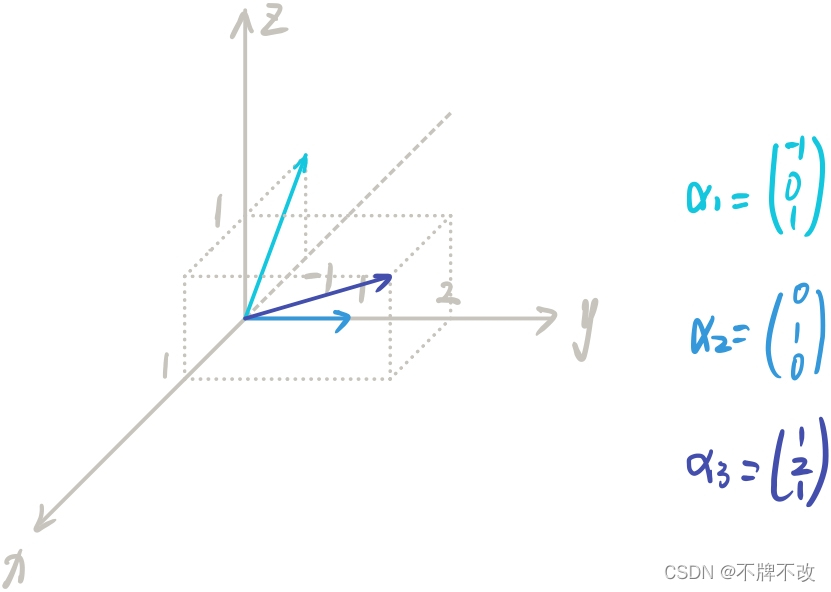
假设矩阵 A = ( 3 2 0 1 2 0 2 0 1 2 0 3 2 ) A=\left(\begin{matrix} \frac{3}{2} & 0 & \frac{1}{2} \\ 0 & 2 & 0 \\ \frac{1}{2} & 0 & \frac{3}{2} \end{matrix}\right)A=⎝⎛2302102021023⎠⎞ 为三阶实对称矩阵,其三个特征值分别为 λ 1 = 1 、 λ 2 = 2 、 λ 3 = 2 \lambda_1=1、\lambda_2=2、\lambda_3=2λ1=1、λ2=2、λ3=2,其中 λ 2 = λ 3 \lambda_2 = \lambda_3λ2=λ3,由于实对称矩阵线性无关的特征向量个数一定与阶数相同,所以 λ 1 \lambda_1λ1 对应的特征向量为 α 1 = ( − 1 , 0 , 1 ) T \alpha_1=(-1,0,1)^Tα1=(−1,0,1)T,λ 2 \lambda_2λ2 和 λ 3 \lambda_3λ3 对应的特征向量分别为 α 2 = ( 0 , 1 , 0 ) T \alpha_2=(0,1,0)^Tα2=(0,1,0)T 和 α 3 = ( 1 , 2 , 1 ) T \alpha_3=(1,2,1)^Tα3=(1,2,1)T,且不同特征值对应的特征向量正交,即 ( α 1 , α 2 ) = 0 (\alpha_1,\alpha_2)=0(α1,α2)=0,( α 1 , α 3 ) = 0 (\alpha_1,\alpha_3)=0(α1,α3)=0,α 2 \alpha_2α2 和 α 3 \alpha_3α3 不正交。
假设 α 1 \alpha_1α1、α 2 \alpha_2α2 和 α 3 \alpha_3α3 在三维空间中如下:
对 α 2 \alpha_2α2 和 α 3 \alpha_3α3 进行施密特正交化后:
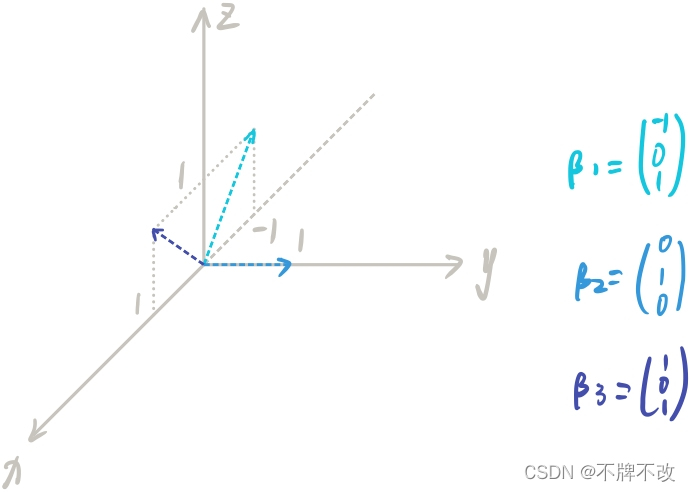
计算可以发现三个向量是两两正交的,且 β 2 \beta_2β2 和 β 3 \beta_3β3 对应的特征值还是 2 22。
如果我们处理的矩阵 A AA 不是一个实对称矩阵,只是一个一般矩阵,那么也就是说即使是不同的特征值对应的特征向量也不一定正交,如果我们对不同特征值对应的两个特征向量进行正交化会发生什么?
首先我们要明确一点,如果 λ \lambdaλ 的特征子空间是由两个线性无关的向量确定的,那么该特征值的特征子空间应该为由这两个线性无关的向量确定的平面内的全部向量组成,也就是说满足该特征值的特征向量应该在该平面内,不满足该特征值的向量都在平面外。
假设对于一个非实对称三阶矩阵 A AA 而言,其特征值记为 λ 1 、 λ 2 、 λ 3 \lambda_1、\lambda_2、\lambda_3λ1、λ2、λ3,其中 λ 2 = λ 3 \lambda_2 = \lambda_3λ2=λ3,假设三个特征值对应的特征向量 α 1 \alpha_1α1、α 2 \alpha_2α2 和 α 3 \alpha_3α3 如下:
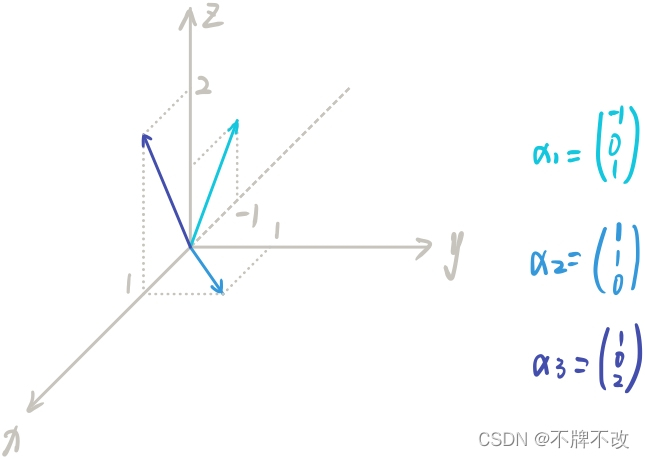
很显然三者都不是正交的。
如果对 α 2 \alpha_2α2 和 α 3 \alpha_3α3 进行施密特正交化,由于正交化只是对两个向量进行加法和数乘操作,所以不会影响二者构成的平面,也就是说 α 2 \alpha_2α2 和 α 3 \alpha_3α3 经过施密特正交化后得到的 β 2 \beta_2β2 和 β 3 \beta_3β3 仍是在 α 2 \alpha_2α2 和 α 3 \alpha_3α3 所构成的平面内,即 β 2 \beta_2β2 和 β 3 \beta_3β3 处于同一个特征值的特征子空间中,即施密特正交后二者的特征值没有发生改变。
如果对 α 1 \alpha_1α1 和 α 2 \alpha_2α2 进行施密特正交化,将 α 2 \alpha_2α2 视为 β 1 \beta_1β1,将 α 1 \alpha_1α1 转换为 β 2 \beta_2β2,则可以得到 β 1 = α 2 = ( 1 , 1 , 0 ) T \beta_1 = \alpha_2 = (1, 1, 0)^Tβ1=α2=(1,1,0)T,β 2 = ( 1 2 , 1 , 1 2 ) T \beta_2 = (\frac{1}{2}, 1, \frac{1}{2})^Tβ2=(21,1,21)T,作图如下:

其中淡蓝色虚线表示的是 λ 1 \lambda_1λ1 的特征子空间,即一维空间。经过施密特正交化后 λ 1 \lambda_1λ1 对应的特征向量 α 1 \alpha_1α1 变成了 ( 1 2 , 1 , 1 2 ) T (\frac{1}{2}, 1, \frac{1}{2})^T(21,1,21)T,很显然该向量已经不在 λ 1 \lambda_1λ1 的特征子空间中了,这说明 β 2 = ( 1 2 , 1 , 1 2 ) T \beta_2 = (\frac{1}{2}, 1, \frac{1}{2})^Tβ2=(21,1,21)T 对应的特征值不是 λ 1 \lambda_1λ1;
类似地,也可以将 α 1 \alpha_1α1 视为 β 1 \beta_1β1,将 α 2 \alpha_2α2 转换为 β 2 \beta_2β2,经过施密特正交化后会发现 β 2 \beta_2β2 已经不在由 α 2 \alpha_2α2 和 α 3 \alpha_3α3 构成的平面内,说明 β 2 \beta_2β2 的特征值发生改变。
通过上面的例子,可以总结出之所以不同特征值对应的特征向量进行施密特正交化会导致新向量对应的特征值发生改变,是因为施密特正交化的本质是向量的加法和数乘,对于同一个特征子空间内的向量进行施密特正交化后得到的向量仍在原特征子空间中,但不同特征子空间的向量进行正交化就不好说了。
汤家凤的教案上提到一个性质:
设 A AA 为 n nn 阶矩阵,λ 1 \lambda_1λ1,λ 2 \lambda_2λ2 为 A AA 的两个不相同的特征值,又 A α = λ 1 α A\alpha=\lambda_1\alphaAα=λ1α,A β = λ 2 β A\beta=\lambda_2\betaAβ=λ2β(α \alphaα 和 β \betaβ 为非零向量),对任意的 a ≠ 0 a≠0a=0,b ≠ 0 b ≠ 0b=0,向量 a α + b β a\alpha+b\betaaα+bβ 一定不是特征向量。
\space
施密特正交化就是一个线性组合的过程,根据该性质也可以说明不同特征值对应的特征向量进行正交化得到的不是特征向量。
做题时的施密特正交化
如果要计算一个正交矩阵 Q QQ,使得 Q T A Q = Λ Q^TAQ=\LambdaQTAQ=Λ,则 A AA 一定是一个实对称矩阵,且需要对同一个特征值对应的特征向量进行施密特正交,再对全部的特征向量进行规范化,将规范化后的特征向量排列起来得到 Q QQ;
如果要计算一个可逆矩阵 P PP,使得 P − 1 A P = Λ P^{-1}AP=\LambdaP−1AP=Λ,则 A AA 的要求就没那么苛刻了。如果 A AA 是非实对称矩阵,那么 P PP 一定不能化成正交矩阵。