LeetCode887：鸡蛋掉落

如题：

题目要求：探测出鸡蛋在一栋n层高的楼中最高在第x层扔下不摔碎，最少需要探测几次，给k颗鸡蛋探测

众所周知：一个鸡蛋要探测n层楼必须从第一层开始往上线性探测，最差的情况就要探测n次（第n层才碎），因为只有一颗

使用动态规划的方法完成该题，首先需要确定dp函数/数组的定义以及状态转移方程

思路一

• 如果dp函数的定义是dp(k,N)表示k个鸡蛋从N层楼探测返回的最小探测次数，那么就必须每层楼遍历，找最小的探测次数那一层楼返回的次数

  • 从1楼扔到N楼，每楼都扔，找出N个结果中最小的

    • 而每楼扔完之后分为碎了和没碎两种情况：碎了就去1到当前层-1层再扔，同时鸡蛋-1；没碎就去当前层+1到N层之间扔，鸡蛋数不变
    • 碎的情况下扔的次数和没碎的情况下扔的次数不一样时，我们要取更大的最差结果，因为要保证真的发生最差情况的时候能探测完
    • 每层楼都要试，然后取所有楼层中最小的

    //K表示剩余鸡蛋多少，N表示总共有N层楼
    int dp(int K, int N):
        for 1 <= i <= N:
            // 最坏情况下的最少扔鸡蛋次数
            res = min(res, 
                      max( 
                        dp(K - 1, i - 1), // 碎
                        dp(K, N - i)      // 没碎，去i+1到N楼搜，总共是N-i楼
                      ) + 1 // 在第 i 楼扔了一次
                     )
        return res
    

  • 搜索楼层的时候由于有鸡蛋限制，不能直接用二分搜索探测，否则鸡蛋只剩1个的时候只能从1层开始层层探测到当前层

  • 但如果没有鸡蛋限制，直接二分搜索是最快的，即探测mid，碎了去lo-mid-1探测，没碎去mid+1-high探测

  • 如果加上鸡蛋限制，不能根据鸡蛋碎了还是没碎决定去哪一半区间探测，要根据鸡蛋碎的时候的探测次数和鸡蛋没碎的时候的探测次数比较

    • 看原来的代码

      // 最坏情况下的最少扔鸡蛋次数
      res = min(res, 
                max( 
                    dp(K - 1, i - 1), // 碎
                    dp(K, N - i)      // 没碎，去i+1到N楼搜，总共是N-i楼
                ) + 1 // 在第 i 楼扔了一次
               )
      

      • 找每一层最坏情况中最少的扔鸡蛋次数，思考该层什么情况下是所有楼层中扔鸡蛋次数最少的那一层？

      • 由于碎了和没碎的时候探测次数和楼层高度是成正比的，即探测的楼层更多，探测次数肯定更多

        • 碎了的时候dp(K-1,i-1)随着楼层i增加要搜索的层数变多

        • 没碎的时候dp(K,N-i)随着楼层i增加要搜索的层数变少

        • 那么就是说这两种情况一个递增一个递减，每次我们在当前层探测的次数取两种情况更大的，那么一单调增一单调减的时候取两者最大，返回的结果最少的情况就是两者相等的时候：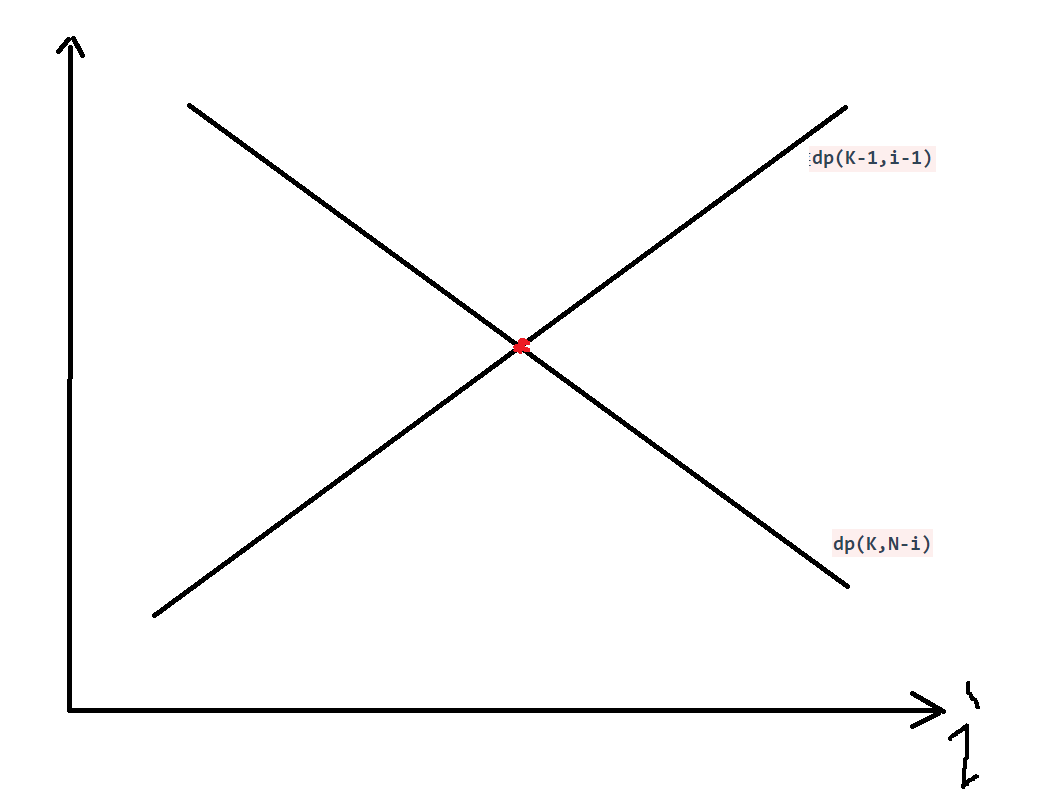

          
          • 可以看到两个函数取最大值的话，红点处就是最小的结果
          • 那么在探测楼层的时候就可以不用每层楼都探测然后找所有楼层中最小的
            • 我们直接取中间楼层扔鸡蛋，不同的是不是根据鸡蛋碎没碎而决定排除哪一半区域，而是根据根据当前楼层中dp(K-1,i-1)和dp(K,N-i)谁更大来决定排除一半区域，这是根据状态转移方程本身的单调性才有的二分，而不是思路上采用了二分搜索，我们思路仍然是要遍历所有楼层找最小的一层，只不过状态转移方程具有单调性。

• 代码：

class Solution {
    //备忘录，memo[K][N]直接记录K颗鸡蛋探测N楼最少要探测多少次
    int[][] memo;

    public int superEggDrop(int K, int N) {
        //楼层从1开始，鸡蛋个数也从1开始，需要+1
        memo = new int[K + 1][N + 1];
        for (int[] m : memo) {
            //随便初始化备忘录，记录的探测次数是>0的，因此直接随便填一个负数
            Arrays.fill(m, -888);
        }
        return dp(K, N);
    }

    private int dp(int K, int N) {
        if (K == 1) return N;
        if (N == 0) return 0;
        //如果不是初始化的值，就意味着当前状态的值已经记录下来了，直接返回
        if (memo[K][N] != -888) return memo[K][N];
        int res = Integer.MAX_VALUE;
        //原来是这样，现在进行优化
//        for (int i = 1; i <= N; i++) {
//            res = Math.min(res, Math.max(dp(K - 1, i - 1), dp(K, N - i)) + 1);
//        }
        int lo = 1;
        int hi = N;
        while (lo <= hi) {
            int mid = lo + (hi - lo) / 2;
            int down = dp(K - 1, mid - 1);//鸡蛋碎了，往下探测要探测多少次
            int up = dp(K, N - mid);//鸡蛋没碎，往上探测要探测多少次
            if (down < up) {//如果往上探测要的次数更多，就表示此时在交点左侧，需要将左边界右移
                lo = mid + 1;
                res = Math.min(res, up + 1);
            } else if (down > up) {//如果往下探测次数更多，就表示此时在交点右侧，需要将右边界左移
                hi = mid - 1;
                res = Math.min(res, down + 1);
            } else {//如果上下探测次数一样，表示此时就是探测次数最少的那一层，记录当前探测次数，退出循环
                res = up + 1;
                break;
            }
        }
        memo[K][N] = res;
        return res;
    }

}

思路二

• 反向思考， 考虑k颗鸡蛋探测m次能在一栋h高的楼中找出最高不会摔碎的楼层，操作m来让h逼近n

  • 例如(4,6)=h表示我们用4颗鸡蛋探测6次能在h高的楼中探测出鸡蛋最高不会摔碎的楼层
    • base case:直到鸡蛋只剩一颗，此时能探测的层数等于探测次数；或者探测次数只剩一次，此时只能探测一层
    • 我们需要一个dp[][]数组，dp[4][6]=h，从数组的第二行第二列开始从左往右计算每一行，因为第一行表示鸡蛋只有一颗，是base case，第一列表示探测次数只有一次，也是base case
    • 如果碎了鸡蛋-1，探测次数-1，也就是求(3,5)能探测h1层
    • 如果没碎鸡蛋不变，探测次数-1，也就是求(4,5)能探测h2层
    • 最终能探测h1+h2+1=h层
    • 也可以算出第一次探测的位置应该是(3,5)+1的位置
  • 可以想象成给一栋楼划分层数，（2,7）表示两个鸡蛋探测七次可以给一栋楼划分成几层，从第x层开始探测
    • 碎了时候是（1,6），此时是base case，直接返回能划分成6层，因为必须一层一层划分
    • 没碎的时候是（2,6），继续上一步，直到碰到base case，最终得到21
    • 最后的结果就是21+6+1=28层，也就是说2颗鸡蛋要在28层的楼中确定限界摔碎楼层要探测7次。如果28>题目给的层数就返回7
    • （1,6）+1的位置就是第一次探测开始的位置，此时(1,6)+1=6+1=7，表示第一次从第7层开始探测，因此可以看出不能单纯用二分探测，否则第一次就从14开始了

• 代码

  class Solution {
      public int superEggDrop(int K, int N) {
          // m 最多是N次，比如从第一层开始层层往上
          int[][] dp = new int[K + 1][N + 1];
          int m = 0;
          while (dp[K][m] < N) {
              m++;
              //这里包含了base case，鸡蛋数k是行，探测次数m是列，只能探测一次的时候表示第一列，此时能探测的层数都是1层
              //只有一颗鸡蛋的时候是第一行，此时探测层数=探测次数，dp[1][1]=1，dp数组从第一行第一列开始往右边递增
              for (int k = 1; k <= K; k++)
                  dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1;
          }
          System.out.println(dp[K][m]);
          return m;
      }
  }