Python 实现逻辑斯蒂回归模型

class LogisticRegression:
    def __init__(self, penalty='l2', gamma=0, fit_intercept=True):
        self.penalty = penalty
        self.gamma = gamma
        self.fit_intercept = fit_intercept
        self.weights = None
        self.parameters = {}
        
    def __repr__(self):
    	if self.parameters:
            return 'LogisticRegression(lr={lr},tol={tol},max_iter={max_iter})'.format_map(self.parameters)
        else:
            return '{}()'.format(self.__class__.__name__)
        
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))
        
    def fit(self, X, y, lr=0.1, tol=1e-7, max_iter=1e7):
        self.parameters['lr'] = lr
        self.parameters['tol'] = tol
        self.parameters['max_iter'] = max_iter 
        if self.fit_intercept:
            X = np.c_[np.ones(X.shape[0]), X]
        cur_loss = np.inf
        self.weights = np.random.rand(X.shape[1])
        for _ in range(int(max_iter)):
            y_pred = self.sigmoid(np.dot(X, self.weights))
            loss = self._NLL(X, y, y_pred)
            if loss - cur_loss < tol:
                break
            cur_loss = loss
            self.weights -= lr * self._NLL_grad(X, y, y_pred)
        return self
            
    def _NLL(self, X, y, y_pred):
        
        weights, gamma = self.weights, self.gamma 
        
        order = 2 if self.penalty == "l2" else 1
        norm_w = np.linalg.norm(self.weights, ord=order)
        nll = -np.log(y_pred[y==1]).sum() - np.log(1-y_pred[y==0]).sum()
        penalty = (gamma / 2) * norm_w ** 2 if self.penalty == 'l2' else gamma * norm_w
        
        return (nll + penalty) / X.shape[0]
        
    def _NLL_grad(self, X, y, y_pred):
    
        weights, gamma = self.weights, self.gamma 
        penalty_grad = gamma * weights if self.penalty == 'l2' else gamma * np.sign(weights)
        return -(np.dot(y - y_pred, X) + penalty_grad) / X.shape[0]
    
    
    def predict(self, X):
        if self.fit_intercept:
            X = np.c_[np.ones(X.shape[0]), X]
        return self.sigmoid(np.dot(X, self.weights))

构造数据集

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0,1,-1]])
    # print(data)
    return data[:,:2], data[:,-1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

lr = LogisticRegression()
lr.fit(X_train,y_train,max_iter=20000)

LogisticRegression(lr=0.1,tol=1e-07,max_iter=20000)

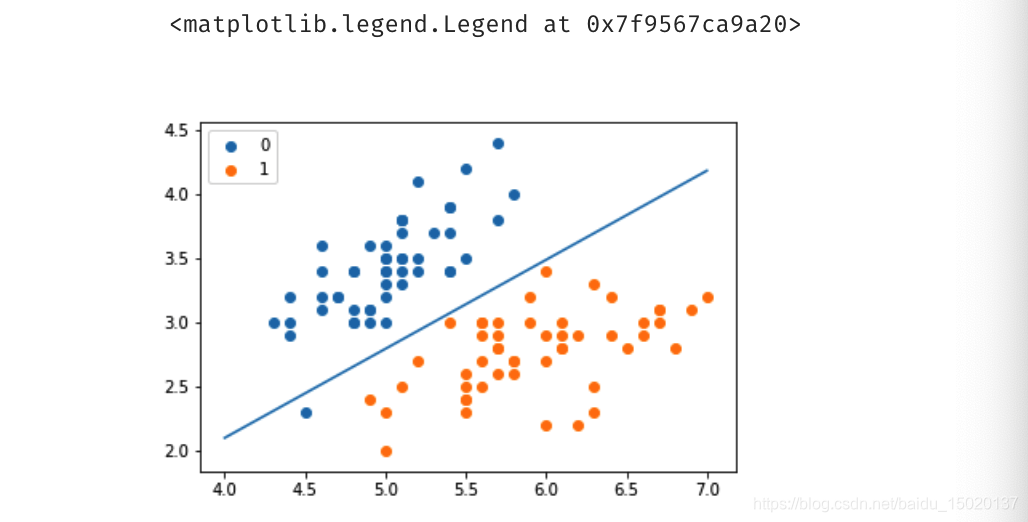
画图验证一下效果

x_ponits = np.arange(4, 8)
y_ = -(lr.weights[1]*x_ponits + lr.weights[0])/lr.weights[2]
plt.plot(x_ponits, y_)

plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()