Matplotlib是一个主要用于绘制二维图形的Python库。数据可视化是数据分析的重要环节，借助图形能够更加直观地表达出数据背后的“东西”。Matplolib最初主要模仿Matlab的画图命令，但是它是独立于Matlab的，可以自由、免费使用的绘图包。Matplotlib依赖NumPy库可以提供出色的绘图能力。
Matplotlib的官网地址为：http://matplotlib.org/。
MatplotlibAPI的详细介绍请参考官网地址：
http://matplotlib.org/api/index.html。
1
散点图
散点图显示两组数据的值，如图1-1所示。每个点的坐标位置由变量的值决定，并由一组不连接的点完成，用于观察两种变量的相关性。例如，身高—体重、温度—维度。
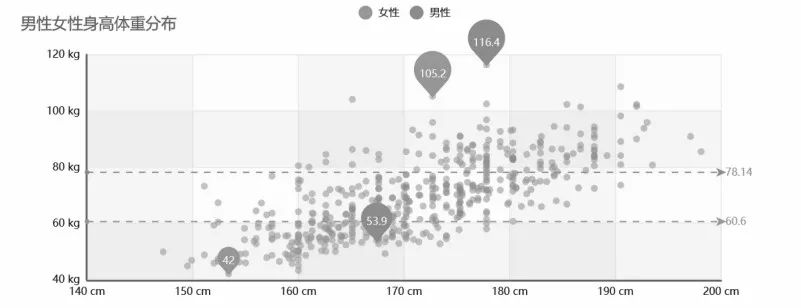
图1-1 散点图示例
使用Matplotlib的scatter()函数绘制散点图，其中x和y是相同长度的数组序列。scatter()函数的一般用法为：
主要参数说明如下：
• x,y：数组。
• s：散点图中点的大小，可选。
• c：散点图中点的颜色，可选。
• marker：散点图的形状，可选。
• alpha：表示透明度，在 0~1 取值，可选。
• linewidths：表示线条粗细，可选。
示例：绘制身高—体重的散点图
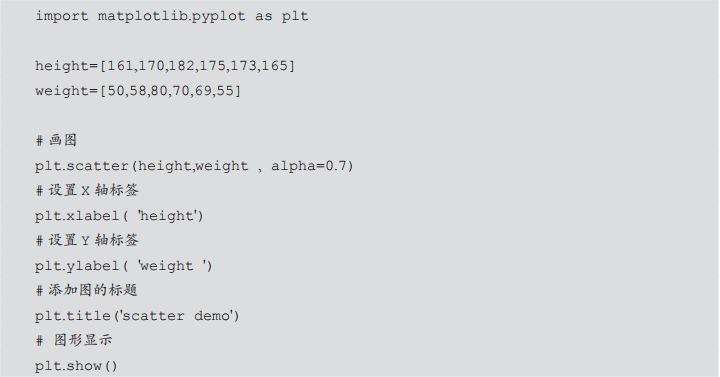
运行脚本输出如图1-2所示的图形。
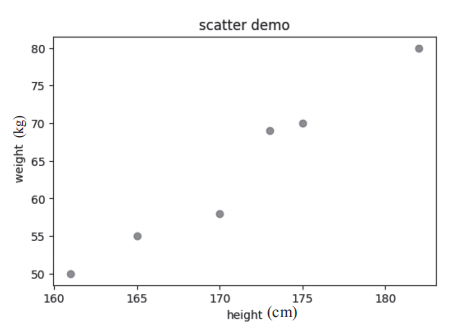
图1-2 基本的散点图
散点图主要演示两个变量的相关性：正相关、负相关、不相关。
2
折线图
折线图也称条形图，是用直线将各个数据连接起来组成的图形，如图2-1所示。常用来观察数据随时间变化的趋势。例如，股票价格、温度变化等。
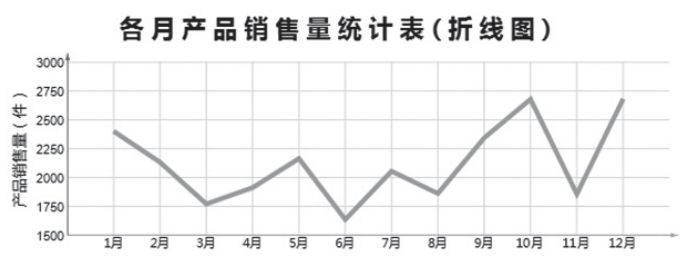
图2-1 折线图
图2-1所示的折线图是某公司近5年的汽车销售数据，折线图的横坐标是时间，纵坐标是销售量，表示随着时间的推移，销售量的变化趋势。
使用Matplotlib的plot()函数绘制折线图，其中x和y是相同长度数组序列。plot ()函数的使用方法可以参考其官网介绍。
地址为：
http://matplotlib.org/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot。
示例：显示y=2x+1的图形
Matplotlib中最基础的模块是Pyplot, 下面从最简单的线图开始讲解。例如，有一组数据，还有一个拟合模型，通过编写代码来实现数据与模型结果的可视化。
假设一个线性函数具有形式y=ax+b, 自变量是x，因变量是y，y轴截距为b，斜率为a。
下面用简单的数据来描述线性方程y=2x+1，代码如下：
运行脚本输出如图2-2所示的图形。
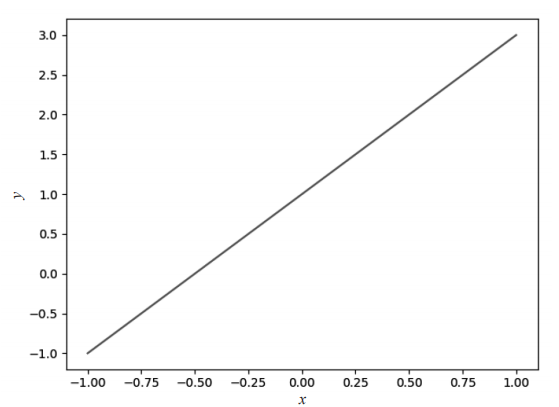
图2-2 基本直线图
在图2-2中，使用线性方程y=2x+1画出的是直线图。如果想画出曲线图，则只需更改线性方程为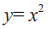
，完整代码如下：
运行脚本输出如图2-3所示的图形。
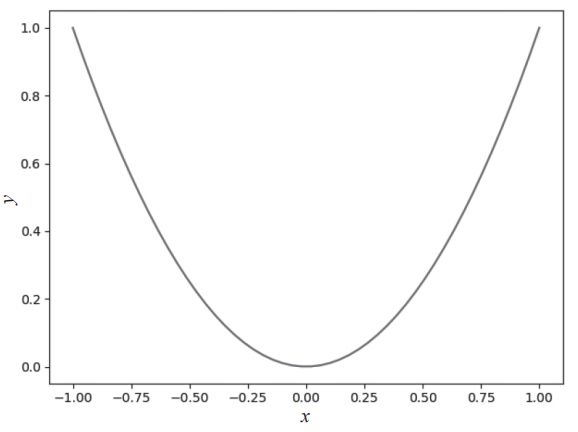
图2-3 曲线图
3
柱状图
柱状图也称条形图，以长方形的长度为变量的统计视图，如图3-1所示。用来比较多个类别的数据大小，通常用来比较两个或以上的变量。如果只有一个变量，通常用于较小的数据集分析。
例如，不同季度的销量、不同国家的人口等。
图3-1 条形图
使用Matplotlib的bar()函数绘制柱状图，其中x和y是相同长度数组序列。bar()函数的一般用法为：
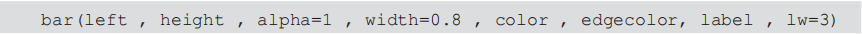
参数说明如下：
• left：x轴的位置序列，是横坐标。一般采用NumPy的arange函数产生一个序列。
• height：y轴的数值序列，也就是柱形图的高度。一般是需要展示的数据。
• alpha：透明度。
• width：柱形图的宽度。
• color：柱形图填充的颜色。
• edgecolor：图形边缘颜色。
• label：解释每个图形代表的含义。
• lw：线的宽度。
示例：垂直柱状图
本例文件名为
“PythonFullStack\Chapter07\mpl_bar01”
显示垂直柱状图。其完整代码如下：
运行脚本输出如图3-2所示的图形。
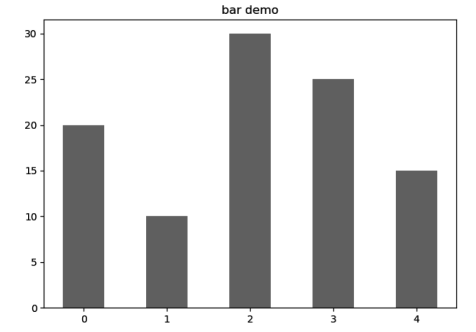
图3-2 垂直柱状图
4
直方图
直方图由一系列高度不等的纵向条形组成，表示数据分布的情况。例如，某年级学生的身高分布情况，如图4-1所示。
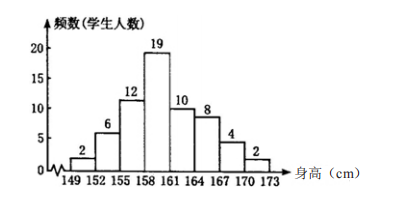
图4-1 直方图
直方图与柱状图的区别有以下几点：
(1)柱状图是用条形的长度表示各类别频数的多少，其宽度(表示类别)是固定的，主要是展示不同类别的数据。
(2)直方图是用面积表示各组频数的多少，矩形的高度表示每一组的频数 ( 或频率 )，宽度则表示各组的组距，因此其高度与宽度均有意义。
(3)由于分组数据具有连续性，因此直方图的各矩形通常是连续排列，而柱状图则是分开排列。
(4)柱状图主要用于展示分类型数据，而直方图主要用于展示数据型数据。
使用Matplotlib的hist()函数绘制直方图，hist()函数的一般用法为：
主要参数说明如下：
• bins：直方图中箱子 (bin) 的总个数。个数越多，条形带越紧密。
• color：箱子的颜色。
• normed：对数据进行正则化。决定直方图y轴的取值是某个箱子中的元素的个数 (normed=False), 还是某个箱子中的元素的个数占总体的百分比 (normed=True)。
在介绍直方图之前，先来了解什么是正太分布。
正态分布也称常态分布，是连续随机变量概率分布的一种，自然界、人类社会、心理和教育中的大量现象均按正态形式分布。例如，能力的高低、学生成绩的好坏等都属于正态分布。正态分布曲线呈钟形，两头低，中间高，左右对称。因其曲线呈钟形，所以人们又经常称之为钟形曲线，如图4-2所示。
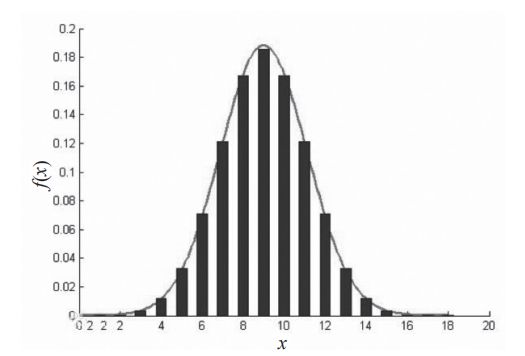
图4-2 正态分布的钟形曲线
正态分布有两个参数，即均值和标准差。均值是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为：取与均值越近的值的概率越大，而取离均值越远的值的概率越小。
标准差描述正态分布资料数据分布的离散程度，标准差越大，数据分布越分散；标准差越小，数据分布越集中。标准差也是正态分布的形状参数，标准差越大，曲线越扁平；反之，标准差越小，曲线越瘦高。
绘制直方图，需要使用NumPy的np.random.randn(N)函数，这个函数的作用就是从标准正态分布中返回N个样本值。
示例：直方图
本例文件名为
“PythonFullStack\Chapter07\mpl_hist01”
显示直方图。其完整代码如下：
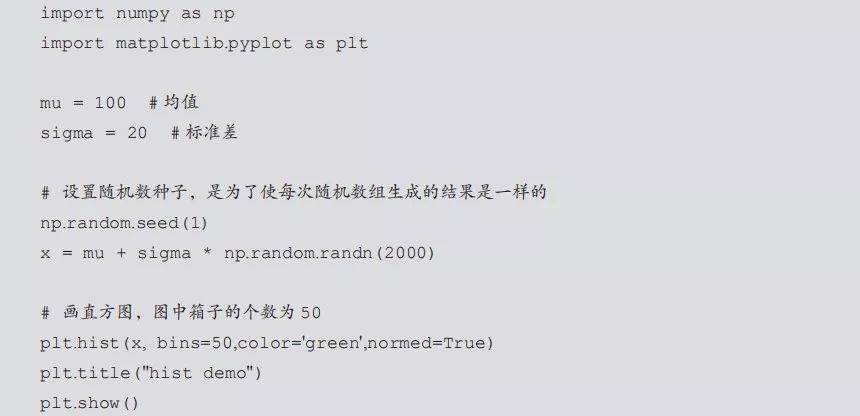
运行脚本输出如图4-3所示的图形。
图4-3 直方图
5
饼状图
饼状图显示一个数据系列中各项的大小与各项总和的比例。饼状图中的数据点显示为整个饼状图的百分比。例如，2018年第一季度虚拟的全国手机各品牌出货量市场份额图，如图5-1所示。
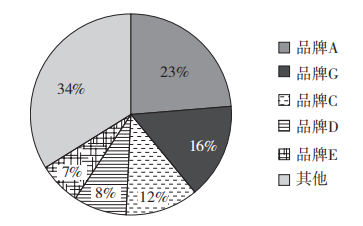
图5-1 手机品牌占市场份额图
使用Matplotlib的pie() 函数绘制饼状图，pie() 函数的一般用法为：
主要参数说明如下：
• x：每一块饼状图的数据。
• labels：每一块饼状图外侧显示的说明文字。
• autopct：控制饼状图内百分比设置，可以使用format字符串或者format function，如 “%1.1f”指小数点前1位数，小数点后1位数。
• shadow：是否阴影，可选值True和False。
• explode：每一块饼状图离开中心的距离。
示例 ：饼状图
本例文件名为
“PythonFullStack\Chapter07\mpl_pie01”
显示饼状图。其完整代码如下：
运行脚本输出如图5-2所示的图形。
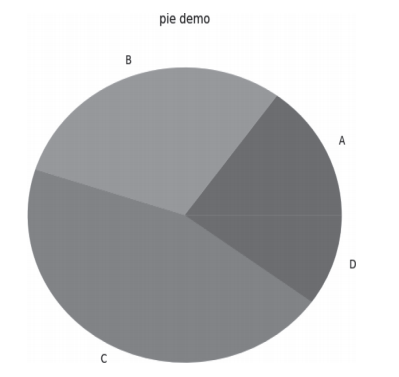
图5-2 不规则饼状图
从图5-2中可以发现，这个饼状图不是正圆的，因为在绘图的时候，它的x轴和y轴的比例不是1：1。为了节省篇幅，把上例代码plt.axes(aspect=1)前的注释符 "#" 省略，并保证它在plt.pie()函数前，再运行脚本就得到完美的正圆饼状图了，如图5-3所示。
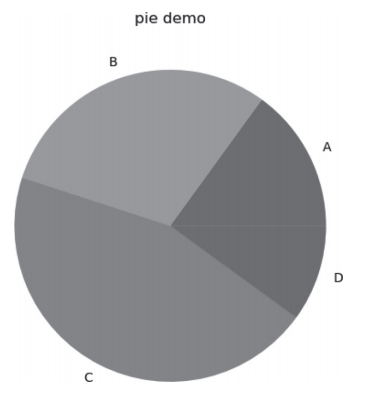
图5-3 正圆的饼状图
---------------------------------------------------------------------
文中观点来源于
北京大学出版社
《Python 3.x全栈开发从入门到精通》
▼
全新：本书理论、技术与案例基于全新的Python 3.x。
全面：涵盖Python全栈开发全过程，知识点涉及数据分析、数据存储、数据可视化、系统网络运维、Web项目和量化交易等多领域。
实战：海量示例文件展示开发过程中的重点、疑点、难点。基础：零基础也能入门，拆解式讲解全栈开发过程中的知识和技术。
丰富：本书配套的源代码全部赠送，资源丰富，可轻松复制所需项目内容。
购买地址：
点击左下文末“
好书备齐，多元学力，品质图书每满100减50
✍
我写完了，有启发的话，记得点一下「在看」