python | 编译原理，语法分析——LL(1)文法实现 中

上一个文章实现了对LL(1)文法各非终结符求first集和follow集，我们这篇文章则是继续求得LL(1)的预测分析集。

看一下预测分析集的求解方法：

这里我们需要求对于一个串的first集，求解方法如下：

任意符号α的FIRST集求法：
1. α为终结符，则把它自身加入FIRSRT(α)
2. α为非终结符，则：
（1）若存在产生式α->a...，则把a加入FIRST(α),其中a可以为ε
（2）若存在一串非终结符Y1,Y2, ..., Yk-1，且它们的FIRST集都含空串，且有产生式α->Y1Y2...Yk...，那么把FIRST(Yk)-{ε}加入FIRST(α)。如果k-1抵达产生式末尾，那么把ε加入FIRST(α)
　　 注意（2）要连续进行，通俗地描述就是：沿途的Yi都能推出空串，则把这一路遇到的Yi的FIRST集都加进来，直到遇到第一个不能推出空串的Yk为止。
重复1,2步骤直至每个FIRST集都不再增大为止。

这地方借鉴自：【编译原理】语法分析LL(1)分析法的FIRST和FOLLOW集

通过这一步骤编写求一个串的first集合：

dirFirst = defaultdict(set)
def getDirFirst(curPro):
   res = []
   # 对于一个字符串求first集
   for i in range(1,len(curPro)):
       if curPro[i] in vt:
           res.append(curPro[i])
           break
       elif curPro[i] in vn:
           if 'epsilon' in first[curPro[i]]:
               res.extend(first[curPro[i]])
           else:
               res.extend(first[curPro[i]])
               break
   # 去重
   ress = []
   for i in res:
       if i not in ress:
           ress.append(i)
   return ress

对于文法G的每个产生式 A->α ，进行如下处理
（1）对于FIRST(α)中每个终结符号a，将 A->α 加入到 M[A,a] 中。
（2）如果 ε在FIRST(α)中，那么对于FOLLOW(A)中每个终结符号b，将 A->α 加入到 M[A,b] 中。如果 ε在FIRST(α)，且$在FOLLOW(A)中，也将A->\alpha 加入到M[A,$] 中。

求预测分析表：
1.先构建一个这样的表

2.然后依次填入非终结符号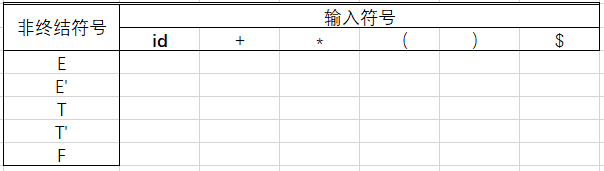

3.按照规则1填写其余内容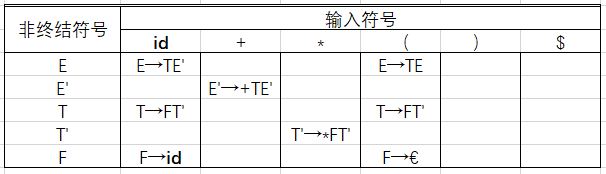

4.按照规则2填写内容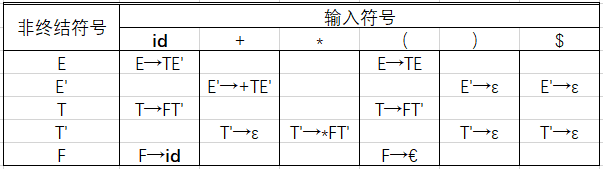

至此整个构建全部完成

此处借鉴自：FIRST集合、FOLLOW集合以及LL(1)文法

预测分析表中我们为了两个字符串作为两维表的索引，利用pandas中的DataFrame存储表格信息。

dfData = [[[] for i in range(len(vt))] for i in range(len(vn))]
M = pd.DataFrame(data = dfData,index=vn,columns=vt)
# print(M)
# print(M.loc['E']['+'])
def getM():
    #step1
    for curPro in productions:
        A = curPro[0]
        dirFirst = getDirFirst(curPro)
        # print(A)
        # print(dirFirst)
        for a in dirFirst:
            if a=='epsilon':
                continue
            M.loc[A][a].append(curPro)
    #step2
    for curPro in productions:
        A = curPro[0]
        dirFirst = getDirFirst(curPro)
        # print(curPro)
        # print(' ',dirFirst)
        if 'epsilon' in dirFirst:
            for b in follow[A]:
                M.loc[A][b].append(curPro)
getM()
print(M)

运行结果为：

id               (                )                 +  \                   * epsilon                $  
E   [[E, T, E']]    [[E, T, E']]               []                []                   []      []               []  
T   [[T, F, T']]    [[T, F, T']]               []                []                    []      []               []  
E'            []              []  [[E', epsilon]]  [[E', +, T, E']]                   []      []  [[E', epsilon]]  
T'            []              []  [[T', epsilon]]   [[T', epsilon]]   T [[T', *, F, T']]      []  [[T', epsilon]]  
F      [[F, id]]  [[F, (, E, )]]               []                []                    []      []               []