MATLAB的非线性方程

1、 主要有两个 solve 和 fsolve，一个是符号的，一个是数值的

2、非线性方程还要看是否是多项式和非多项式。
（1）多项式的方程，似乎可以用解析法求解，得到多个方程解。可以用数值的roots和符号的root，solve；但是如果用数值的fsolve和fzero进行求解，因为有初始点的要求，只能得到初始点附近的一个解。

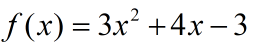
看代码：

数值类

roots解决

p = [3 4 -3];
r = roots(p)
r =
   -1.8685
    0.5352

fzero和fsolve解决

fun = @(x)3*x^2+4*x-3;
x0 = 3;
x1 = fzero(fun,x0)
x2 = fsolve(fun,x0)

x1 =
    0.5352
x2 =
    0.5352

分析：数值方面，只有root才能得到两个解，其他的根据初始解的位置得到附近的解。

符号类

solve和vpasolve

syms x
eqn = 3*x^2 + 4*x -3 == 0
solx = solve(eqn)
solnx = vpasolve(eqn)

solx =
 - 13^(1/2)/3 - 2/3
   13^(1/2)/3 - 2/3
solnx =
 -1.8685170918213297643730737558235
 0.53518375848799643103974042249017

syms x
p =3*x^2 + 4*x -3;
root(p,x)
ans =
 root(x^2 + (4*x)/3 - 1, x, 1)
 root(x^2 + (4*x)/3 - 1, x, 2)

分析：所有的符号函数求解都可以得到多个解。

（2）非多项式方程。

这种方程可能有很多个解的，比如sin(x)，这种的怎么办？就那这个当例子说明一下：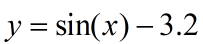

用solve和vpasolve求解，发现，一个是2个解，一个是1个解；
不能用root和roots求解；
用fsolve和fzeros求解，根据初始值，得到一个解；

3、待续。。。。