ARIMA模型即差分自回归移动平均模型,它是在AR、MA、ARMA模型的基础上,基于数据的平稳性构建的差分时间序列,ARIMA模型包含AR、MA、ARMA模型,所以学会操作ARIMA模型,也就相当于学会了AR、MA、ARMA模型。ARIMA(p,d,q)中,AR是"自回归",p为自回归项数;I为差分,d为使之成为平稳序列所做的差分次数(阶数);MA为"滑动平均",q为滑动平均项数。
1
数据及平稳性检验
对2019年6月19日-2020年6月19日格力电器股票的开盘价序列进行分析,数据如下:
然后进行平稳性检验,具体操作过程参见本公众号文章
《
Eviews中时间序列的平稳性、协整检验操作(一):ADF单位根检验》
ADF检验结果如下:

如图所示,NullHypothesis表示原假设是:rgdp序列具有一个单位根,即rgdp原序列为一个非平稳序列。ADF检验值为0.401554,对应p值=0.9985,大于0.05,在5%的显著性水平下接受原假设,rgdp序列具有单位根,是非平稳序列。
接下来检验一阶差分的GDP:

可以看到一阶差分后的rgdp仍然是非平稳的(p值大于0.05);
做二阶差分的rgdp:
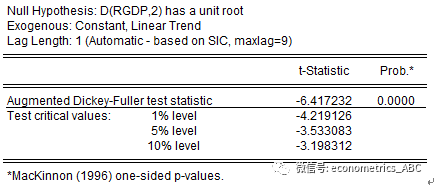
如图所示,NullHypothesis表示原假设是:二阶差分的rgdp序列具有一个单位根, ADF检验值为-6.417232,对应p值=0.0000,小于0.05,在5%的显著性水平下拒绝原假设,二阶差分rgdp序列不具有单位根,是平稳序列。
2
p,d,q的确定
经过以上验证,可以认为二阶差分rgdp序列是单整的平稳数据,即只需要建立ARMA(p,2,q)模型。ARMA(p,2,q)可以转化为AR()和MA(),其对应的特征为两种函数均表现为逐渐衰减的态势,在样本对应的ACF和PACF图形上,可以进行相应的判断。
首先生成二阶差分rgdp序列,在Eviews输入以下命令:
genr drgdp=rgdp-rgdp(-1)genr ddrgdp= drgdp-drgdp(-1)
然后进行自相关与偏自相关分析:
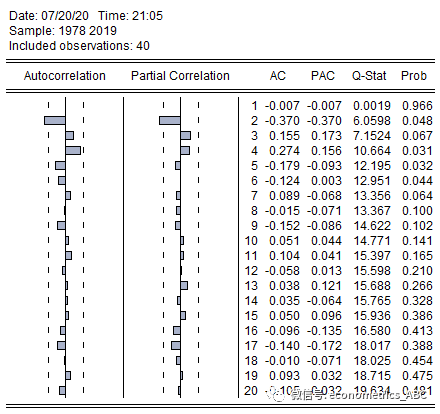
如图所示,ddrgdp的序列对应的ACF图形形在第2期就衰减为0,PACF图形也在第2期衰减为0,因此可以建立ddrgdp的ARMA(2,2),也就是ARIMA(2,2,2)模型。
3
估计模型
估计模型的未知参数,在Eviews输入以下命令:
ls ddrgdp c ar(1) ar(2) ma(1) ma(2)
得到结果:
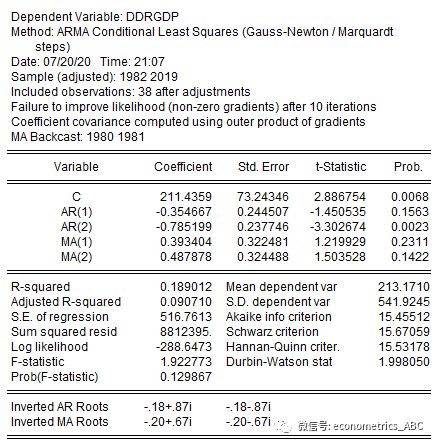
可以看到,AR(1)的估计系数为-0.354667,AR(2)的估计系数为-0.785199,MA(1)的估计系数为0.393404;MA(2)的估计系数为0.487878。
估计结果如下:
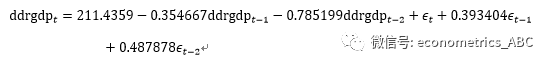
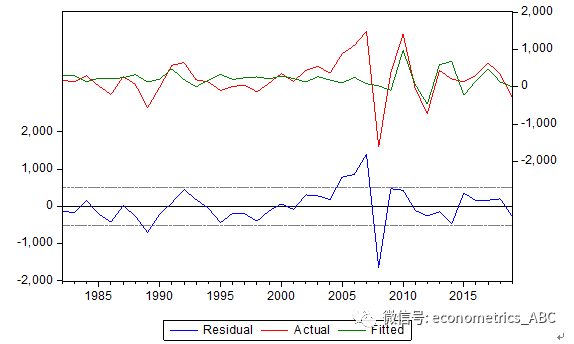
从ddrgdp残差图中观察可知,残差序列基本不具有序列相关性,除了2008年左右,残差的波动幅度基本在二倍置信区间之间,振幅小于5%。
4
预测
为了考察ARIMA(2,2,2)模型对ddrgdp的预测效果,根据此模型对2020年进行预测。
在Eviews中预测得到2020年的ddrgdp=195.0616,那么2020年的drgdp=195.0616+drgdp(2019)=195.0616+8321.219=8516.281,
那么,2020年的
rgdp=8516.281+rgdp(2019)=8516.281+144543.4804=153059.7614
欢迎扫码关注,若有问题,请点击“在看”留言或在公众号里留言。