matlab中使用一维向量来表示多项式,将多项式的系数按照降幂次序存放在行向量中,多项式中缺少的幂次的系数为0。
创建函数文件,将向量表示的多项式用字符串输出的函数:
%polynomial printf
function s=pprintf(p)
if nargin>1
error('too much input arguements')
end
%确认输入变量
while p(1)==0
p(1)=[];
end
%将高次的零去掉
l=length(p)%计算p的长度
if l==0
s='0';
elseif l==1
s=num2str(p(1));
elseif l==2
s=strcat(num2str(p(1)),'x+',num2str(p(2)));
elseif l>2
for i=1:l
if i==1
if p(i)==1
s=strcat('x^{',num2str(l-i),'}');
else
s=strcat(num2str(p(i)),'x^{',num2str(l-i),'}');
end
elseif i==l
s=strcat(s,'+',num2str(p(i))')
elseif i==l-1
s=strcat(s,'+',num2str(p(i)),'x');
else
if p(i)==0
else
s=strcat(s,'+',num2str(p(i)),'x^{',num2str(l-i),'}');
end
end
end
end
在命令行输入多项式处理命令:
p=[1 2 3];
s=@pprintf;
s(p)%pprintf(p);
输出结果如下: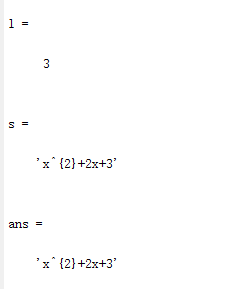
r=roots(p)%求解多项式的根(列向量)
输出结果如下:
p=poly(r)%给出多项式的跟,构造出相应的多项式
输出结果如下: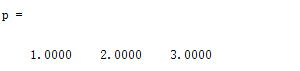
多项式的四则运算
(1)加
a=[1 3 5 7 9];
b=[1 2 4 6 8];
c=a+b
输出结果如下: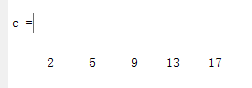
(2)乘,两个数组的卷积
a=[1 3 5 7 9];
b=[1 2 4 6 8];
c=conv(a,b)
输出结果如下:
(3)除
c=[2 4 5 2 67 8 3];
b=[2 2 4];
[a,r]=deconv(c,b)
输出结果如下: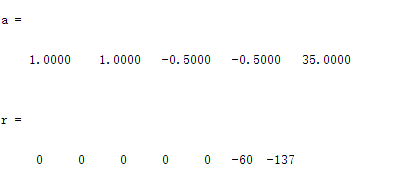
(4)导数
c=[2 4 5 2 67 8 3];
d=polyder(c)
输出结果如下: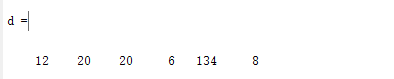
(5)积分
polyint(p,k);其中参数p为多项式积分项的系数,k为多项式的积分常量,对于积分常量,如果为0,这可以在括号中不写参数k。
a=[1 3 5 7 9];
b=polyint(a)
输出结果如下:
比如若要求积分
p=[1 2 3];
a = 1;
b = 4;
A= diff(polyval(polyint(p),[a b]));
输出结果如下: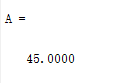
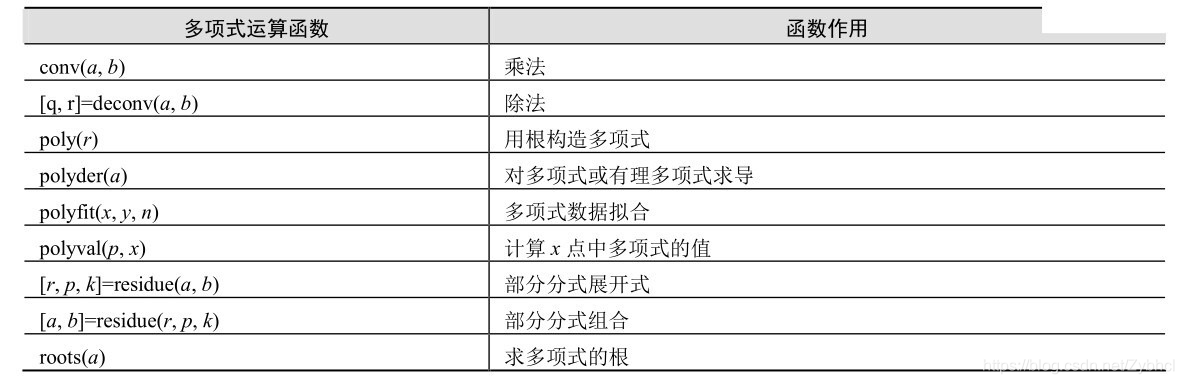
总结: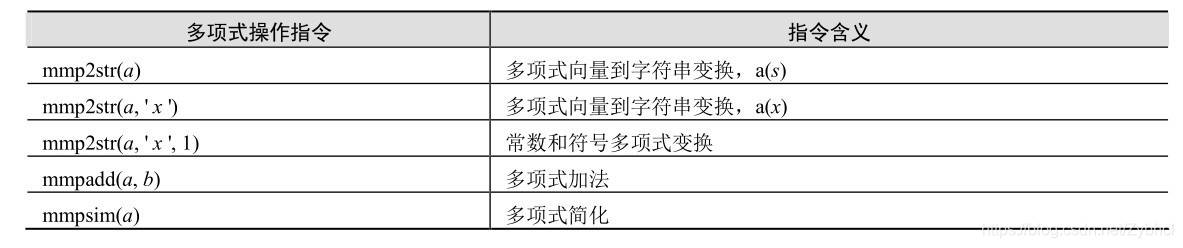
版权声明:本文为Zybhcl原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。