为什么需要分位数回归
======================
■ 此前的模型在估计什么?
* 解释变量 x 对被解释变量 y 的条件期望 E(y|x) 的影响,实际上是 “ 均值回归 ”
■ 我们真正关心的是什么?
* 我们想知道 x 对整个条件分布 y|x 的影响
*
* - 条件期望 E(y|x) 只刻画条件分布 y|x 几种趋势的一个指标而已
* 如果条件分布 y|x 不是对称分布,则条件期望 E(y|x) 很难反映整个条件分布的全貌
*
* - OLS 的古典均值回归,最小化目标函数值未残差平方和
* 容易受极端值的影响
* 如果能够估计出条件分布 y|x 的若干重要的条件分位数
* 就能对条件分布 y|x 有更全面的认识
■ 分位数回归
* Koenker & Bassett() 提出 “ 分位数回归 ” ( Quantile Regression )
* 使用残差绝对值的加权平均作为最小化的目标函数,不容易受极端值影响
* 因此较为稳健(这一点很重要!!!)
* 更重要的是,分位数回归能够提供关于条件分布 y|x 的全面信息
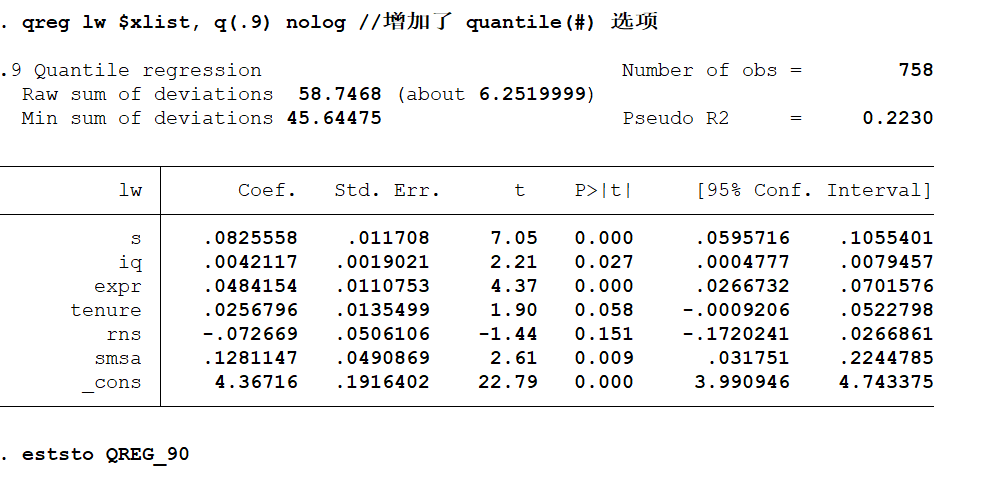
■ 如何理解分位数回归结果?
* 不同的 y 区间内, x 对 y 的影响作用
*
* 正确的例子:
* 我们想知道教育如何影响工资收入,进行分位数回归
* 此时教育投资是 x ,工资收入是 y
* 将 y 分成低 - 中 - 高三个区间,发现教育投资对中等收入群体的收入提升作用明显
* 低 - 高区间的影响不明显
- [ 怎么解释?]
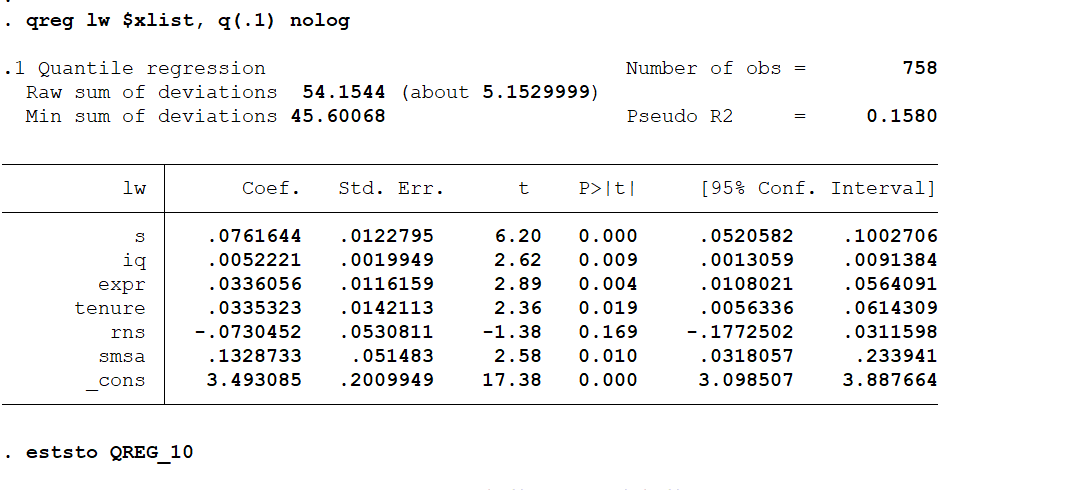
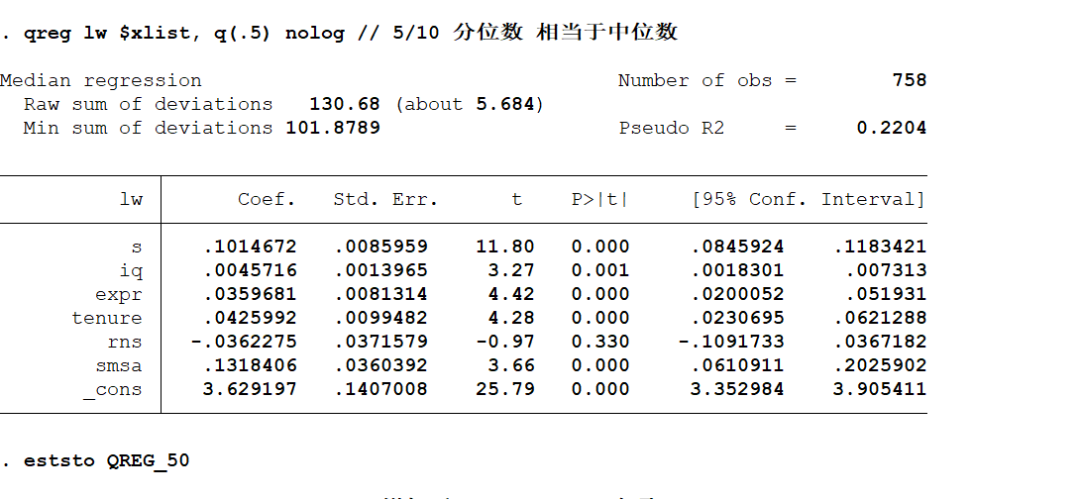
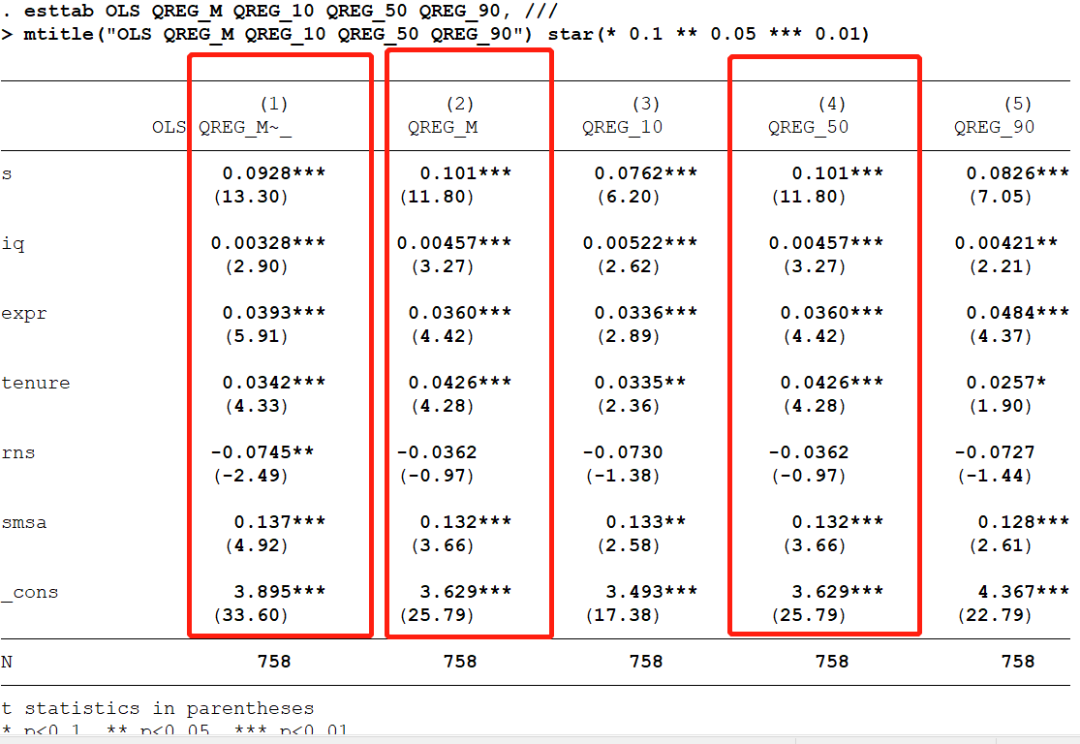
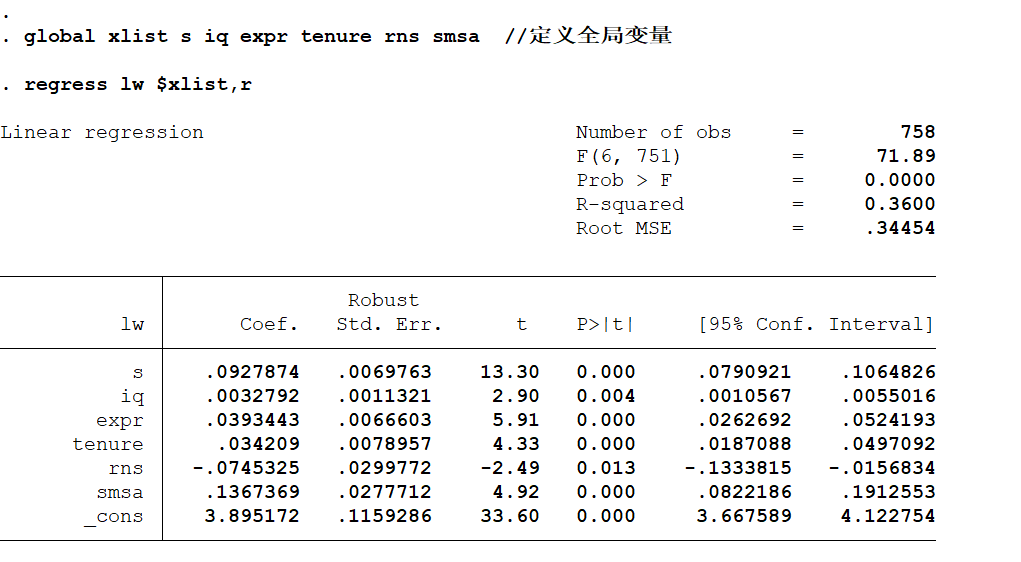
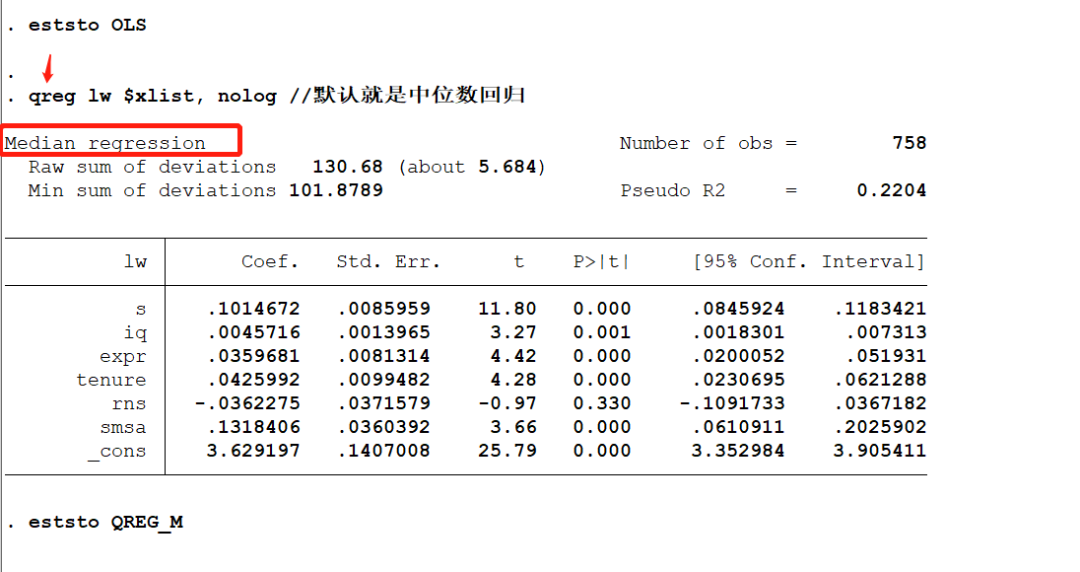
* 核心变量 s 的系数是 0.1015 ,通过 1% 的显著性检验
* 说明增加 1 年教育( s )能够使工资的中位数增加 10.15%
对比 OLS 结果, s 对 lw 中位数的影响比平均影响大一点