【算法图解】第七章：7.5（狄克斯特拉算法完整代码）

以下为我整理的狄克斯特拉算法完整代码请大家指正（经过测试练习亦通过）

# 这里的参数理论上可以只传图对应的散列表，起始通过key值来确定costs和parents，时间原因这里先不优化
def solution(costs, parents, graph): 
    processed = []  # 定义列表记录已计算开销的节点
    node = find_lowest_cost_node(costs=costs, processed=processed)  # 调用函数找到消费散列表中开销最小但未计算开销的节点
    while node is not None:  # 循环结束的条件为计算完所有的节点
        cost = costs[node]  # 获取消费散列表中当前节点已消费的值
        neighbors = graph[node]  # 获取到该节点的所有的邻居
        for n in neighbors.keys():
            new_cost = cost + neighbors[n]  # 计算该节点到邻居总共需要消费多少
            if costs[n] > new_cost:  # 如果当前消费散列表中邻居节点消费大于该节点到邻居节点所消费
                costs[n] = new_cost  # 更新当前消费散列表中邻居节点消费
                parents[n] = node  # 更新始终关系散列表中邻居节点的父节点为该节点
        processed.append(node)  # 将计算了消费的节点存入记录列表中
        node = find_lowest_cost_node(costs=costs, processed=processed)  # 调用函数找到消费散列表中开销最小但未计算开销的节点
    return costs, parents, processed


def find_lowest_cost_node(costs, processed):
    lowest_cost = float('inf')
    lowest_cost_node = None
    for node in costs:
        cost = costs[node]
        if cost < lowest_cost and node not in processed:
            lowest_cost = cost
            lowest_cost_node = node
    return lowest_cost_node


if __name__ == '__main__':
    graph = {'start': {'a': 6, 'b': 2}, 'a': {'end': 1}, 'b': {'a': 3, 'end': 5}, 'end': {}}
    parents = {'a': 'start', 'b': 'start', 'end': None}
    costs = {'a': 6, 'b': 2, 'end': float('inf')}
    for x in solution(graph=graph, costs=costs, parents=parents):
    	print(x)

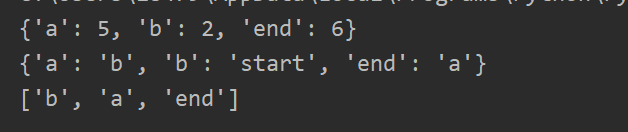
以下为执行结果