概念:
杨辉三角形,又称贾宪三角形,帕斯卡三角形,是二项式系数在三角形中的一种几何排列。

分析:
我们把上图三角形左边的空格去掉后进行分析:

观察上图可以发现:
1、上图三角形的第一列的每个元素都是1;
2、三角形的斜边每个元素都是1;
3、从第三行,第二列开始,三角形中间的每个元素的值都等于它上面两个元素的和。

思路:
我们可以把这个杨辉三角看成一个二维数组,而我们只需要打印这个数组的左下方部分 :

1、我们首先创建一个二维数组:
#define ROW 10
#define COL 10
int main()
{
int arr[ROW][COL] = { 0 };
return 0;
}2、这个二维数组的第一列的元素都为1,即当COL==0时,arr[ROW][COL] = 1;
3、这个二维数组的对角线的元素都为1,即当ROW == COL时,arr[ROW][COL] = 1;
4、从第三行,第二列开始,数组中间的每个元素的值都等于它上面两个元素的和:
当(ROW>=2 && COL >=1)时,arr[ROW][COL] = arr[ROW - 1][COL - 1] + arr[ROW - 1][COL];
以上内容转换为代码:
#define ROW 10
#define COL 10
int main()
{
int arr[ROW][COL] = { 0 };
int i = 0;
int j = 0;
//第一列和对角线都为1
for (i = 0;i < ROW;i++)
{
for (j = 0;j <= i;j++)
{
if (j == 0)//第一列为1
{
arr[i][j] = 1;
}
if (i == j)//对角线为1
{
arr[i][j] = 1;
}
//从第三行,第一列的元素开始,中间的每个元素都等于它上面的两个元素之和
if (i >= 2 && j >= 1)
{
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
}
}
return 0;
}打印:
打印时,只需要再遍历一次数组左下方的元素即可:
for (i = 0;i < ROW;i++)
{
for (j = 0;j <= i;j++)
{
printf("%-3d ", arr[i][j]);
}
printf("\n");//打印完一行后换行
}效果如下:

如果想打印出刚开始的等腰三角形那种情况,只需要再控制一下每一行前面的空格数量,我们再次观察一下第一个图中杨辉三角的前三行:
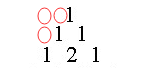
当行号为3时,第一行有2个空格(ROW-1),第二行有1个空格(ROW-2),第三行有0个空格(ROW-3)
转换为代码:
for (i = 0;i < ROW;i++)
{
for (j = 0;j < (ROW - 1) - i;j++)//控制空格数量
{
printf(" ");
}
for (j = 0;j <= i;j++)
{
printf("%-3d ", arr[i][j]);
}
printf("\n");//打印完一行后换行
}因为 i 的初始值为0,所以循环条件中需要先给ROW - 1,然后再减 i 。
效果如下:

所有代码:
最后是整个程序的所有代码:
#include <stdio.h>
#define ROW 10
#define COL 10
int main()
{
int arr[ROW][COL] = { 0 };
int i = 0;
int j = 0;
//第一列和对角线都为1
for (i = 0;i < ROW;i++)
{
for (j = 0;j <= i;j++)
{
if (j == 0)//第一列为1
{
arr[i][j] = 1;
}
if (i == j)//对角线为1
{
arr[i][j] = 1;
}
//从第三行,第一列的元素开始,中间的每个元素都等于它上面的两个元素之和
if (i >= 2 && j >= 1)
{
arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
}
}
}
for (i = 0;i < ROW;i++)
{
for (j = 0;j < (ROW - 1) - i;j++)//控制空格数量
{
printf(" ");
}
for (j = 0;j <= i;j++)
{
printf("%-3d ", arr[i][j]);
}
printf("\n");//打印完一行后换行
}
return 0;
}版权声明:本文为m0_67683346原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。