模式识别学习笔记——第2章 统计学习方法—2.3最小风险贝叶斯决策

根据场合的不同，我们的决策可能不仅仅是错误率，还有可能是决策错误带来的风险。所谓最小风险贝叶斯决策，就是考虑各种错误造成损失不同时的一种最优决策。

下面用决策论的数学符号表示最小风险贝叶斯决策问题：

把样本\vec{x}看作是由d个特征成员组成的d维随机向量x=[x_1, x_2, ...,x_d]^T

状态空间\Omega =\{w_1,w_2,...,w_c\}

对随机向量\vec{x}可采取的决策组成了决策空间，它由k个决策组成A=\{a_1,a_2,...,a_k\}

值得注意的是，状态空间和决策空间不一定是一一对应的，即不一定有k=c。什么意思呢？比如，有时除了将样本\vec{x}决策为某一类别，还可能对一些样本\vec{x}做出拒绝的决策；有时亦可能在决策时把几类合并成为同一个大类；等多种情况。

设对于实际状态为w_j的样本\vec{x}，采取决策a_i所带来的损失记为：

\lambda (a_i,w_j),\quad i=1,...,k, \quad j=1,...,c

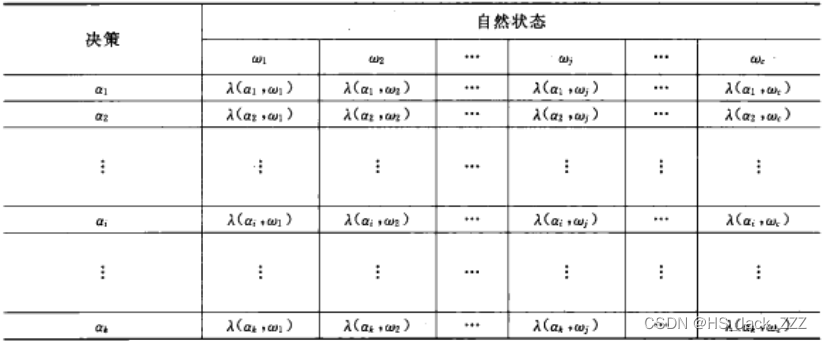
上式称作损失函数。通常用表格形式给出，也称决策表：

图片截至《模式识别（第三版）》决策表

决策表是需要人为确定的，决策表不同会导致决策结果的不同。因此，在实际应用中，需要认真分析所研究问题的内在特点和分类的目的，与应用领域的专家共同设计出适当的决策表，才能保证模式识别发挥有效作用。

对于某个样本\vec{x}，对它采取决策a_i的期望损失是：

R(a_i|\vec{x})=E[\lambda(a_i,w_j)|\vec{x}]=\sum_{j=1}^{c}\lambda(a_i,w_j)p(w_j|\vec{x})\quad i=1,...,k

如果对概率论不太熟悉，可以参照下面这个离散的条件期望公式：

E(X|Y=y)=\sum_{x} xP(x|y)

设有一个决策规则a(x)，这个函数对特征空间中所有的样本\vec{x}采取决策所造成的期望损失是：

R(a)=\int R(a(\vec{x})|\vec{x})p(\vec{x})d\vec{x}

 R(a)称作平均风险或期望风险。最小化风险贝叶斯决策就是最小化这一期望风险，即

min_a{R(a)}

可以看出p(\vec{x})已知，是一个定值，不需要关注。要使积分最小，那么就应该让函数a(\vec{x})在定义域内使得R(a(\vec{x})|\vec{x})最小。

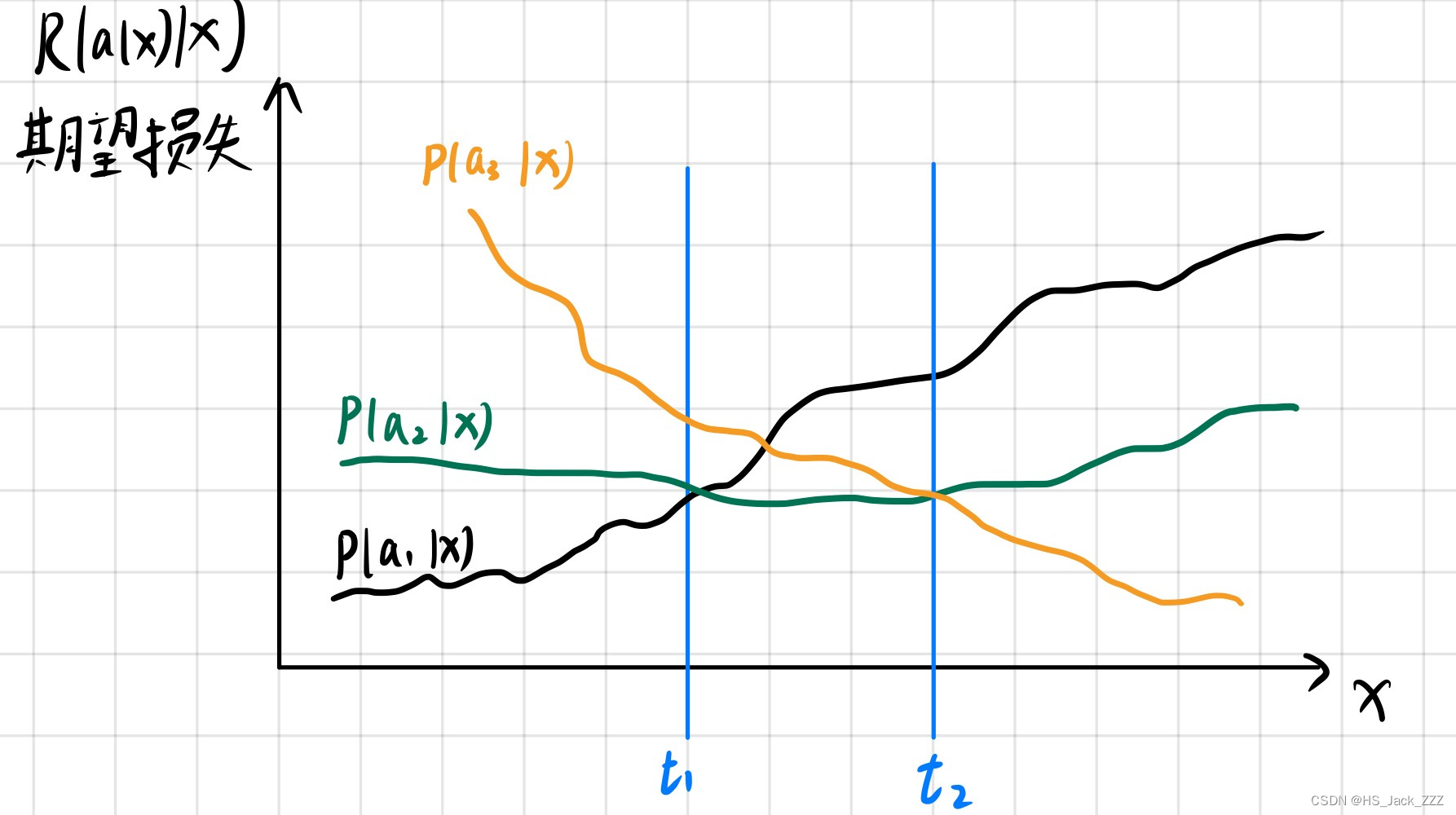
有了上面这张图就会好理解很多，这张图的样本是一个一维的x，这样比较好理解。很坐标是所有样本值，纵坐标是期望损失。范围在0到t_1 ，有三种决策，很容易得出决策a_1期望损失最小，因此此时应该使用决策a_1。最小风险贝叶斯决策就是

若R(a_i|\vec{x})=minR(a_j|\vec{x}) \quad j=1,...,k，则a=a_i

理论说完之后，就要应用在实际问题之中。我们可以按照以下步骤计算：

利用贝叶斯公式计算后验概率p(w_i|x)

利用决策表，计算期望损失（条件风险）

R(a_i|\vec{x})=E[\lambda(a_i,w_j)|\vec{x}]=\sum_{j=1}^{c}\lambda(a_i,w_j)p(w_j|\vec{x})\quad i=1,...,k

 在各种决策中选择风险最小的决策，即：

a=argminR(a_i|x)

版权声明：本文为HS_Jack_ZZZ原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。