【leetcode】91. Decode Ways

题目：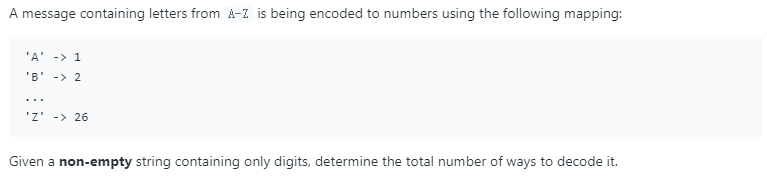

思路：
直观思路就是递归求解，我测试了几个用例，是正确的，但是超时了。
所以采用动态规划的方法。dp[i]表示到第i元素（包括第i元素）为止，所有可能出现的组合情况的统计。 当遇到0的时候，就稍微麻烦了一点，我绕了半天才绕过来的。

• 情况1： 假设当前元素为第i个元素。当第i+1个元素为0时，就不能将dp[i]加到dp[i+1]上。如果你将dp[i]加到dp[i+1]上，你就默认了单独第i+1个元素（值为0）是可以被解码的，但这是错的，单独0是无法被解码的，没有对应的编解码映射关系。所以，如果第i+1个元素为0时，则不能将dp[i]加到dp[i+1]上。
• 情况2： 假设当前元素为第i个元素。如果接下来的连续两个字符（第i+1个元素和第i+2个元素）能够被解码（单独写个check函数检查下就好），那么dp[i]就可以加到dp[i+2]上。
• 提醒一下： 当前元素的值是否为0是无所谓的，不需要管当前值是啥，因为当前值的来源有两个途径，就是来自情况1和情况2。当前元素为0与非0的情况无任何区别。关键是情况1和情况2考虑好就行。

代码实现：

class Solution {
public:
    bool check(char a, char b){
        if (a == '0' || a > '2'){
            return false;
        }
        if (a == '2' && b > '6'){
            return false;
        }
        
        return true;
    }
    
    int numDecodings(string s) {
        if (s.size() <= 0 || s[0] == '0'){
            return 0;
        }
        if (s.size() == 1){
            return 1;
        }
        
        vector<int> dp(s.size(), 0);
        dp[0] = 1;
        if (check(s[0],s[1])){
            dp[1] = 1;
        }
        int i = 0;
        while (i < s.size()-1){
            if (i+1 < s.size() && s[i+1] != '0'){
                dp[i+1] += dp[i];
            }
            if (i+2 < s.size() && check(s[i+1],s[i+2])){
                dp[i+2] += dp[i];
            }
            ++i;
        }
        
        return dp[dp.size()-1];
    }
};

discuss:
思路：倒着用动态规划。公式是dp[i] = dp[i+1] + dp[i+2]。示意图如下。

class Solution {
public:
    int numDecodings(string s) {
        int n = s.size();
        vector<int> dp(n+1);
        dp[n] = 1;
        
        for (int i = n - 1; i >= 0; --i){ // 倒着求，dp[i] = dp[i+1] + dp[i+2]的方式求
            if (s[i] == '0')
                dp[i] = 0;
            else {
                dp[i] = dp[i+1];
                if (i < n - 1 && (s[i] == '1' || s[i] == '2' && s[i+1] < '7'))
                    dp[i] += dp[i+2];
            }
        }
        
        return s.empty() ? 0 : dp[0];
    }
    
};