基础理论
广泛使用各种不同的采样一致性参数估计算法用于排除错误的样本,样本不同对应的应用不同,例如剔除错误的配准点对,分割出处在模型上的点集等。PCL 中以随机采样一致性算法( RANSAC) 为核心,实现了五种类似于RANSAC的随机参数估计算法,例如随机采样一致性估计(RANSAC ) 、最大似然一致性估计 (MLESAC ) 、最小中值方差一致性估计 ( LMEDS )等,所有的估计参数算法都符合一致性准则。利用RANSAC可以实现点云分割,在PCL中设计的采样一致性算法的应用主要就是对点云进行分割,根据设定的不同的几个模型,估计对应的几何参数模型的参数,在一定容许的范围内分割出在模型上的点云。目前 PCL 中支持的几何模型分割有空间平面、直线、二维或三维圆、圆球、锥体等 。 RANSAC的另一应用就是点云的配准对的剔除。
引入原因
模型拟合常用的方法有Least Square、Hough Transform、RANSAC。最小二乘受离群点的影响比较大,霍夫变换不适用于复杂模型。RANSAC 与通常的数据最佳拟合技术相反,不是用尽可能多的数据点去获得模型的估计,而是用尽可能少的可行数据并尽量地扩大一致性数据集。RANSAC在实际应用中的效果很好。
RANSAC算法详解
随机采样一致算法是从一组包含离群的被观测数据中估算出数学模型参数的迭代算法。RANSAC算法是一种不确定算法,它只能在一种概率下产生结果,并且这个概率会随着迭代次数的增加而加大。
具体实现过程
1、RANSAC从样本中随机抽选出一个样本子集
2、使用最小方差估计算法对这个子集计算模型参数
3、计算所有样本与该模型的偏差
4、使用一个预先设定好的阀值与偏差比较(当偏差小于阂值时,该样本点属于模型内样本点(inliers),简称局内点或内点,否则为模型外样本点,简称局外点或外点)
5、记录下当前的inliers的个数,然后重复这一过程
6、每一次重复都记录当前最佳的模型参数(所谓最佳即是inliers的个数最多,此时对应的inliers个数为best_ ninliers)
7、计算一个迭代结束评判因子,据此决定是否迭代结束(每次迭代的末尾都会根据期望的误差率、best_ninliers ,总样本个数、当前迭代次数,计算一 个迭代结束评判因子,据此决定是否迭代结束。
8、迭代结束后,最佳模型参数就是最终的模型参数估计值。
直线拟合
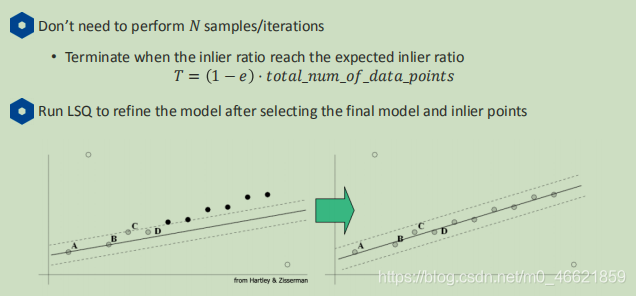
 • 距离的临界值r通常通过经验进行选择
• 距离的临界值r通常通过经验进行选择
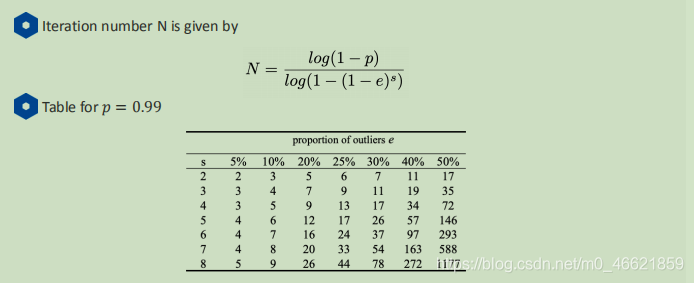
• 迭代的次数N的选择标准是迭代到至少有一个随机选择的样本以概率p不包含异常值,停止迭代

代码
import numpy as np
import matplotlib.pyplot as plt
import random
import math
#产生二维数据
size = 50
X = np.linspace(0, 10, size)
Y = 2 * X + 8
#让散点图的数据更加随机并添加一些噪音
random_x = []
random_y = []
#添加直线随机噪声
for i in range(size):
random_x.append(X[i] + random.uniform(-0.5, 0.5))
random_y.append(Y[i] + random.uniform(-0.5, 0.5))
#添加随机噪声
for i in range(size):
random_x.append(random.uniform(0, 10))
random_y.append(random.uniform(10, 40))
RANDOM_X = np.array(random_x) #散点图的横轴
RANDOM_Y = np.array(random_y) #散点图的纵轴
#画散点图
fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)
ax1.set_title("RANSAC")
ax1.scatter(RANDOM_X, RANDOM_Y)
ax1.set_xlabel("x")
ax1.set_ylabel("y")
#使用RANSAC算法估算模型
N_iters = 100000
tao = 0.25
p = 0.99
best_k = 0
best_b = 0
pretotal = 0
for i in range(N_iters):
#在所有数据中随机选择两个点
sample_index = random.sample(range(size * 2), 2)
x_1 = RANDOM_X[sample_index[0]]
x_2 = RANDOM_X[sample_index[1]]
y_1 = RANDOM_Y[sample_index[0]]
y_2 = RANDOM_Y[sample_index[1]]
k = (y_2 - y_1) / (x_2 - x_1)
b = y_1 - k * x_1
total_inlier = 0
for index in range(size * 2):
y_estimate = k * RANDOM_X[index] + b
if abs(y_estimate - RANDOM_Y[index]) < tao:
total_inlier = total_inlier + 1
#判断当前模型是否比之前估算的模型好
if total_inlier > pretotal:
N_iters = math.log(1 - p)/math.log(1 - pow(total_inlier / (size * 2), 2))
pretotal = total_inlier
best_k = k
best_b = b
#判断是否当前模型已经符合超过一半的点
if total_inlier > size:
break
#用得到的最佳估计画图
Y = best_k * RANDOM_X + best_b
ax1.plot(RANDOM_X, Y)
text = "best_k = " + str(best_k) + "\nbest_b = " + str(best_b)
plt.text(5, 10, text, fontdict = {'size': 8, 'color': 'r'})
plt.show()
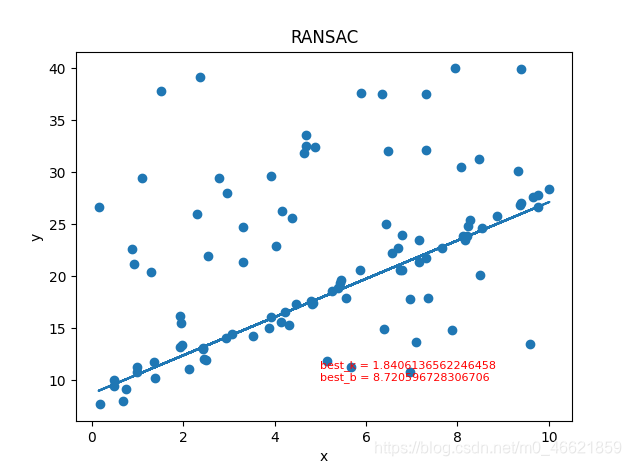
实现结果
平面拟合
1、从点云中随机选取三个点。
2、由这三个点组成一个平面。
3、计算所有其他点到该平面的距离,如果小于阈值T,就认为是处在同一个平面的点。
4、如果处在同一个平面的点超过n个,就保存下这个平面,并将处在这个平面上的点都标记为已匹配。
5、终止的条件是迭代N次后找到的平面小于n个点,或者找不到三个未标记的点。
代码
import numpy as np
from ransac import *
import random
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
def augment(xyzs):
axyz = np.ones((len(xyzs), 4))
axyz[:, :3] = xyzs
return axyz
def estimate(xyzs):
axyz = augment(xyzs[:3])
return np.linalg.svd(axyz)[-1][-1, :]
def is_inlier(coeffs, xyz, threshold):
return np.abs(coeffs.dot(augment([xyz]).T)) < threshold
def run_ransac(data, estimate, is_inlier, sample_size, goal_inliers, max_iterations, stop_at_goal=True, random_seed=None):
best_ic = 0
best_model = None
random.seed(random_seed)
# random.sample cannot deal with "data" being a numpy array
data = list(data)
for i in range(max_iterations):
s = random.sample(data, int(sample_size))
m = estimate(s)
ic = 0
for j in range(len(data)):
if is_inlier(m, data[j]):
ic += 1
print(s)
print('estimate:', m,)
print('# inliers:', ic)
if ic > best_ic:
best_ic = ic
best_model = m
if ic > goal_inliers and stop_at_goal:
break
print('took iterations:', i+1, 'best model:', best_model, 'explains:', best_ic)
return best_model, best_ic
if __name__ == '__main__':
fig = plt.figure()
ax = mplot3d.Axes3D(fig)
def plot_plane(a, b, c, d):
xx, yy = np.mgrid[:10, :10]
return xx, yy, (-d - a * xx - b * yy) / c
n = 100
max_iterations = 100
goal_inliers = n * 0.3
# test data
xyzs = np.random.random((n, 3)) * 10
xyzs[:50, 2:] = xyzs[:50, :1]
ax.scatter3D(xyzs.T[0], xyzs.T[1], xyzs.T[2])
# RANSAC
m, b = run_ransac(xyzs, estimate, lambda x, y: is_inlier(x, y, 0.01), 3, goal_inliers, max_iterations)
a, b, c, d = m
xx, yy, zz = plot_plane(a, b, c, d)
ax.plot_surface(xx, yy, zz, color=(0, 1, 0, 0.5))
plt.show()
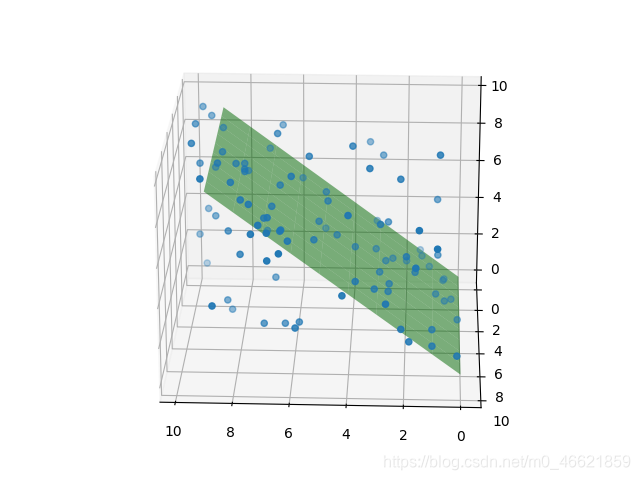
结果显示
实例
import open3d as o3d
import numpy as np
import random
import math
import sys
#可视化覆铜板并进行渲染
pcd = o3d.io.read_point_cloud("data.ply")
o3d.visualization.draw_geometries([pcd])
#体素大小为0.01时降采样
voxel_down_pcd = pcd.voxel_down_sample(voxel_size=0.01)
def display_inlier_outlier(cloud, ind):
global inlier_cloud
global points
global inlier_data
inlier_cloud = cloud.select_by_index(ind)
cl, ind = voxel_down_pcd.remove_statistical_outlier(nb_neighbors=20, std_ratio=2.0)
display_inlier_outlier(voxel_down_pcd, ind)
#用最小二乘和ransac拟合平面
def PlaneLeastSquare(X):
#z=ax+by+c,return a,b,c
A=X.copy()
b=np.expand_dims(X[:,2],axis=1)
A[:,2]=1
#通过X=(AT*A)-1*AT*b直接求解
A_T = A.T
A1 = np.dot(A_T,A)
A2 = np.linalg.inv(A1)
A3 = np.dot(A2,A_T)
x= np.dot(A3, b)
return x
def PlaneRANSAC(X,tao,e=0.4,N_regular=100):
#return plane ids
s = X.shape[0]
count = 0
p = 0.99
dic = {}
#确定迭代次数
if math.log(1-(1-e)**s)<sys.float_info.min:
N = N_regular
else:
N = math.log(1-p)/math.log(1-(1-e)**s)
#开始迭代
while count < N:
ids = random.sample(range(0,s),3)
p1,p2,p3 = X[ids]
#判断是否共线
L = p1 - p2
R = p2 - p3
if 0 in L or 0 in R:
continue
else:
if L[0]/R[0] == L[1]/R[1] == L[2]/R[2]:
continue
#计算平面参数
a = (p2[1] - p1[1]) * (p3[2] - p1[2]) - (p2[2] - p1[2]) * (p3[1] - p1[1]);
b = (p2[2] - p1[2]) * (p3[0] - p1[0]) - (p2[0] - p1[0]) * (p3[2] - p1[2]);
c = (p2[0] - p1[0])*(p3[1] - p1[1]) - (p2[1] - p1[1])*(p3[0] - p1[0]);
d = 0 - (a * p1[0] + b*p1[1] + c*p1[2]);
dis=abs(a*X[:,0]+b*X[:,1]+c*X[:,2]+d)/(a**2+b**2+c**2)**0.5
idset=[]
for i ,d in enumerate(dis):
if d <tao:
idset.append(i)
#再使用最小二乘法
p=PlaneLeastSquare(X[idset])
a,b,c,d=p[0],p[1],-1,p[2]
dic[len(idset)]=[a,b,c,d]
if len(idset)>s*(1-e):
break
count+=1
#通过包含最多内点的模型为最优模型
parm=dic[max(dic.keys())]
parm1=dic[min(dic.keys())]
a2,b2,c2,d2=parm
a1,b1,c1,d1=parm1
dis=abs(a2*X[:,0]+b2*X[:,1]+c2*X[:,2]+d2)/(a2**2+b2**2+c2**2)**0.5
dis1=abs(a1*X[:,0]+b1*X[:,1]+c1*X[:,2]+d1)/(a1**2+b1**2+c1**2)**0.5
#求最优模型的标准误差(精度)
idset=[]
idset1=[]
valueset=[]
valueset1=[]
for i ,d in enumerate(dis):
if d <tao:
idset.append(i)
valueset.append(d)
for i1 ,d1 in enumerate(dis1):
if d1 <tao:
idset1.append(i1)
valueset1.append(d1)
value_std = np.std(valueset)
value_std1 = np.std(valueset1)
#打印最优迭代轮次的标准误差(精度)
print(parm,value_std)
print(parm1,value_std1)
#返回平面上点的索引
return np.array(idset)
#找出平面点
inlier_data = np.asarray(inlier_cloud.points)
planeids=PlaneRANSAC(inlier_data,0.01)
planedata=inlier_data[planeids]
planepcd = o3d.geometry.PointCloud()
planepcd.points = o3d.utility.Vector3dVector(planedata)
#找出平面外的点
othersids=[]
for i in range(inlier_data.shape[0]):
if i not in planeids:
othersids.append(i)
otherdata=inlier_data[othersids]
otherpcd = o3d.geometry.PointCloud()
otherpcd.points = o3d.utility.Vector3dVector(otherdata)
o3d.visualization.draw_geometries([planepcd]) #显示平面点
o3d.visualization.draw_geometries([otherpcd]) #显示平面外的点
结果显示

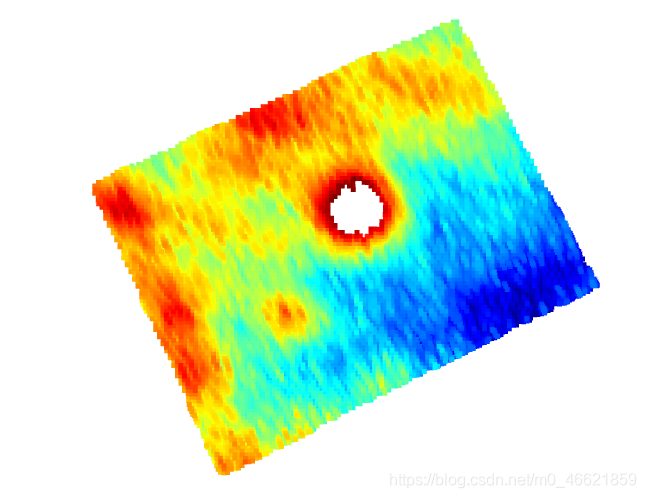
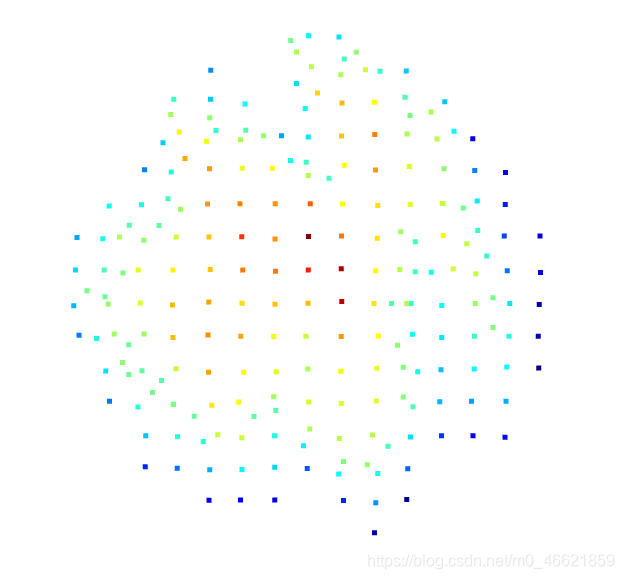
PCL代码
#include <iostream> //标准的输入输出头文件
#include <pcl/console/parse.h> //解析头文件
#include <pcl/filters/extract_indices.h> //索引提取滤波类头文件
#include <pcl/io/pcd_io.h> //PCD读写类相关的头文件
#include <pcl/point_types.h> //点类型定义头文件
#include <pcl/sample_consensus/ransac.h> //随机采样一致性头文件
#include <pcl/sample_consensus/sac_model_plane.h> //平面拟合头文件
#include <pcl/sample_consensus/sac_model_sphere.h> //球面拟合头文件
#include <pcl/visualization/pcl_visualizer.h> //可视化头文件
#include <boost/thread/thread.hpp> //线程模板
boost::shared_ptr<pcl::visualization::PCLVisualizer> simpleVis (pcl::PointCloud<pcl::PointXYZ>::ConstPtr cloud)
{
//打开一个3D视窗并添加点云
boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer (new pcl::visualization::PCLVisualizer ("3D Viewer")); //创建视窗对象
viewer->setBackgroundColor(0, 0, 0); //设置视窗背景为黑色
viewer->addPointCloud<pcl::PointXYZ>(cloud, "sample cloud"); //添加点云
viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 3, "sample cloud"); //设置点云显示的尺寸
viewer->addCoordinateSystem(1.0); //添加坐标系
viewer->initCameraParameters();
return(viewer);
int main(int argc, char** argv)
{
srand(time(NULL)); //初始化系统时间
//生成点云
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
pcl::PointCloud<pcl::PointXYZ>::Ptr final (new pcl::PointCloud<pcl::PointXYZ>);
cloud->width = 5000; //设置点云数目
cloud->height = 1; //设置为无序点云
cloud->is_dense = false;
cloud->point.resize(cloud->width * cloud->height);
srand(time(NULL));
pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
pcl::PointCloud<pcl::PointXYZ>::Ptr final (new pcl::PointCloud<pcl::PointXYZ>);
cloud->width = 5000;
cloud->height = 1;
cloud->is_dense = false;
cloud->points.resize(cloud->width * cloud->height);
for (size_t i = 0; i < cloud->points.size(); ++i)
{
if (pcl::console::find_argument(argc, argv, "-s") >= 0 || pcl::console::find_argument(argc, argv, "-sf") >= 0)
{
///根据命令行参数,用x^2 + y^2 + z^2 = 1 设置一部分点云数据
cloud->points[i].x = 1024 * rand() / (RAND_MAX + 1.0f);
cloud->points[i].y = 1024 * rand() / (RAND_MAX + 1.0f);
if (i % 5 == 0)
cloud->points[i].z = 1024 * rand() / (RAND_MAX + 1.0f); //此处是局外点
else if (i % 2 == 0)
cloud->points[i].z = sqrt(1 - (cloud->points[i].x * cloud->points[i].x) - (cloud->points[i].y * cloud->points[i].y));
else
cloud->points[i].z = - sqrt(1 - (cloud->points[i].x * cloud->points[i].x) - (cloud->points[i].y * cloud->points[i].y));
}
else
{
///根据命令行参数,用x + y + z = 1,设置一部分点云数据
cloud->points[i].x = 1024 * rand() / (RAND_MAX + 1.0f);
cloud->points[i].y = 1024 * rand() / (RAND_MAX + 1.0f);
if (i % 5 == 0)
cloud->points[i].z = 1024 * rand() / (RAND_MAX + 1.0f); //此处是局外点
else
cloud->points[i].z = -1 * (cloud->points[i].x + cloud->points[i].y);
}
}
std::vector<int> inliers; //存储局内点集合的点的索引的整数型向量
//创建随机采样一致性对象
pcl::SampleConsensusModelSphere<pcl::PointXYZ>::Ptr model_s (new pcl::SampleConsensusModelSphere<pcl::PointXYZ> (cloud)); //针对球模型的对象
pcl::SampleConsensusModelPlane<pcl::PointXYZ>::Ptr model_p (new pcl::SampleConsensusModelPlane<pcl::PointXYZ> (cloud)); //针对平面模型的对象
if (pcl::console::find_argument(argc, argv, "-f") >= 0)
{
//根据命令行参数,来随机估算对应的平面模型,并存储估计的局内点
pcl::RandomSampleConsensus<pcl::PointXYZ> ransac(model_p);
ransac.setDistanceThreshold(0.01); //与平面距离小于0.01的点作为局内点
ransac.computeModel(); //执行随机参数运算
ransac.getInliers(inliers); //存储估计所得的局内点
}
else if (pcl::console::find_argument(argc, argv, "-sf") >= 0)
{
//根据命令行参数,来随机估算对应的圆球模型,并存储估计的局内点
pcl::RandomSampleConsensus<pcl::PointXYZ> ransac (model_s);
ransac.setDistanceThreshold(0.01); //与球面距离小于0.01的点作为局内点考虑
ransac.computeModel(); //执行随机参数估计
ransac.getInliers(inliers); //存储估计所得的局内点
}
pcl::copyPointCloud<pcl::PointXYZ>(*cloud, inliers, *final); //复制估算模型的所有局内点到final中
boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer; //创建可视化对象
if (pcl::console::find_argument(argc, argv, "-f") >= 0 || pcl::console::find_argument(argc, argv, "-sf") >= 0 )
viewer = simpleVis(final); //加入局内点
else
viewer = simpleVis(cloud); //加入原始点云
while(!viewer->wasStopped())
{
//每次调用spinOnce都给视窗处理事件的时间,这样允许鼠标和键盘等交互操作
viewer->spinOnce(100);
boost::this_thread::sleep(boost::posix_time::microseconds(100000));
}
return(0);
}
实现效果
 显示的点云包含球面上的点集和噪声点
显示的点云包含球面上的点集和噪声点
 显示的局内点只包含球面上的点集
显示的局内点只包含球面上的点集
 显示创建的原始点云(包含局内点和局外点),噪声点呈立方体状,主要是因为创建点云时利用的随机数只产生在(0,1)范围内。
显示创建的原始点云(包含局内点和局外点),噪声点呈立方体状,主要是因为创建点云时利用的随机数只产生在(0,1)范围内。
 显示的局内点只包含平面上的点集
显示的局内点只包含平面上的点集
知识补充
