课程设计：简单计算器的实现

一.设计目标

通过MFC应用程序创建基于对话框的简单计算器， 利用设计的按钮控件输入并实现算数表达式的运算（加、减、乘、除及括号），使表达式与运算结果在编辑框中显示，并保存历史记录。

二.算法思想

1、中缀表达式转成后缀表达式

（后缀表达式队列：postQueue，用于存储逆波兰表达式)
（操作符栈：opStack，对用户输入的操作符进行处理，用于存储运算符）

从左向右依次读取算术表达式的元素X，分以下情况进行不同的处理：
（1）如果X是操作数，直接入队
（2）如果X是运算符，再分以下情况：
a）如果栈为空，直接入栈。
b）如果X==”（“，直接入栈。
c）如果X==”）“，则将栈里的元素逐个出栈，并入队到后缀表达式队列中，直到第一个配对的”(”出栈。（注：“(”和“)”都不 入队）
d）如果是其他操作符（+ - * /）,则和栈顶元素进行比较优先级。 如果栈顶元素的优先级大于等于X，则出栈并把栈中弹出的元素入队，直到栈顶元素的优先级小于X或者栈为空。弹出完这些元素后，才将遇到的操作符压入到栈中。
(3)最后将栈中剩余的操作符全部入队。

2、后缀表达式的计算

（先准备一个栈Res_Stack，用于存放计算的中间过程的值和最终结果）

（1）从左开始向右遍历后缀表达式的元素。
（2）如果取到的元素是操作数，直接入栈Res_Stack，如果是运算符，从栈中弹出2个数进行运算，然后把运算结果入栈
（3）当遍历完后缀表达式时，计算结果就保存在栈里了。

三.编程环境

Visual Studio 2019

四.图形界面的使用

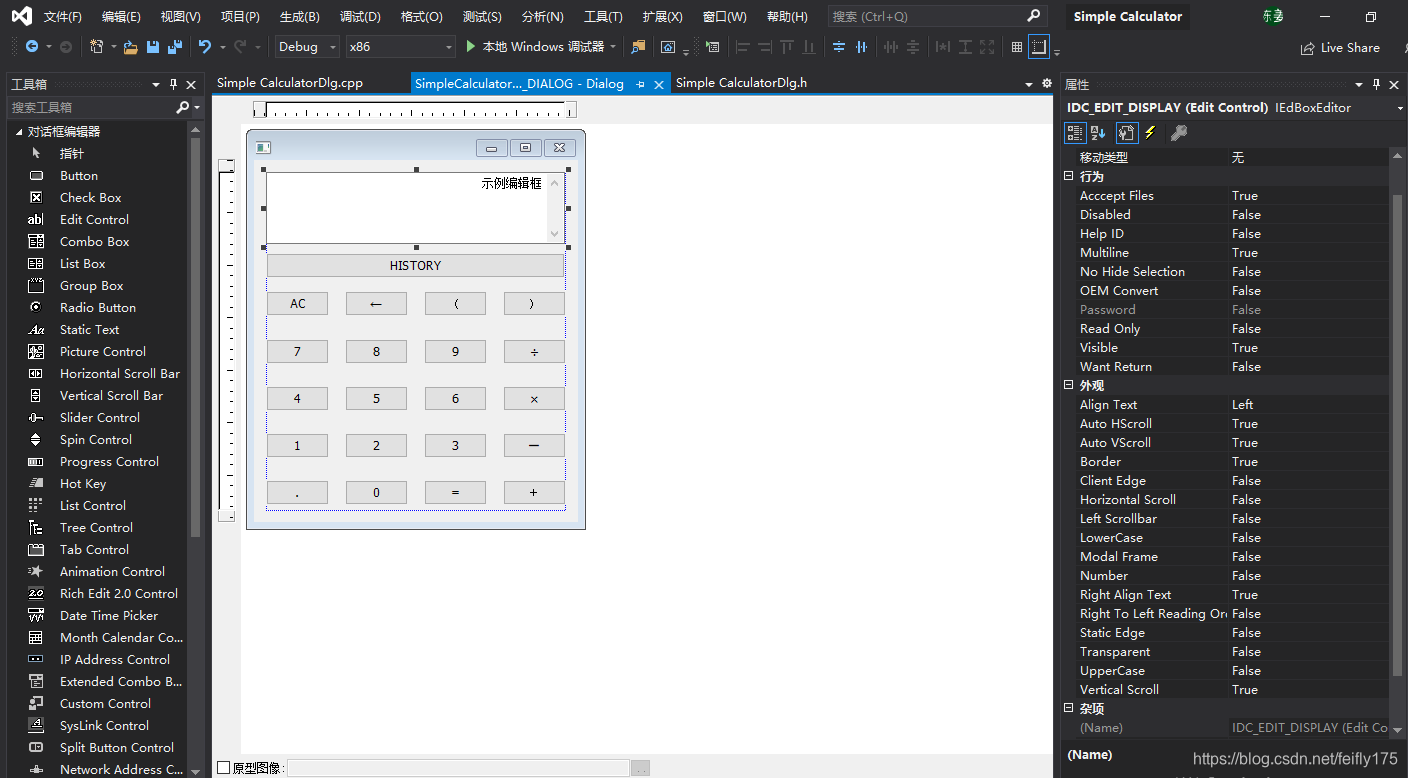
1.控件的使用

在工具箱中拖动所需要的控件，如按钮和编辑框等，然后右击设置控件属性，例如ID的更改。

多行先显示时，先将Multiline设为true，添加垂直滚动条Vertical scroll。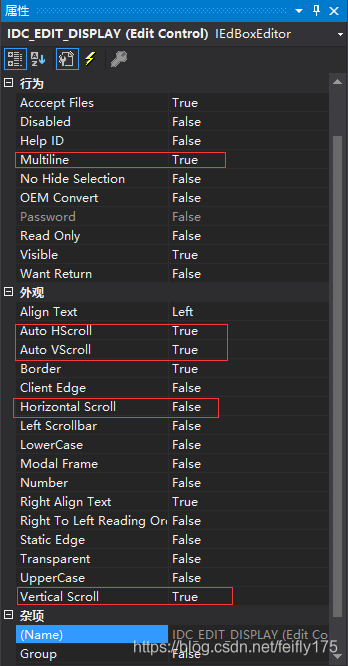

2.编辑框的内容的获取与显示

(1)使用GetDlgItemText( )和SetDlgItemText( )

void CSimpleCalculatorDlg::OnBnClickedButton1()
{
	CString cs;
	GetDlgItemText(IDC_EDIT_DISPLAY, cs);//获取编辑框中的内容
	SetDlgItemText(IDC_EDIT_DISPLAY, cs + _T("1"));//更新编辑框中的内容
}

(2)为编辑框添加CEdit类型变量edit

void CSimpleCalculatorDlg::OnBnClickedButton1()
{
	CString cs;
	edit.GetWindowTextW(cs); //获取编辑框内容
	cs = cs + _T("1");
	edit.SetWindowText(cs); //更新编辑框中的内容
}

(3)添加数值型的变量cstr

void CSimpleCalculatorDlg::OnBnClickedButton1()
{
	UpdateData(true);//获取编辑框中的内容到变量中
	cstr = cstr + _T("1");
	UpdateData(false);; //将变量中的值显示到编辑框内
}

五.代码实现

1.头文件部分

#include "pch.h"
#include "framework.h"
#include "Simple Calculator.h"
#include "Simple CalculatorDlg.h"
#include "afxdialogex.h"
#include "queue"
#include "stack"
using namespace std;

#ifdef _DEBUG
#define new DEBUG_NEW
#endif

2.全局变量

struct node {
	double number; //操作数
	char operat; //操作符
	bool flag; //操作数true、操作符false
};

CString hcs; //历史记录
CString re;    //表达式的结果
char str[100]; //存放中缀表达式的字符串
stack <node> opStack; //存放操作符的栈
queue <node> postQue; //存放后缀表达式

3.中缀表达式转成后缀表达式

void  CSimpleCalculatorDlg::Transition() { //中缀表达式转后缀表达式  
	node temp;
	for (int i = 0; i < strlen(str)-1;) { // 逐一扫描中缀表达式
		if (str[i] >= '0' && str[i] <= '9') {//如果是操作数，flag = false
			temp.flag = true; 
			temp.number = (double)str[i++]-'0'; //读取个位数字
			while (i <strlen(str)-1 && str[i] >= '0' && str[i] <= '9') {
				temp.number = temp.number * 10 + str[i++]-'0';
			} //判断是否有高位数字，并读取
			postQue.push(temp); //将操作数压入队列
		}
		else {
			temp.flag = false; // 如果是操作符，flag=false
			if (opStack.empty()) { //操作符栈为空，直接入栈
				temp.operat = str[i];
				opStack.push(temp);
			}
			else if (str[i] == '(') //遇到左括号直接入栈
			{
				temp.operat = str[i];
				opStack.push(temp);
			}
			else if (str[i] == ')') { //遇到右括号
				while (opStack.top().operat != '(') {
					postQue.push(opStack.top());
					opStack.pop();
				}
				opStack.pop();
			}
			else {
				while (!opStack.empty() && Priority(str[i]) <= Priority(opStack.top().operat)) {
					postQue.push(opStack.top());
					opStack.pop();
				} //若当前操作符优先级小于等于栈顶操作符，则将栈顶操作符压入队列中
				temp.operat = str[i];
				opStack.push(temp);
			}
			i++;
		}
	}
	while (!opStack.empty()) { //所有操作数入队列后，将栈中剩余操作符压入队列
		postQue.push(opStack.top());
		opStack.pop();
	}
}

4.计算后缀表达式

int  CSimpleCalculatorDlg::Priority(char op)  //定义运算符优先级 
{
	switch (op)
	{
	case'(':
		return 0;
	case '+':
	case '-':
		return 1;
	case '*':
	case '/':
		return 2;
	}
}
void CSimpleCalculatorDlg::Calculator() {
	double temp1, temp2;
	node curr, temp;
	while (!postQue.empty()) {
		curr = postQue.front(); //记录队列首元素
		postQue.pop();
		if (curr.flag == true) opStack.push(curr); //如果是操作数，压入栈中
		else { //如果是操作符
			temp2 = opStack.top().number; //先弹出第二个操作数
			opStack.pop();
			temp1 = opStack.top().number; //后弹出第一个
			opStack.pop();
			temp.flag = true; // 临时的node表示操作数，使用node是为了计算后，将临时数值结果压入栈中
			if (curr.operat == '+') {
				temp.number = temp1 + temp2;
			}
			else if (curr.operat == '-') {
				temp.number = temp1 - temp2;
			}
			else if (curr.operat == '*') {
				temp.number = temp1 * temp2;
			}
			else if(temp2!=0){
				temp.number = temp1 / temp2;//定义加减乘除操作
			}
			opStack.push(temp); //将临时结果压入栈中
		}
	}
	double result = opStack.top().number; //返回栈中仅有的元素，即最终结果
	re.Format(_T("%lf"), result);
	opStack.pop();
}

5.按钮选择在编辑框中的显示

void CSimpleCalculatorDlg::OnBnClickedButton1()//数字0~9以及运算符的类似
{
	// TODO: 在此添加控件通知处理程序代码
	CString cs;
	GetDlgItemText(IDC_EDIT_DISPLAY, cs);//获取编辑框中的内容
	SetDlgItemText(IDC_EDIT_DISPLAY, cs + _T("1"));//更新编辑框中的内容
}
void CSimpleCalculatorDlg::OnBnClickedButtonBackspace()//后退
{
	// TODO: 在此添加控件通知处理程序代码
	CString cs;
	GetDlgItemText(IDC_EDIT_DISPLAY, cs);
	cs.Delete(cs.GetLength()-1);
	SetDlgItemText(IDC_EDIT_DISPLAY, cs);
}
void CSimpleCalculatorDlg::OnBnClickedButtonClear()//清零
{
	// TODO: 在此添加控件通知处理程序代码
	SetDlgItemText(IDC_EDIT_DISPLAY, _T(""));
	re = _T("");
//	for(int i=0;i<strlen(str);i++){
//		str[i] = 0;
//	}
}
void CSimpleCalculatorDlg::OnBnClickedButtonEqual()//算术表达式的结果显示及历史记录的保存
{
	// TODO: 在此添加控件通知处理程序代码
	CString cs;
	CString cs1;
	GetDlgItemText(IDC_EDIT_DISPLAY, cs);
	int i;
	for ( i = 0; i < cs.GetLength(); i++) {
		str[i] = cs[i];
	}
	str[i] = '/0';
	Transition();
	Calculator();
	SetDlgItemText(IDC_EDIT_DISPLAY, cs + _T("=") + re);
	GetDlgItemText(IDC_EDIT_DISPLAY, cs1);
//	if (hcs.IsEmpty()) {//最新的历史记录在底部
//		hcs = hcs + cs1;
//	}
//	else {
//		hcs = hcs + "\r\n" + cs1;
//	}
	hcs = cs1 + "\r\n" + hcs; //最新的历史记录在顶部
}
void CSimpleCalculatorDlg::OnBnClickedButtonHistory()
{
	// TODO: 在此添加控件通知处理程序代码
	//edit.SetWindowText(hcs);
	SetDlgItemText(IDC_EDIT_DISPLAY, hcs);
}

六.调试结果

1.表达式的计算（计算结果为double类型）

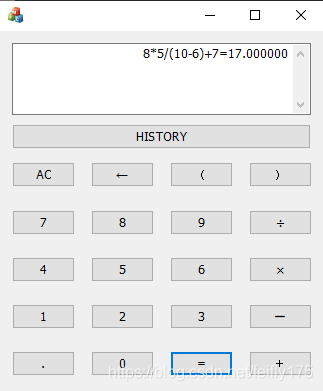
2历史记录的显示

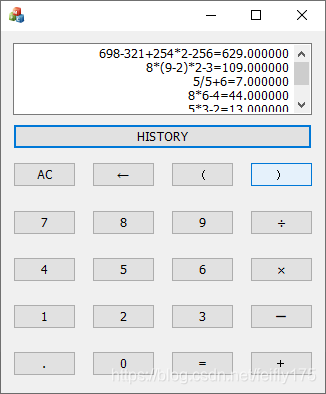
七.总结

以上只能实现整数的混合四则运算，小数运算以及三角函数的运算、对数运算、指数运算、进制转换等还有待进一步的完善。