异质信息网络中的节点排序算法 ObjectRank 和 PopRank

原文地址：https://dreamhomes.github.io/posts/202007261112.html

背景

现实中的复杂系统大体可以抽象为两类：第一类是同质信息网络(Homogeneous
information network)，这种建模方法仅抽取网络中部分信息并且没有区分对象或者关系间的差异性；第二类是异质信息网络(Heterogeneous information network)，网络中包含多种类型的关系和对象，具有全面的结构信息和丰富的语义信息。

目前同质信息网络中节点排序方法较多且应用较广，例如Personalized PageRank ，其计算公式如下所示：
$${\mathbf{P}\mathbf{P}\mathbf{R}}_q=(1-\alpha )M^T\times {\mathbf{P}\mathbf{P}\mathbf{R}}_q+\alpha \mathbf{q}$$

但是其不适用于异质信息网络。因此介绍当前的两种适用于异质信息网络中节点排序的方法 ObjectRank和PopRank，主要思想借鉴PageRank。

ObjectRank

ObjectRank 主要用于数据库中查询内容，根据输入的关键字对内容进行排序输出。

以 DBLP 数据库说明下术语及其含义，并给出算法过程。

• Label / Data Graph
  
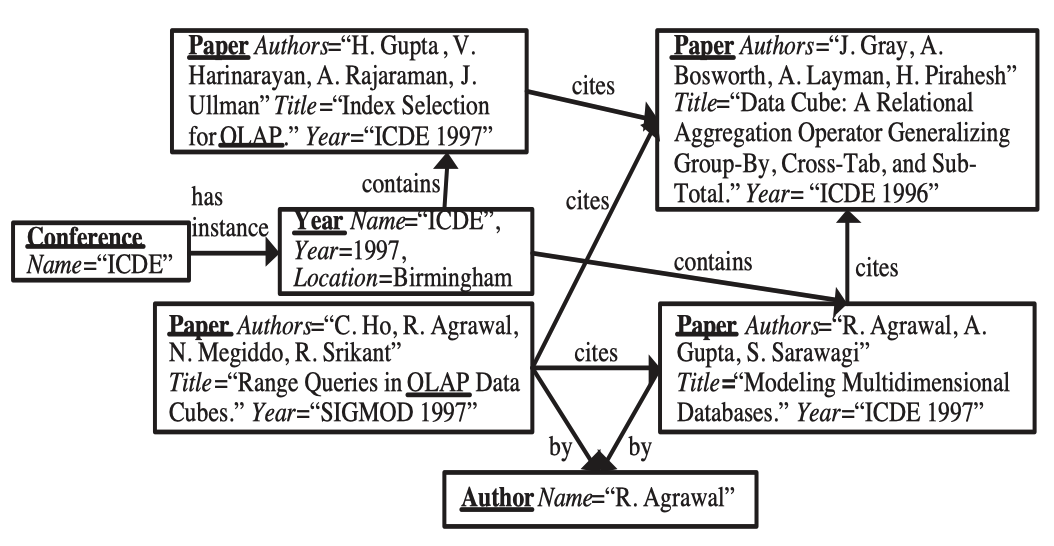
• Schema Graph
  
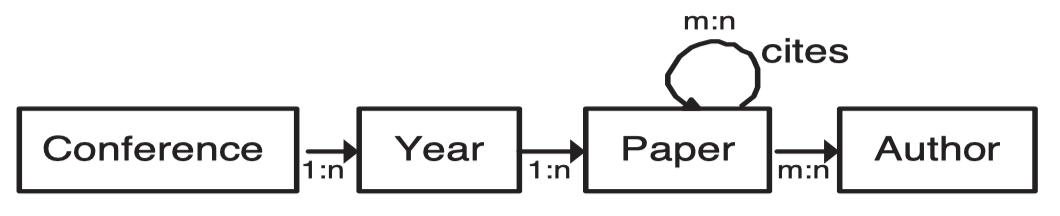
• Authority transfer schema graph
  
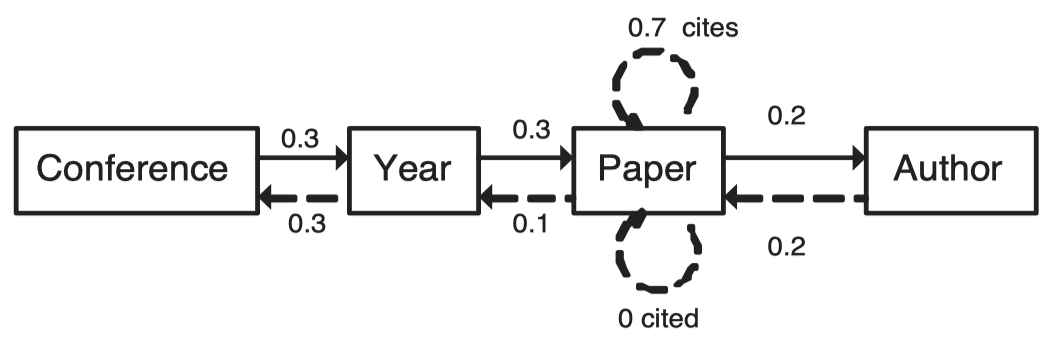
• Authority Transfer Data Graph
  
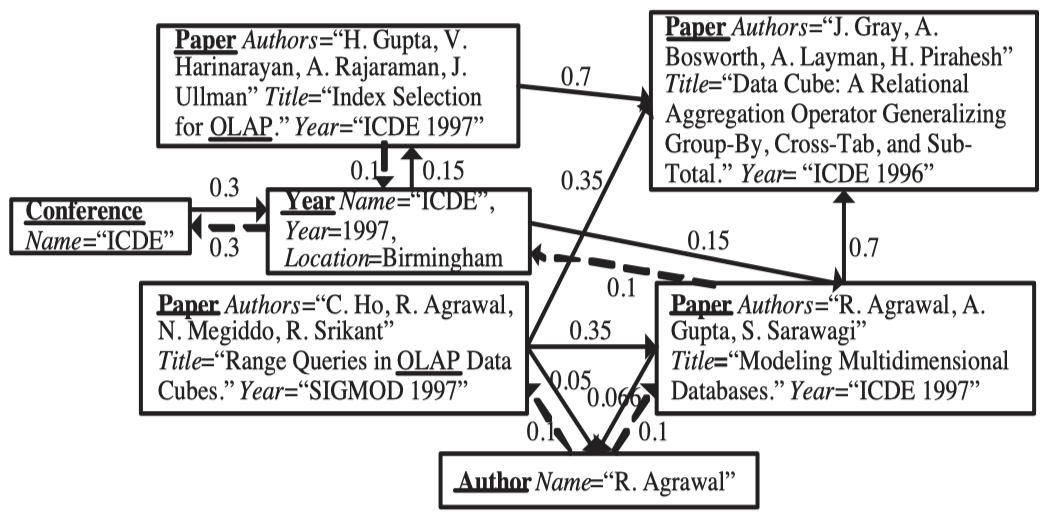
• 对于关键字 “OLAP” 的查询结果
  

算法过程

以给定的模式图（Schema Graph） $G(V_G,E_G)$ 来建模复杂系统，每个对象包含多个属性-值对。根据模式图需要定义一个权威概率转移模式图（authority transfer schema graph）$G^A(V_G,E_G^A)$，图中每条边的转移概率是依据专家知识定义的。给定数据图（data graph）$D(V_D,E_d)$可以根据$G(V_G,E_G)$和$G^A(V_G,E_G^A)$可以得到一个权威性转移数据图$D^A(V_D,E_D^A)$。

对于图中任意两个对象 $u$ 和 $v$间的转移概率可以定义为：
$$M(u,v)=\{\begin{array}{ll}\frac{w(T)}{d_{out}(u,T)}& \text{ if }{d}_{out}(u,T)>0\\ 0& \text{ if }{d}_{out}(u,T)=0\end{array}$$
式中 $T$表示边$(u,v)$的类型，$w(T)$表示边类型为$T$的权威转移概率，$d_{out}(u,T)$表示节点$u$所有出边类型为 $T$ 的边数量。

在定义权威性转移数据图并得到节点带你转移概率矩阵 $M$ 之后，其在线查询过程与Personalized PageRank 类似。

对于一个查询关键字 $k$ ，系统将会根据包含该关键字的对象准备一个查询向量 $\mathbf{q}$，如果一个对象 $u$ 包含关键字 $k$，那么 $q(u)=1/N_k$，否则$q(u)=0$， 其中$N_k$表示所有包含该关键字的对象数量。那么对于给定的关键字 $k$其 ObjectRank vector为：
$${\mathrm{O}\mathrm{R}}_q=(1-\alpha )M^T\times {\mathrm{O}\mathrm{R}}_q+\alpha \mathrm{q}$$
其中$\alpha$阻尼参数。

PopRank

PopRank主要用于网页排序，考虑了网页流行度和其它类型对象的影响，计算公式如下：
$${\mathbf{R}}_X=ϵ{\mathbf{R}}_{EX}+(1-ϵ)\sum _Y{\gamma }_{YX}{M}_{YX}^T{\mathbf{R}}_Y$$
其中 $ϵ$ 为加权参数，${\gamma }_{YX}$ 表示从类型为$Y$的对象到类型为$X$的对象的流行度传播因子(PPF)，${\sum }_Y{\gamma }_{YX}=1$；$M_{YX}$是类型$Y$和类型$X$间的邻接矩阵；$R_Y$ 是类型 Y 的PopRank vector。

论文中还提出了模拟退火算法来学习流行传播因子 ${\gamma }_{YX}$，想了解可以阅读原论文。Object-Level Ranking: Bringing Order to Web Objects