Volume of n-simplex | n维单纯形的体积

An is an n-simplex which is supported by n vectors (a1,a2,…,an) of same origin.
Vn is the signed volume of An.

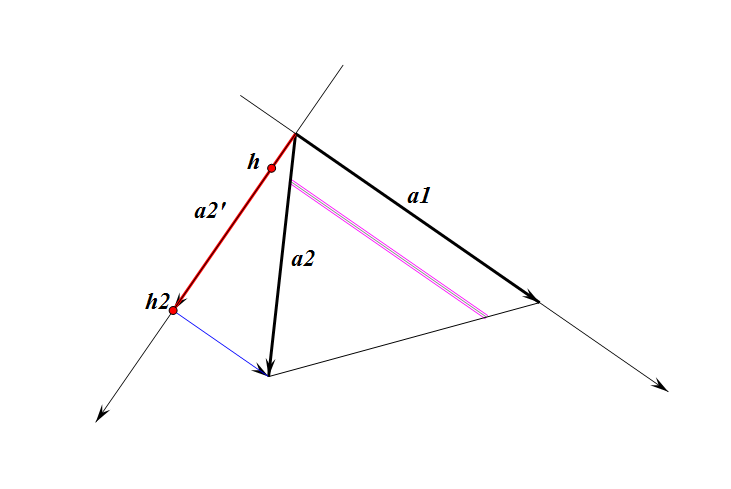
After we apply Gram–Schmidt orthogonalization to (a1,a2,…,an), we will get (a1,a2’,…,an’), the orthogonal basis of n-dimensional vector space.
Transpose of a1 =(h1,0,…,0)
Transpose of a2’=(0,h2,…,0)
…
Transpose of an’=(0,0,…,hn)

① V1=h1
② t = h2-h

$$V_{2}=\int_{0}^{h_{2}} V_{1}\left ( \frac{t}{h_{2}} \right )\,{\rm d}t$$
$$V_{3}=\int_{0}^{h_{3}}V_{2}\left ( \frac{t}{h_{3}} \right )^{2}\,{\rm d}t$$
$$...$$
$$V_{n}=\int_{0}^{h_{n}}V_{n-1}\left ( \frac{t}{h_{n}} \right )^{n-1}\,{\rm d}t$$
$h_n\,,V_{n-1}$can be + or -.
$t/h_n$should always be (and it will be) + to make $V_{n-1}$and $V_{n-1}\left ( \frac{t}{h_{n}} \right )^{n-1}$the same sign.

$$V_{n}=\frac{V_{n-1}}{h^{n-1}_{n}}\left. \frac{t^{n}}{n}\right|_{0}^{h_{n}}=\frac{h_{n}}{n}V_{n-1}=\frac{h_{n}}{n}\frac{h_{n-1}}{n-1}V_{n-2}=...=\frac{h_{n}h_{n-1}...h_{2}}{n!}V_{1}=\frac{1}{n!}h_{n}h_{n-1}...h_{1}$$
$$=\frac{1}{n!}det(a1,a2',...,an')=\frac{1}{n!}det(a1,a2,...,an)$$

$a_{2}'=a_{2}-c_{21}·a_{1}$
$a_{3}'=a_{3}-c_{31}·a_{1}-c_{32}·a_{2}$
$a_{4}'=a_{4}-c_{41}·a_{1}-c_{42}·a_{2}-c_{43}·a_{3}$
…
$a_n'=a_n-c_{n1}·a_1-c_{n2}·a_2-...-c_{nn-1}·a_{n-1}$

$\phantom{=}\: det(a1,a2',...,an')$
$=det(a1,a2,a3',...,an')$
$=det(a1,a2,a3,...,an')=...$
$=det(a1,a2,...,a_{n-1},an')$
$=det(a1,a2,...,an)$

Reference
- Simplex Volumes and … http://mathpages.com/home/kmath664/kmath664.htm
- Volume of n-d parallelepiped http://blog.csdn.net/u010476094/article/details/44746143