BST树（二叉排序树或二叉搜索树）的插入操作

构造一颗二叉排序树如下：

 代码如下：

#include <stack>
#include <queue>
using namespace std;
template<typename T, typename Comp = less<T>>
class BSTree
{
public:
	BSTree() :root_(nullptr) {}
	~BSTree() {}

	//非递归插入操作
	void n_insert(const T& val)
	{   //树为空，生成根节点
		if (root_ == nullptr)
		{
			root_ = new Node(val);
			return;
		}

		//搜索合适的插入位置，记录父节点的位置
		Node* parent = nullptr;
		Node* cur = root_;
		while (cur != nullptr)
		{
			if (cur->data_ == val)
			{
				//不插入元素相同的值
				return;
			}
			else if (comp_(cur->data_, val))
			{
				parent = cur;
				cur = cur->right_;
			}
			else
			{
				parent = cur;
				cur = cur->left_;
			}
		}
		//新节点插入到parent节点的孩子上
		if (comp_(val, parent->data_)) // val < parent->data_
		{
			parent->left_ = new Node(val);
		}
		else
		{
			parent->right_ = new Node(val);
		}
	}

	private:

		struct Node
		{
			Node(T data = T())
				:data_(data)
				, left_(nullptr)
				, right_(nullptr)
			{}
			T data_;//数据域
			Node* left_;//左孩子域
			Node* right_;//右孩子域
		};
	Node* root_;//指向BST树的根节点
	Comp comp_; //定义一个函数对象
};


int  main()

{
	int ar[] = { 58,24,67,0,34,62,69,5,41,64,78 };
	BSTree<int>bst;
	for (int v : ar)
	{
		bst.n_insert(v);
	}
	bst.n_insert(12);
	return 0;
}

调试结果如下：

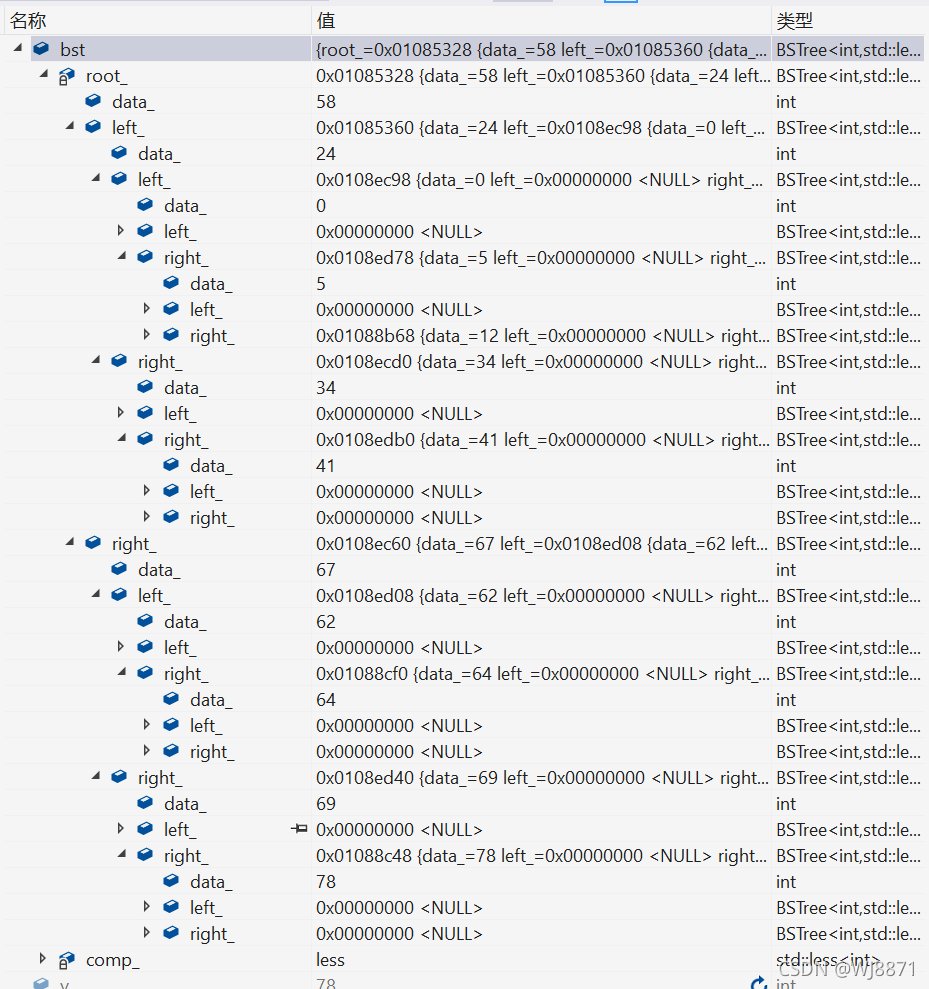
 插入节点12，12应为5的右孩子，思路为：

12小于58，此时parent指向58，cur指向58的左孩子24；

继续判断：12小于24，parent指向24，cur指向24的左孩子0；

继续判断：12大于0，parent指向0，cur指向0的右孩子5；

继续判断：12大于5，parent指向5，cur应指向5的右孩子（此时还没有创立节点）；

此时创建新节点，赋其数据为12，并让5的右孩子指向该节点。

可看到插入成功：