2.3分治算法

将原问题分解为几个规模较小但类似于原问题的子问题，递归的求解这些子问题，然后再合并这些子问题的解来建立原问题的解。
分解—解决—合并
$\theta$=(n$lg$n)

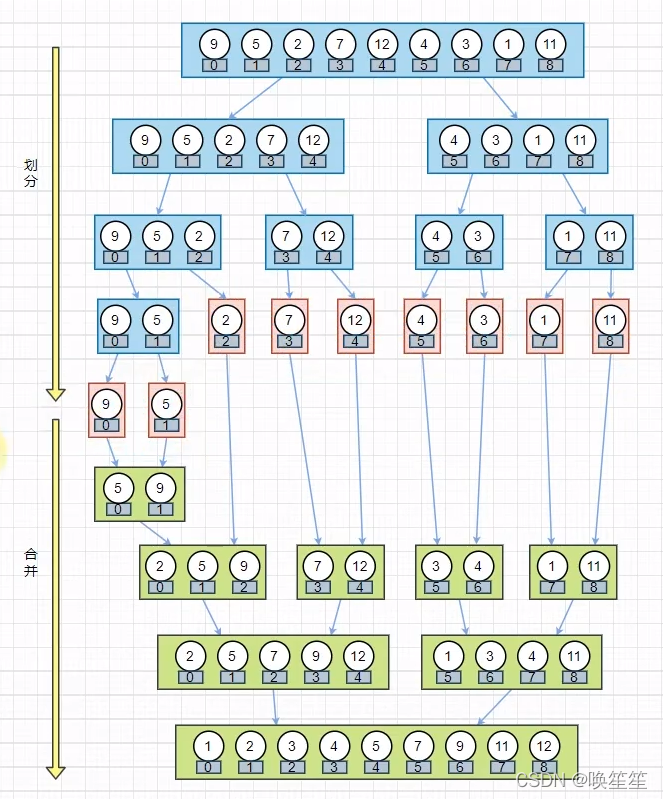
按照书中的方式编写的代码，采用两个函数递归调用：

# merge(合并)函数在改写A
def merge(A, p, q, r):
    n_1 = q - p + 1
    n_2 = r - q
    L = [0] * (n_1 + 1)
    R = [0] * (n_2 + 1)
    for i in range(0, n_1):
        L[i] = A[p + i]
    for j in range(0, n_2):
        R[j] = A[q + 1 + j]
    L[n_1] = float('inf')
    R[n_2] = float('inf')
    i = 0
    j = 0
    for k in range(p, r + 1):
        if L[i] < R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1


# 分函数
def merge_sort(A, p, r):
    if p < r:
        q = (p + r) // 2
        merge_sort(A, p, q)
        merge_sort(A, q + 1, r)
        merge(A, p, q, r)
    return A


print(merge_sort([5, 2, 4, 7, 1, 3, 2, 6], 0, 7))

代码如下（示例）：采用一个函数的方法

# 从lft和rgt的头部开始取较小的元素，进行升序排列
class Solution(object):
    def merge(self, A):
        mid = len(A) // 2
        lft = A[:mid]
        rgt = A[mid:]

        # 递归分治
        if len(lft) > 1:
            lft = self.merge(lft)
        if len(rgt) > 1:
            rgt = self.merge(rgt)
        # 合并
        res = []
        while lft and rgt:  # 遍历取出lft和rgt头部较小的元素储存在res中
            if lft[0] > rgt[0]:
                res.append(rgt.pop(0))#将rgt替换为lft,以及else中的lft替换为rgt，变成降序排列
            else:
                res.append(lft.pop(0))
        return res + (lft or rgt)


a = Solution()
print(a.merge([5, 2, 4, 7, 1, 3, 2, 6]))

#从rgt和lft的尾部开始取较大的元素，进行升序排列
class Solution(object):
    def merge_sort(self,nums=list):
        # 取mid以及左右两个数组
        mid = len(nums) // 2
        left_nums, right_nums = nums[:mid], nums[mid:]

        # 递归分治
        if len(left_nums) > 1:
            left_nums =self. merge_sort(left_nums)
        if len(right_nums) > 1:
            right_nums = self.merge_sort(right_nums)

        # 合并
        res = []
        while left_nums and right_nums:  # 遍历取出lft和rgt尾部较大的元素储存在res中
            if left_nums[-1] >= right_nums[-1]:  # 尾部较大者
                res.append(left_nums.pop())#将lft替换为rgt,以及else中的rgt替换为lft，变成降序排列
            else:
                res.append(right_nums.pop())
        res.reverse()  # 倒序
        return (left_nums or right_nums) + res  

a = Solution()
print(a.merge_sort([5, 2, 4, 7, 1, 3, 2, 6]))

习题2.3-2

代码如下（示例）：

# merge(合并)函数在改写A
def merge(A, p, q, r):
    n_1 = q - p + 1
    n_2 = r - q
    L = [0] * (n_1)
    R = [0] * (n_2)
    for i in range(0, n_1):
        L[i] = A[p + i]
    for j in range(0, n_2):
        R[j] = A[q + 1 + j]
    i = 0
    j = 0
    k = p
    while i < n_1 and j < n_2:
        if L[i] < R[j]:
            A[k] = L[i]
            i += 1
        else:
            A[k] = R[j]
            j += 1
        k += 1
    while i < n_1:
        A[k] = L[i]
        i += 1
        k += 1
    while j < n_2:
        A[k] = R[j]
        j += 1
        k += 1


# merge_sort分函数
def merge_sort(A, p, r):
    if p < r:
        q = (p + r) // 2
        merge_sort(A, p, q)
        merge_sort(A, q + 1, r)
        merge(A, p, q, r)
    return A


print(merge_sort([3, 41, 52, 26, 38, 57, 9, 49], 0, 7))

习题2.3-3

当$n=2$时：$T(2)=2lg2$
当$n=2^t$时：$T(2^t)=(2^t)\ast lg(2^t)$
当$n=2^{t+1}$时：
$$\begin{gathered} T(2^{t+1})=2\ast T(\frac{2^{t+1}}{2})+2^{t+1} \\ =2\ast T(2^t)+2^{t+1} \\ =2\ast (2^t)\ast lg(2^t)+2^{t+1} \\ =2^{t+1}\ast lg(2^t)+2^{t+1}=2^{t+1}\ast (lg(2^t)+1)=2^{t+1}\ast (lg{2}^{t+1}) \end{gathered}$$
故而$T(n)=nlg(n)$

习题2.3-4

$T(n)=\{\begin{array}{rl}1& \text{if }n<0,\\ T(n-1)+\Theta (n)& \text{if }n>1,\end{array}$
最糟糕情况：当n=1时，往前查找一次即可；当n>1需要往前查找判断n次

习题2.3-5

# 二分查找
class Solution(object):
    def generate(self, A, b):
        A.sort()
        low = 0
        high = len(A) - 1
        while low <= high:
            mid = (low + high) // 2
            if b == A[mid]:
                return mid
            elif b < A[mid]:
                high = mid - 1
            else:
                low = high + 1
        return None


a = Solution()
print(a.generate([1, 2, 3, 4, 5, 6], 1))

习题2.3-6

在最坏情况下，二分查找的时间复杂度时$\Theta (nlgn)$,但插入数组移动的时间复杂度仍然是$n^2$。故而总体运行时间不能得到改善。

习题2.3-7

# 因为复杂度中有lgn,故而要采用二分查找
class Solution(object):
    def checksum(self, A, b):
        A.sort()
        n = len(A)
        for i in range(n):#for循环迭代元素
            low = i + 1
            high = n - 1
            while low <= high:
                mid = (high - low) // 2 + low
                if A[mid] == b - A[i]:
                    return True
                if A[mid] > b - A[i]:
                    high = mid - 1
                if A[mid] < b - A[i]:
                    low = mid + 1
        return False


a = Solution()
print(a.checksum([5, 2, 4, 6, 1, 3], 12))

# 采用两个for循环，类似于双指针
class Solution(object):
    def checksum(self, A, b):
        A.sort()
        n = len(A)
        for i in range(n - 1):
            for j in range(i + 1, n):
                if b == A[i] + A[j]:
                    return True

        return False
a = Solution()
print(a.checksum([5, 2, 4, 6, 1, 3], 1))

思考题2-4(d)用二分法计算逆序对

def merge(A, p, q, r):
    n_1 = q - p + 1
    n_2 = r - q
    L = [0] * (n_1 + 1)
    R = [0] * (n_2 + 1)
    for i in range(0, n_1):
        L[i] = A[p + i]
    for j in range(0, n_2):
        R[j] = A[q + 1 + j]
    L[n_1] = float('inf')
    R[n_2] = float('inf')
    i = 0
    j = 0
    inversion=0
    counted=False
    for k in range(p, r + 1):
        if counted==False and R[j]<L[i]:
            inversion=inversion-i+n_1
            counted=True
        if L[i] <= R[j]:
            A[k] = L[i]
            i += 1
        else:  # 触发此步表明有逆序对
            A[k] = R[j]
            j += 1
            counted=False

    return inversion


# 分函数
def merge_sort(A, p, r):
    inversions = 0
    if p < r:
        q = (p + r) // 2
        inversions = inversions + merge_sort(A, p, q)
        inversions = inversions + merge_sort(A, q + 1, r)
        inversions = inversions + merge(A, p, q, r)

    return inversions


print(merge_sort([2,3,8,6,1], 0, 4))

class Solution(object):
    def reversePairs(self, A):
        nums = 0

        def merge(A, nums):
            mid = len(A) // 2
            lft = A[:mid]
            rgt = A[mid:]
            # 递归分治
            if len(lft) > 1:
                lft, nums = merge(lft, nums)
            if len(rgt) > 1:
                rgt, nums = merge(rgt, nums)
            # 合并
            res = []
            while lft and rgt:  # 遍历取出lft和rgt头部较小的元素储存在res中
                if lft[0] > rgt[0]:
                    res.append(rgt.pop(0))  # 将rgt替换为lft,以及else中的lft替换为rgt，变成降序排列
                    nums += len(lft)
                else:
                    res.append(lft.pop(0))
            return res + (lft or rgt), nums

        new_A, nums = merge(A, nums)
        return nums


a = Solution()
print(a.reversePairs([7, 5, 6, 4]))