目录
一.插入排序
1.插入排序思想
就是将待排序的数字插入到已经排序好的指定位置即可，直到所有需要排序的数字都插入到序列即可，从而得到一个有序的序列。（相当于我们平常玩扑克牌时将接到的牌插入到指定的位置）
2.动态图形演示
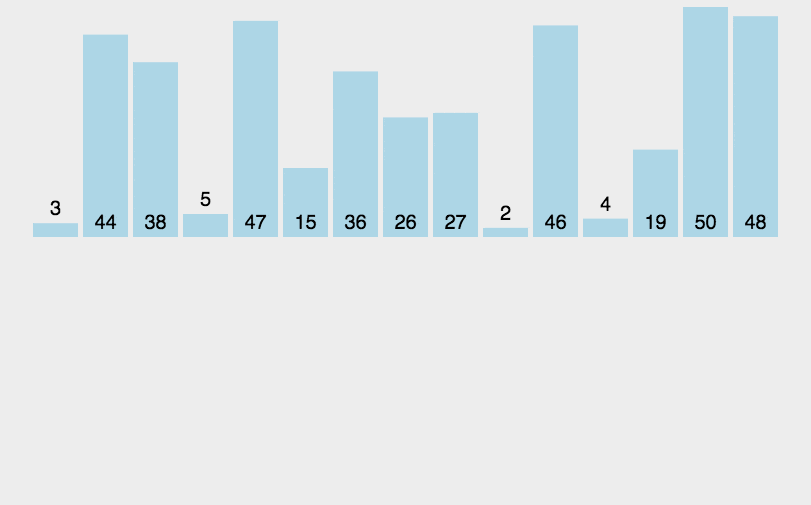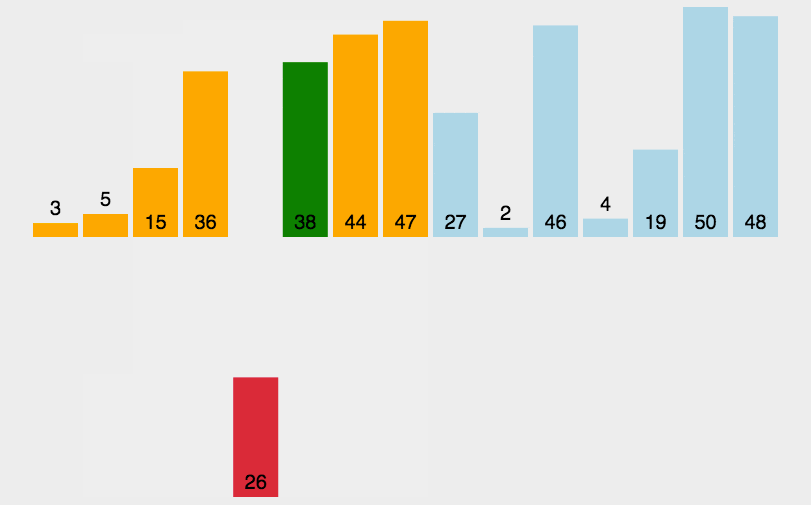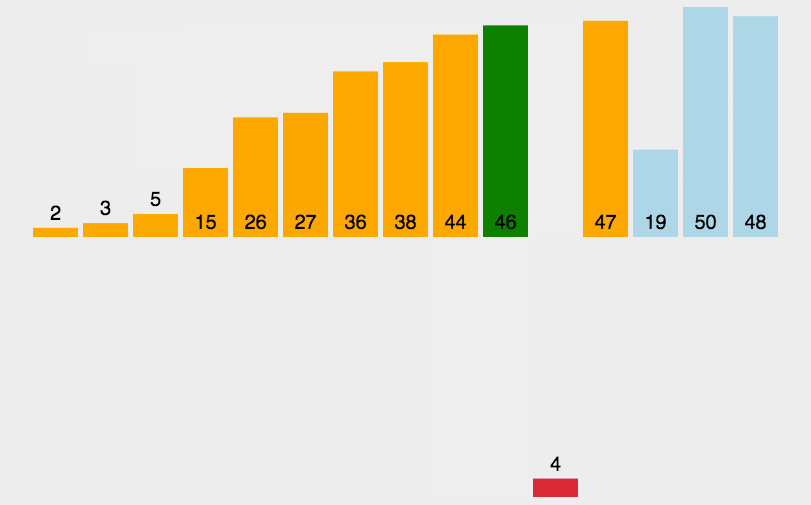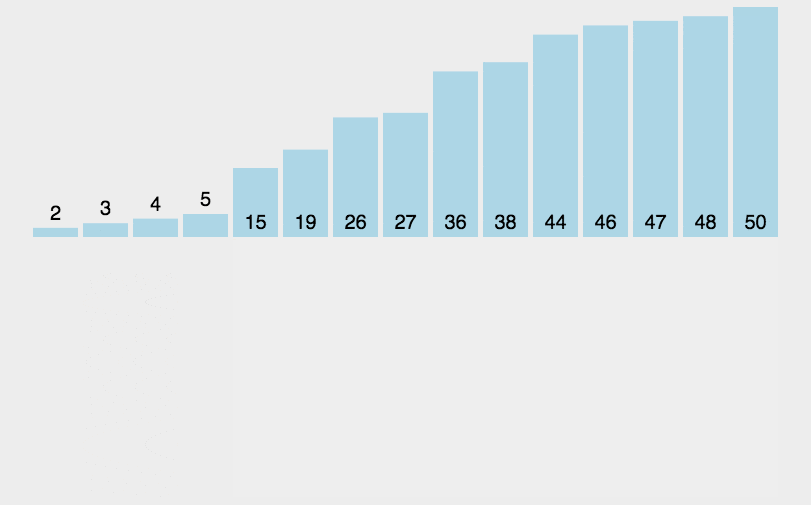
3.插排思路与图解
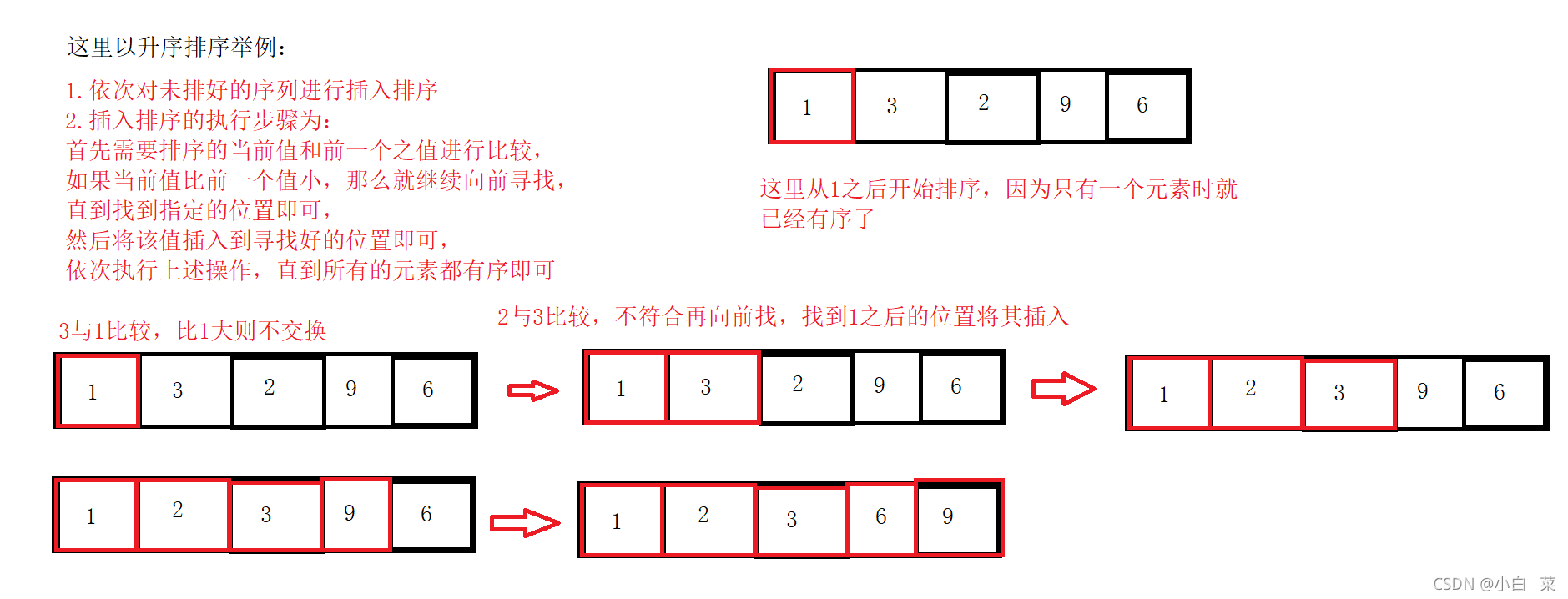
4.插入排序代码实现（升序）
（1）控制排序的次数，保存需要插入的值。
（2）将大的元素向后移，找到合适的位置。
（3）将元素插入指定位置，然后继续执行上述操作。
（4）这里需要注意在找的时候可能会到最前面，需要注意数组越界问题。
代码实现：
//插入排序(升序)
public static void insertSort(int[] arr){
//排序的次数
for(int i=1;i<arr.length;i++){
int end=arr[i];//保存需要插入的值
int k=i-1;//保存需要插入的位置
while(k>=0 && arr[k]>end){//寻找需要插入的位置
arr[k+1]=arr[k];
k--;
}
arr[k+1]=end;//将元素是插入到指定的位置
}
}5.时间复杂度，空间复杂度及稳定性
（1）时间复杂度：O(N^2)
（2）空间复杂度：O(1)
执行过程中没有借助辅助空间。
（3）什么是稳定性
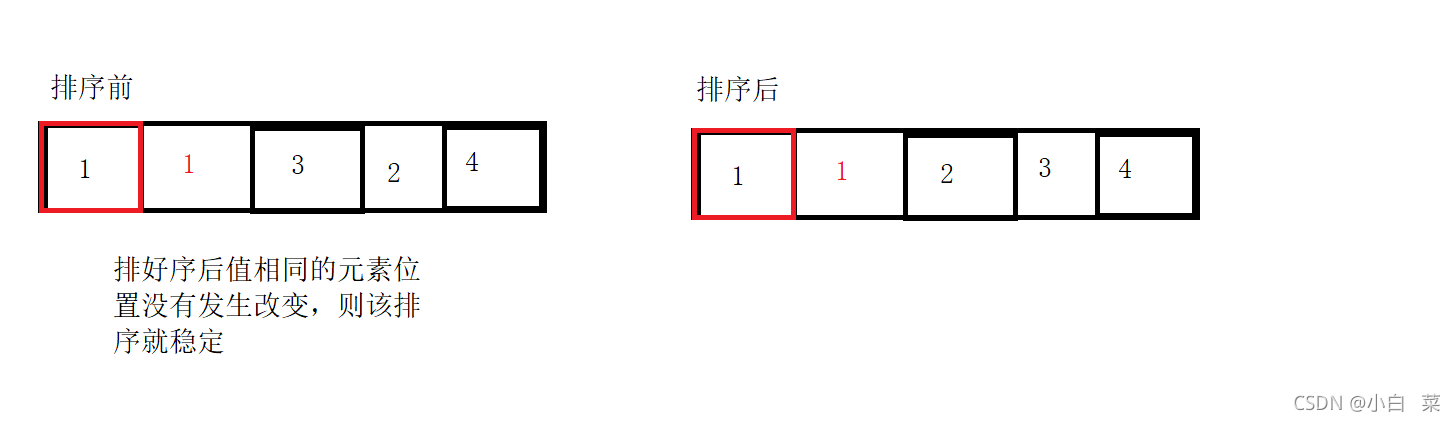
（4）稳定性：稳定
6.应用场景
适合于基本有序的数组或者数据量特别小的数组，因为基本有序，那么中间进行比较的次数就会减少。
二.希尔排序
1.引言
如果需要排序的数字量特别多而且比较凌乱，而且还需要使用插入排序，这时候就有了希尔排序。
2.希尔排序思想
先选定一个合适的距离，然后以该距离为分割长度，依次对该距离的所有元素进行插入排序，然后再缩小这个距离，直到距离为1时结束。
3.希尔排序动图
4.希尔排序思路图解
这里每次对于gap间距的值为gap=gap/3+1来处理
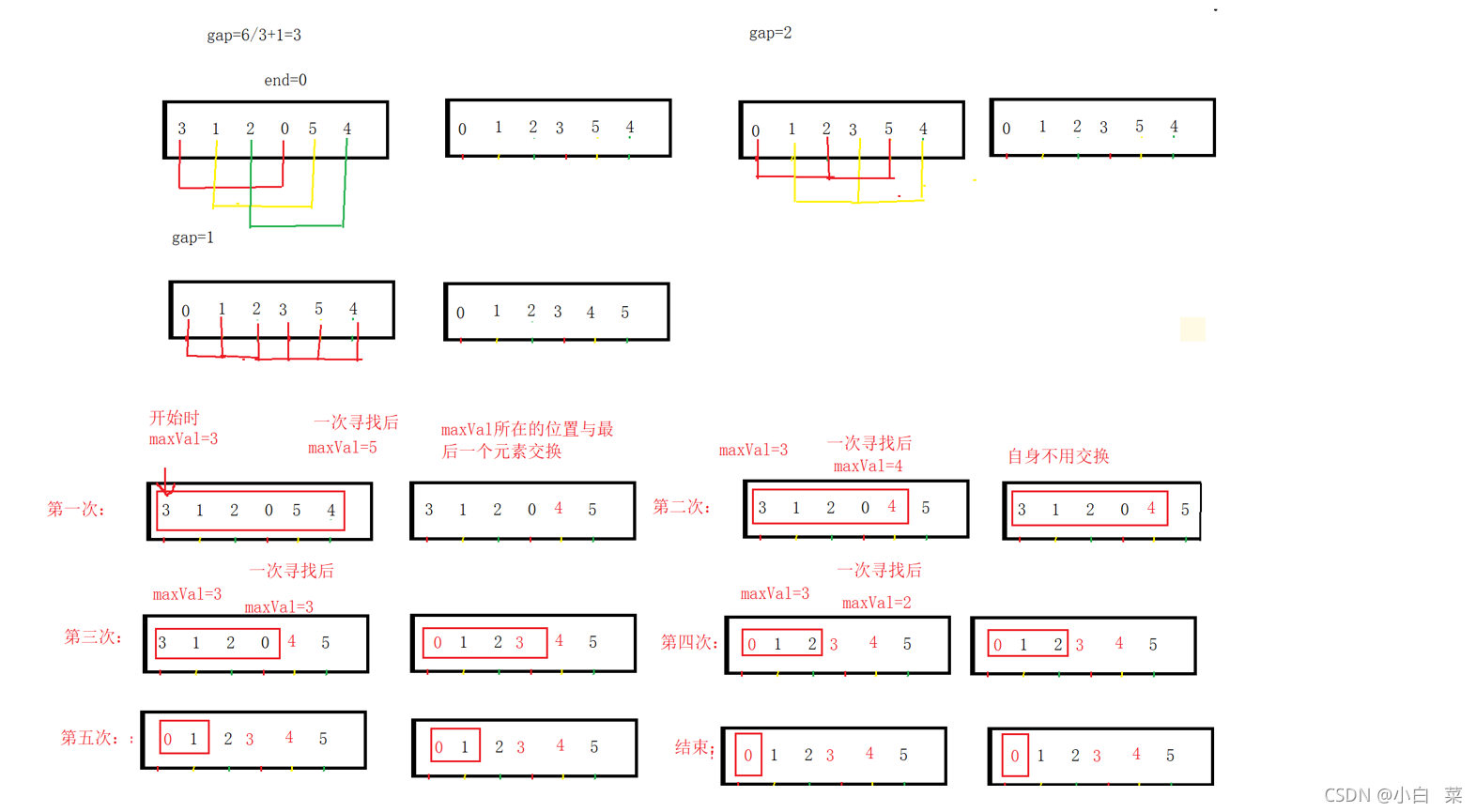5.代码实现
public static void shellSort(int[] arr){
int gap=arr.length;
while(gap>1){
gap= gap/3+1;
for(int i=gap;i<arr.length;i++){
int end=arr[i];
int k=i-gap;
while(k>=0 && arr[k]>end){
arr[k+gap]=arr[k];
k-=gap;
}
arr[k+gap]=end;
}
}
}6.时间复杂度，空间复杂度及稳定性分析
（1）时间复杂度
如果gap选取的不同，则时间复杂度就，对于希尔排序，时间复杂度没有一个确定的值，当前增量法的时间复杂度大致为O(N^1.25)到O(1.6N^1.25)之间。
（2）空间复杂度
O(1)
（3）稳定性分析
由于每次都时间隔排序，所以不稳定
7.应用场景
对于数据量特别大，数字比较凌乱的情况下，而且还需要使用插入排序的情况下,可以使用希尔排序来进行处理。
三.选择排序（升序）
1.排序思想
每次选择一个最大的数放在数组的末尾（或者每次选择一个最下的放在数组头，起始位置后移），然后数组长度-1，接着使用该方法，直到所有的元素排序完成即可。
2.选择排序动态图示
3.思路图解
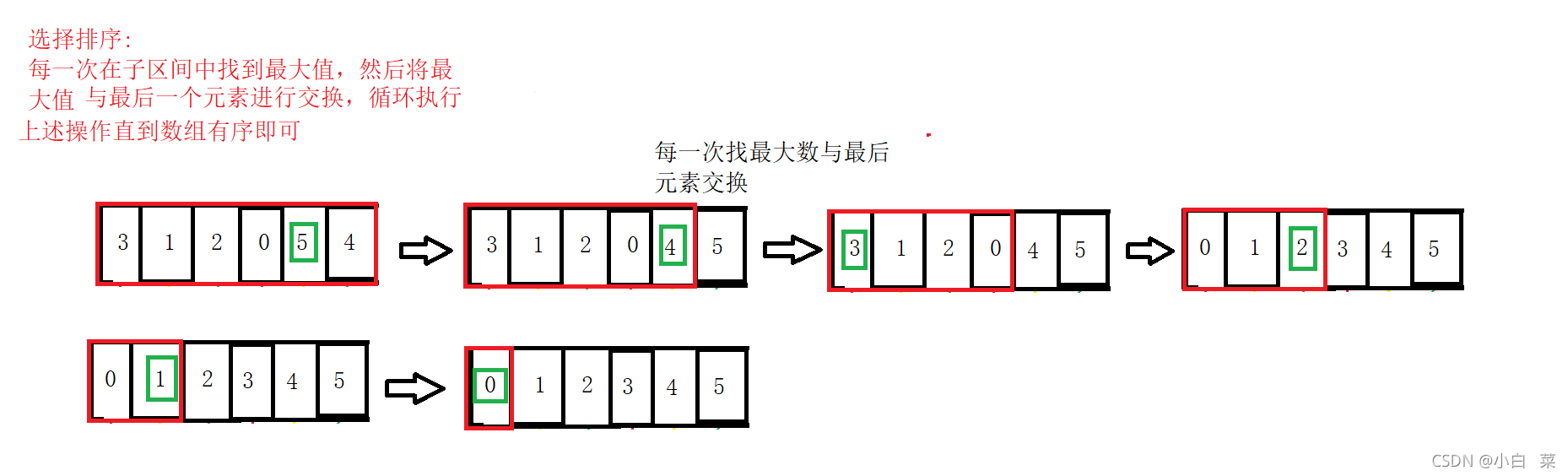
4.代码实现
//选择排序（每次选最大的元素放在数组末尾）
public static void selectSort(int[] arr){
for(int i=0;i<arr.length-1;i++){
int maxVal=0;
for(int j=1;j<arr.length-i;j++){
if(arr[maxVal]<arr[j]){
maxVal=j;
}
}
if(maxVal!=arr.length-i)
swap(arr,maxVal,arr.length-1-i);
}
}
public static void swap(int[] arr,int left,int right){
int tmp=arr[left];
arr[left]=arr[right];
arr[right]=tmp;
}5.时间复杂度，空间复杂度及稳定性分析
（1）时间复杂度
每一个元素都与前n-i-1个元素进行比较，所以时间复杂度为O(N^2)
（2）空间复杂度
没有额外空间的开辟，所以空间复杂度为O(1)
（3）稳定性
由于每次都是间隔进行交换，所以相同的元素最后位置可能会改变，所以不稳定。
6.应用场景
由于时间复杂度不好，平时应用的比较少。
四.堆排序
1.堆排序的排序思想
堆排序)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。
2.堆排序动图演示
3.思路图解及代码实现
深入了解点击下面链接：
（1）思路分析（升序为例）
首先需要创建一个堆，然后再根据当前堆来模拟删除（这里的删除思路是堆顶元素与当前数组的最后一个元素进行交换（这时候最后一个元素就是当前的最大值，这时候可能就不满足大顶堆了，就需要重新进行向下调整了））。
向下调整（大顶堆为例）的思想是先找出以当前为parent节点，然后找出左右（如果存在右孩子），找出最大的孩子节点与父节点进行比较，如果不满足堆性质，就一直进行向下调整。
（2）代码实现
//堆排序
public int[] heapSort(int[] nums) {
//建堆
int size = nums.length;
//最后一个节点减一，由于数组长度不是最后一个元素索引位置，所以减二
int lastLeaf = (size-2)/2;
for(int root = lastLeaf; root>=0; root--) {
shiftDown(nums, size, root);
}
//排序操作（相当于删除）
int end = size-1;
while(end>0) {
swap(nums, 0, end);
shiftDown(nums, end, 0);
end--;
}
return nums;
}
public void shiftDown(int[] nums, int size, int parent) {
int child = parent*2+1;
while(child<size) {
//找出左右孩子的最大值
if(child+1<size && nums[child]<nums[child+1]) {
child+=1;
}
//判断最大孩子与父节点的值是否满足堆性质，不满足继续向下调整
if(nums[parent]<nums[child]) {
swap(nums, parent, child);
parent = child;
child = parent*2+1;
}else {
//满足堆性质,结束
return;
}
}
}
public void swap(int[] nums, int left, int right) {
int tmp = nums[left];
nums[left] = nums[right];
nums[right] = tmp;
}4.时间复杂度，空间复杂度及稳定性
（1）时间复杂度
因为堆排序相当于删除元素，所以删除需要N次，然后每次向下调整最坏为二叉树的层数为
,
所以时间复杂度为O(N*)
（2）空间复杂度
O(1)
（3）稳定性
由于间隔进行交换，所以不稳定。
5.应用场景
需要前k个最大或最小元素时，或者与其他排序一块使用
五.冒泡排序
1.排序思想
大的元素向下沉，小的元素向上浮。
2.冒泡排序动图演示
3.冒泡排序图解
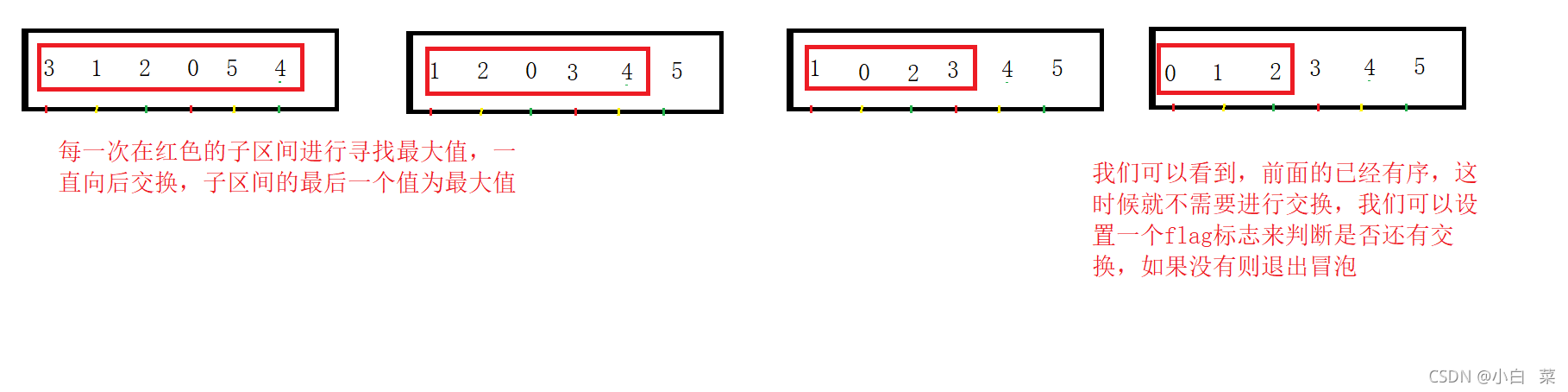
4.冒泡排序代码：
//冒泡排序
public static void bubbleSort(int[] arr){
//冒泡的趟数
for(int i=0;i<arr.length-1;i++){
boolean flag = false;//判断是否交换
//在子区间进行冒泡
for(int j=0;j<arr.length-1-i;j++){
if(arr[j]>arr[j+1]){
swap(arr,j,j+1);//交换2个元素
flag=true;
}
}
//没有再进行交换则退出
if(!flag){
return;
}
}
}
public static void swap(int[] arr,int left,int right){
int tmp=arr[left];
arr[left]=arr[right];
arr[right]=tmp;
}5.时间复杂度，空间复杂度及稳定性
（1）时间复杂度
O(N^2)
（2）空间复杂度
O(1)
（3）稳定性
没有间隔进行交换，所以稳定
6.应用场景
基本不使用
六.快速排序
1.快速排序思想
任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
原理：以基准值为中心，将区间划分为左边的值都小于基准值，右边的值都大于基准值，直到所有元素有序即可。
2.快速排序动图演示
3.思路图解
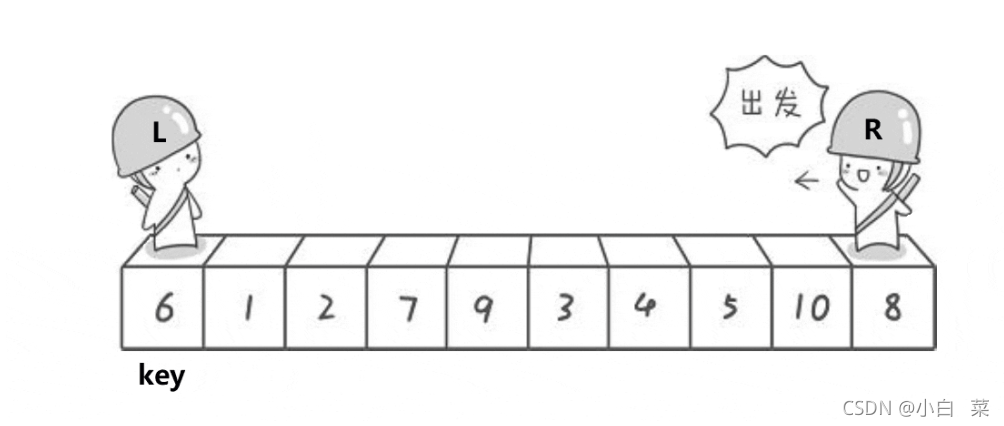
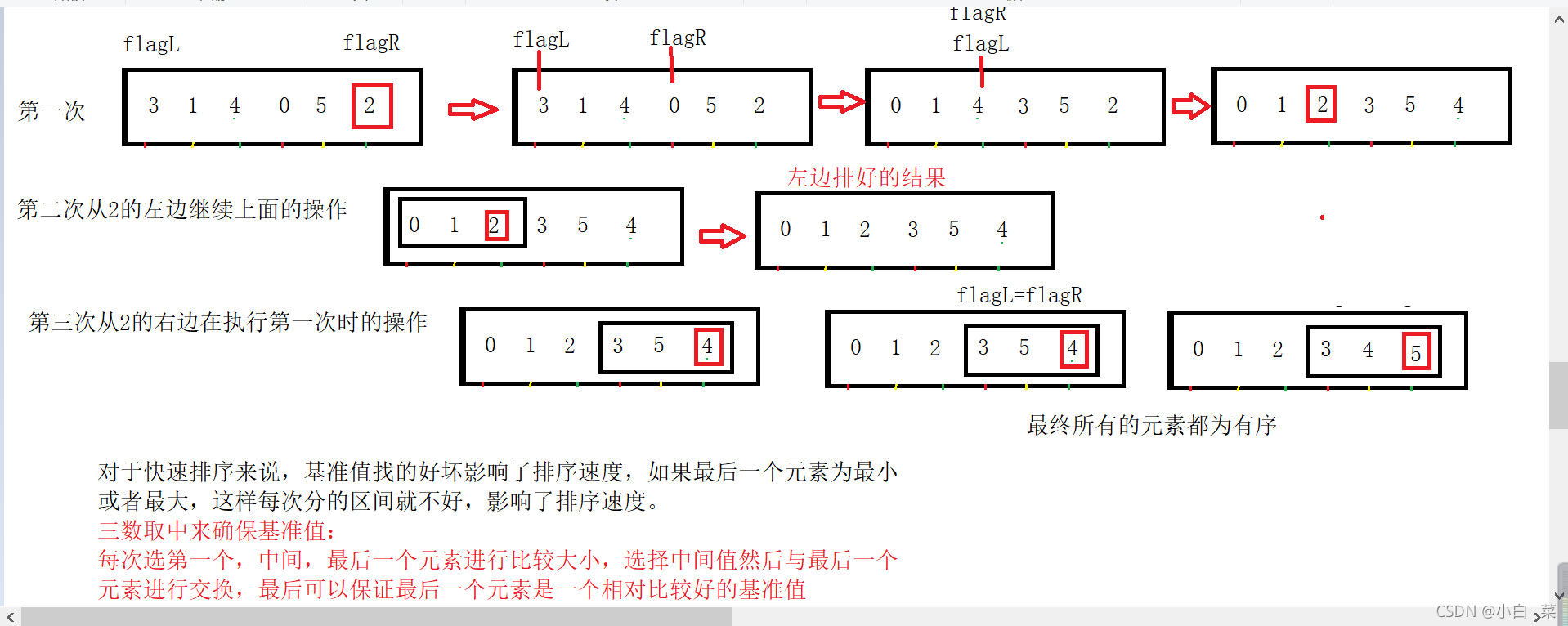
4.代码实现
如果递归深度过深，我们可以对递归到小区间的时候使用插入排序，这样可以提高排序速度，这样也是对快排进行优化。
//使用三数取中法选择合适基准值，对快排优化
public static int midDiv(int[] arr,int left,int right){
int mid = left+(right-left)>>1;
//在左右值比较后然后中间值与左右进行比较
if(arr[left]<arr[right-1]){//左小右大
if(arr[mid]<arr[left]){
return left;
}else if(arr[mid]>arr[right-1]){
return right-1;
}else{
return mid;
}
}else {//左大右小
if(arr[mid]<arr[right-1]){
return right-1;
}else if(arr[mid]>arr[left]){
return left;
}else {
return mid;
}
}
}
//前后指针法，划分区间，得到基准值
public static int partiton(int[] arr,int left,int right){
int midDiv=midDiv(arr,left,right);//找合适基准值的位置
swap(arr,midDiv,right-1);//基准值位置与最后元素交换
int begin = left;//从初始位置
int end = right-1;//末尾位置
int tmp = arr[right-1];//保存基准值
while(begin<end) {
//从前找比基准值大的元素下标
while(begin<end && arr[begin]<=tmp) {
begin++;
}
//从后找比基准值小的元素下标
while(begin<end && arr[end]>=tmp) {
end--;
}
//将找到的元素进行交换
if(begin != end){
swap(arr, begin, end);
}
}
//将中间值位置与基准值交换
if(begin != right-1){
swap(arr, begin, right-1);
}
//返回基准值的下标
return begin;
}
//交换
public void swap(int[] arr, int left, int right) {
int tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
}
//快速排序(递归版)
public static void quickSort(int[] arr,int left,int right){
//剩一个元素排序结束
if(right-left>1){
int div = partiton(arr,left,right);//找基准值划分区间
//左[left,val)
quickSort(arr,left,div);
//右[val+1,right)
quickSort(arr,div+1,right);
}5.时间复杂度，空间复杂度及稳定性分析
（1）时间复杂度
注意：对于未选择三数取中的方法时，最坏的时间复杂度为O(N^2)，这是因为可能每次划分的时候左边的都比最后一个小，相当于每次只能排好一个，每一个需要的时间大概为N,共有N个元素，所以为O(N^2)，但是当每次最后一个数都为中间值的时候，时间复杂度就变为O(*N)，为递归的深度。
通过优化后最终得到的时间复杂度为O(*N)
（2）空间复杂度
在递归的时候借助了辅助空间，空间复杂度为递归的深度，所以空间复杂度为O()。
（3）稳定性
间隔进行了交换，所以不稳定。
6.应用场景
在数据特别随机的时候使用快排比较高效
七.归并排序
1.归并思想
该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
2.归并排序动图演示
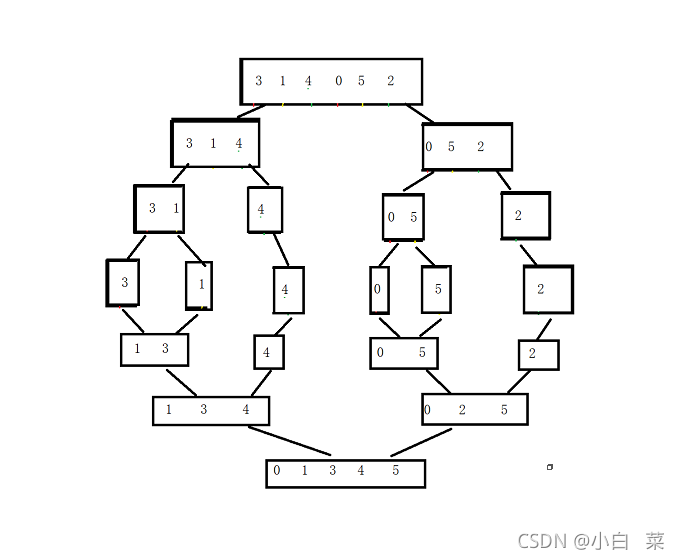
3.实现归并的思路图解
·
4.代码实现
public static void mergeSort(int[] arr,int left,int right,int[] temp){
if(right-left>1){
int mid = left+((right-left)>>1);//注意优先级问题，否则会出现栈溢出
//分区间
mergeSort(arr,left,mid,temp);
mergeSort(arr,mid,right,temp);
//（合区间）将划分好的区间进行有序合并
mergeData(arr,left,mid,right,temp);
//将合并好的区间拷贝的原数组中
System.arraycopy(temp,left,arr,left,right-left);
}
}
//负责将划分好的区间进行合并
public static void mergeData(int[] arr,int left,int mid,int right,int[] temp){
int leftT=left;
int midT = mid;
int index=left;
while(leftT<mid && midT<right){
if(arr[leftT]<=arr[midT]){
temp[index++]=arr[leftT++];
}else {
temp[index++]=arr[midT++];
}
}
while(leftT<mid){
temp[index++]=arr[leftT++];
}
while(midT<right){
temp[index++]=arr[midT++];
}
}5.时间复杂度，空间复杂度及稳定性分析
（1）时间复杂度
O(*N)
（2）空间复杂度
这里分析空间复杂度的时候不能按照递归深度*合并次数来进行计算，因为每次递归合并后，就将之前的空间释放掉了，所以借助的空间只有之前的辅助空间用来存储合并有序的数，最终空间复杂度为O(N)
（3）稳定性
在进行归并的时候没有间隔，所以稳定。
6.应用场景
应用于外部排序。
八.计数排序
1.排序思想
统计相同元素出现的次数，然后根据统计的次数回收到原来的数组中即可。
2.应用场景
对于数据特别集中在某个范围内时，效率是很高的。
3.思路图解
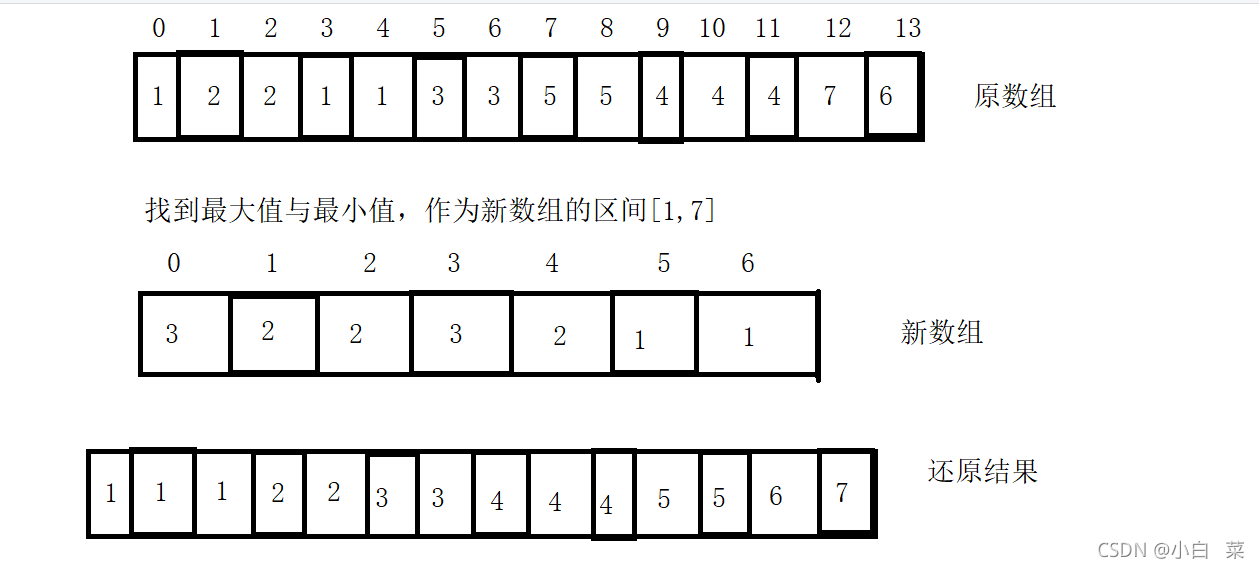
4.代码实现
public static void countSort(int[] arr){
int size=arr.length;
if(size==0){
return;
}
int max=arr[0];
int min=arr[0];
//获取最大最小值
for(int i=1;i<size;i++){
if(arr[i]>max){
max=arr[i];
}
if(arr[i]<min){
min=arr[i];
}
}
//这里数组的大小为max-min+1，直接使用max-min会出现数组越界
int[] tmp = new int[max-min+1];
//将每一个值出现的次数保存到对应的位置即可
for(int i=0;i<size;i++){
tmp[arr[i]-min]++;
}
int index=0;
//将结果进行还原
for(int i=0;i<tmp.length;i++){
for(int j=0;j<tmp[i];j++){
arr[index++]=min+i;
}
}
}5.时间复杂度，空间复杂度及稳定性
（1）时间复杂度
时间复杂度为：O(N)，为元素的个数
（2）空间复杂度
空间复杂度为：O(Max-Min)
（3）稳定性
没有间隔交换稳定
6.应用场景
对于数字比较集中在某个区间范围内时排序效率比较高。